В успоредник точката лежи на страната ,. Изразете вектора чрез векторите и .

Решение на проблема

Този урок показва как да използвате известни вектори под формата на страни на успоредник, за да изразите произволен сегмент като композиция от оригиналните вектори. Тази задачане би могло да има решение, ако не знаем в какво отношение една от страните на успоредника е разделена от точка, принадлежаща на търсената отсечка. По-нататъшните действия се свеждат до определяне на началото и края на дадените вектори и векторите, на които е разделена страната. Всичко това е необходимо за правилното използване на знаци при комбиниране на вектори. В крайна сметка е необходимо да запомните правилата за добавяне на вектори: сумата от вектори дава трети вектор, чието начало съвпада с началото на първия вектор, а краят с края на втория; и правилото за изваждане на вектори: разликата на два вектора е третият вектор, чието начало съвпада с краищата на втория вектор, а краят с края на първия вектор. Въз основа на тези прости правила можем да получим комбинацията, от която се нуждаем.

Ще има и задачи за самостоятелно решаване, на които можете да видите отговорите.

Векторна концепция

Преди да научите всичко за векторите и операциите върху тях, пригответе се да решите една проста задача. Има вектор на вашата предприемчивост и вектор на вашите иновативни способности. Векторът на предприемачеството ви води към цел 1, а векторът на иновативните способности ви води към цел 2. Правилата на играта са такива, че не можете да се движите по посоките на тези два вектора едновременно и да постигнете две цели наведнъж. Векторите си взаимодействат, или, ако кажем математически език, се извършва някаква операция върху векторите. Резултатът от тази операция е векторът „Резултат“, който ви води до цел 3.

Сега ми кажете: резултатът от коя операция върху векторите „Предприемачество” и „Иновационни способности” е векторът „Резултат”? Ако не можете да кажете веднага, не се обезсърчавайте. Докато напредвате в този урок, ще можете да отговорите на този въпрос.

Както вече видяхме по-горе, векторът задължително идва от определена точка Апо права линия до някаква точка б. Следователно всеки вектор има не само числена стойност - дължина, но и физическа и геометрична стойност - посока. Оттук идва първата, най-проста дефиниция на вектор. И така, векторът е насочен сегмент, идващ от точка Адо точката б. Означава се, както следва: .


И да започна различни операции с вектори , трябва да се запознаем с още една дефиниция на вектор.

Векторът е вид представяне на точка, която трябва да бъде достигната от някаква начална точка. Например, триизмерен вектор обикновено се записва като (x, y, z) . С много прости думи, тези числа означават колко далеч трябва да изминете в три различни посоки, за да стигнете до дадена точка.

Нека е даден вектор. В същото време х = 3 (дясната ръка сочи надясно), г = 1 (лява ръкаточки напред) z = 5 (под точката има стълба, водеща нагоре). Използвайки тези данни, ще намерите точка, като изминете 3 метра в посочената посока дясна ръка, след това 1 метър в посоката, посочена от лявата ви ръка, а след това ви очаква стълба и, издигайки се 5 метра, накрая ще се озовете в крайната точка.

Всички останали термини са пояснения на обяснението, представено по-горе, необходими за различни операции с вектори, тоест решаване на практически задачи. Нека преминем през тези по-строги дефиниции, като се фокусираме върху типичните векторни проблеми.

Физически примеривекторни величини могат да бъдат преместването на материална точка, движеща се в пространството, скоростта и ускорението на тази точка, както и силата, действаща върху нея.

Геометричен векторпредставени в двумерно и тримерно пространство във формата насочен сегмент. Това е сегмент, който има начало и край.

Ако А- началото на вектора и б- краят му, тогава векторът се обозначава със символ или един малка буква. На фигурата краят на вектора е обозначен със стрелка (фиг. 1)

Дължина(или модул) на геометричен вектор е дължината на сегмента, който го генерира

Двата вектора се наричат равен , ако могат да се комбинират (ако посоките съвпадат) от паралелен трансфер, т.е. ако са успоредни, насочени в една и съща посока и имат равни дължини.

Във физиката често се разглежда фиксирани вектори, определени от точката на приложение, дължина и посока. Ако точката на приложение на вектора няма значение, тогава той може да бъде прехвърлен, запазвайки дължината и посоката си, до всяка точка в пространството. В този случай векторът се нарича безплатно. Ще се съгласим да разгледаме само безплатни вектори.

Линейни операции върху геометрични вектори

Умножение на вектор по число

Продукт на вектор на бройе вектор, който се получава от вектор чрез разтягане (при ) или компресиране (при ) с коефициент и посоката на вектора остава същата, ако , и се променя в противоположната, ако . (фиг. 2)

От определението следва, че векторите и = винаги са разположени на една или успоредни прави. Такива вектори се наричат колинеарен. (Можем също да кажем, че тези вектори са успоредни, но във векторната алгебра е обичайно да се казва „колинеарни“.) Обратното също е вярно: ако векторите са колинеарни, тогава те са свързани с връзката

Следователно равенството (1) изразява условието за колинеарност на два вектора.


Събиране и изваждане на вектори

Когато добавяте вектори, трябва да знаете това сумавектори и се нарича вектор, чието начало съвпада с началото на вектора, а краят с края на вектора, при условие че началото на вектора е прикрепено към края на вектора. (фиг. 3)


Тази дефиниция може да бъде разпределена върху произволен краен брой вектори. Нека бъдат дадени в космоса пбезплатни вектори. При добавяне на няколко вектора тяхната сума се приема за затварящ вектор, чието начало съвпада с началото на първия вектор, а краят с края на последния вектор. Тоест, ако прикрепите началото на вектора към края на вектора и началото на вектора към края на вектора и т.н. и накрая до края на вектора - началото на вектора, тогава сумата от тези вектори е затварящият вектор , чието начало съвпада с началото на първия вектор, а краят - с края на последния вектор. (фиг. 4)

Членовете се наричат ​​компоненти на вектора, а формулираното правило е правило на многоъгълника. Този многоъгълник може да не е плосък.

Когато един вектор се умножи по числото -1, се получава противоположният вектор. Векторите и имат еднакви дължини и противоположни посоки. Сборът им дава нулев вектор, чиято дължина е нула. Посоката на нулевия вектор не е дефинирана.

Във векторната алгебра няма нужда да разглеждаме операцията за изваждане отделно: изваждането на вектор от вектор означава добавяне на противоположния вектор към вектора, т.е.

Пример 1.Опростете израза:

.

,

тоест, векторите могат да се събират и умножават по числа по същия начин като полиномите (по-специално, също и проблеми с опростяване на изрази). Обикновено необходимостта от опростяване на линейно подобни изрази с вектори възниква преди изчисляването на продуктите на векторите.

Пример 2.Вектори и служат като диагонали на успоредника ABCD (фиг. 4а). Изразете през и векторите , , и , които са страните на този успоредник.

Решение. Пресечната точка на диагоналите на успоредника разполовява всеки диагонал. Намираме дължините на векторите, изисквани в формулировката на проблема, или като половината от сумите на векторите, които образуват триъгълник с търсените, или като половината от разликите (в зависимост от посоката на вектора, служещ за диагонал), или, както в последния случай, половината от сумата, взета със знак минус. Резултатът са векторите, изисквани в изложението на проблема:

Има всички основания да вярваме, че вече сте отговорили правилно на въпроса за векторите „Предприемачество“ и „Иновативни способности“ в началото на този урок. Правилен отговор: върху тези вектори се извършва операция на добавяне.

Решете векторни задачи сами и след това разгледайте решенията

Как да намерим дължината на сумата от вектори?

Този проблем заема специално място в операциите с вектори, тъй като включва използването на тригонометрични свойства. Да приемем, че попаднете на задача като следната:

Дадени са дължините на вектора и дължината на сумата от тези вектори. Намерете дължината на разликата между тези вектори.

Решенията на този и други подобни проблеми и обяснения за решаването им са в урока " Векторно събиране: дължина на сумата от вектори и косинусова теорема ".

И можете да проверите решението на такива проблеми на Онлайн калкулатор "Неизвестна страна на триъгълник (векторно събиране и косинусова теорема)" .

Къде са продуктите на векторите?

Продуктите вектор-вектор не са линейни операции и се разглеждат отделно. И имаме уроци "Скаларно произведение на вектори" и "Векторни и смесени произведения на вектори".

Проекция на вектор върху ос

Проекцията на вектор върху ос е равна на произведението на дължината на проектирания вектор и косинуса на ъгъла между вектора и оста:

Както е известно, проекцията на точка Авърху правата линия (равнина) е основата на перпендикуляра, пуснат от тази точка върху правата линия (равнина).


Нека е произволен вектор (фиг. 5) и и са проекциите на неговия произход (точки А) и край (точки б) на ос л. (За изграждане на проекция на точка А) начертайте права линия през точката Аравнина, перпендикулярна на права линия. Пресечната точка на правата и равнината ще определи необходимата проекция.

Векторна компонента по оста lсе нарича такъв вектор, лежащ на тази ос, чието начало съвпада с проекцията на началото, а краят с проекцията на края на вектора.

Проекция на вектора върху оста лизвикан номер

,

равна на дължината на компонентния вектор на тази ос, взета със знак плюс, ако посоката на компонентите съвпада с посоката на оста л, и със знак минус, ако тези посоки са противоположни.

Основни свойства на векторните проекции върху ос:

1. Проекциите на еднакви вектори върху една и съща ос са равни една на друга.

2. Когато един вектор се умножи по число, неговата проекция се умножи по същото число.

3. Проекцията на сумата от вектори върху произволна ос е равна на сумата от проекциите на сборните на векторите върху същата ос.

4. Проекцията на вектора върху оста е равна на произведението на дължината на проектирания вектор и косинуса на ъгъла между вектора и оста:

.

Решение. Нека проектираме вектори върху оста лкакто е дефинирано в теоретичната основа по-горе. От фиг. 5а е очевидно, че проекцията на сумата от вектори е равна на сумата от проекциите на векторите. Ние изчисляваме тези прогнози:

Намираме крайната проекция на сумата от вектори:

Връзка между вектор и правоъгълна декартова координатна система в пространството

Опознаване правоъгълна декартова координатна система в пространството се проведе в съответния урок, препоръчително е да го отворите в нов прозорец.

В подредена система от координатни оси 0xyzос волнаречен ос х, ос 0 г – у-ос, и ос 0z – прилагане на ос.


С произволна точка Мкосмически свързващ вектор

наречен радиус векторточки Ми го проектираме върху всяка от координатните оси. Нека обозначим величините на съответните проекции:

Числа x, y, zсе наричат координати на точка М, съответно абсцисата, ординатаИ прилагам, и се записват като подредена точка от числа: M(x;y;z)(фиг. 6).

Нарича се вектор с единична дължина, чиято посока съвпада с посоката на оста единичен вектор(или ортом) оси. Нека означим с

Съответно единичните вектори на координатните оси вол, Ой, Оз

Теорема.Всеки вектор може да бъде разширен в единични вектори на координатни оси:


(2)

Равенството (2) се нарича разширение на вектора по координатните оси. Коефициентите на това разширение са проекциите на вектора върху координатните оси. По този начин коефициентите на разширение (2) на вектора по координатните оси са координатите на вектора.

След избор на определена координатна система в пространството, векторът и тройката от неговите координати се определят еднозначно взаимно, така че векторът може да се запише във формата

Представянията на вектора във формата (2) и (3) са идентични.

Условие за колинеарност на векторите по координати

Както вече отбелязахме, векторите се наричат ​​колинеарни, ако са свързани с релацията

Нека векторите са дадени . Тези вектори са колинеарни, ако координатите на векторите са свързани с релацията

,

тоест координатите на векторите са пропорционални.

Пример 6.Дадени са вектори . Колинеарни ли са тези вектори?

Решение. Нека разберем връзката между координатите на тези вектори:

.

Координатите на векторите са пропорционални, следователно векторите са колинеарни или, което е същото, успоредни.

Дължина на вектор и косинуси на посоката

Поради взаимната перпендикулярност на координатните оси дължината на вектора

равна на дължината на диагонала на правоъгълен паралелепипед, построен върху вектори

и се изразява с равенството

(4)

Векторът е напълно дефиниран чрез указване на две точки (начална и крайна), така че координатите на вектора могат да бъдат изразени чрез координатите на тези точки.

Нека в дадена координатна система началото на вектора е в точката

и краят е в точката


От равенството

От това следва, че

или в координатна форма

следователно координатите на вектора са равни на разликите между същите координати на края и началото на вектора . Формула (4) в този случай ще приеме формата

Определя се посоката на вектора насочващи косинуси . Това са косинусите на ъглите, които векторът сключва с осите вол, ОйИ Оз. Нека обозначим съответно тези ъгли α , β И γ . Тогава косинусите на тези ъгли могат да бъдат намерени с помощта на формулите

Насочващите косинуси на вектор са също координатите на вектора на този вектор и следователно вектора на вектора

.

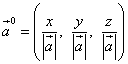
Като се има предвид, че дължината на единичния вектор е равна на една единица, т.е

,

получаваме следното равенствоза насочващи косинуси:

Пример 7.Намерете дължината на вектора х = (3; 0; 4).

Решение. Дължината на вектора е

Пример 8.Дадени точки:

Разберете дали триъгълникът, построен върху тези точки, е равнобедрен.

Решение. Използвайки формулата за дължина на вектора (6), намираме дължините на страните и определяме дали между тях има две равни:

Намерени са две равни страни, следователно няма нужда да се търси дължината на третата страна, а дадения триъгълник е равнобедрен.

Пример 9.Намерете дължината на вектора и неговите насочващи косинуси, ако .

Решение. Координатите на вектора са дадени:

.

Дължината на вектора е корен квадратенот сумата на квадратите на векторните координати:

.

Намиране на косинуси на посоката:

Решете векторната задача сами и след това вижте решението

Операции с вектори, дадени в координатна форма

Нека два вектора и са дадени, определени от техните проекции:

Нека посочим действия върху тези вектори.

Най-после се сдобих с тази обширна и дългоочаквана тема. аналитична геометрия. Първо, малко за този раздел на висшата математика... Със сигурност си спомняте училищен курс по геометрия с множество теореми, техните доказателства, чертежи и т.н. Какво да крия, нелюбим и често неясен предмет за значителна част от учениците. Колкото и да е странно, аналитичната геометрия може да изглежда по-интересна и достъпна. Какво означава прилагателното „аналитичен“? Две клиширани математически фрази веднага идват на ум: „метод на графично решение“ и „метод на аналитично решение“. Графичен метод , разбира се, е свързано с изграждането на графики и чертежи. Аналитиченсъщото методвключва решаване на проблеми главночрез алгебрични операции. В това отношение алгоритъмът за решаване на почти всички проблеми на аналитичната геометрия е прост и прозрачен, често е достатъчно внимателно да се прилага необходимите формули- и отговорът е готов! Не, разбира се, няма да можем да направим това без рисунки и освен това, за по-добро разбиране на материала, ще се опитам да ги цитирам извън необходимостта.

Новооткритият курс от уроци по геометрия не претендира да бъде теоретично завършен; той е насочен към решаване на практически задачи. В моите лекции ще включвам само това, което от моя гледна точка е важно в практически план. Ако имате нужда от по-пълна помощ за някой подраздел, препоръчвам следната доста достъпна литература:

1) Нещо, с което, без шега, са запознати няколко поколения: Училищен учебник по геометрия, автори – Л.С. Атанасян и компания. Тази закачалка за училищна съблекалня вече е преминала през 20 (!) Препечатки, което, разбира се, не е ограничението.

2) Геометрия в 2 тома. автори Л.С. Атанасян, Базилев В.Т.. Това е литература за гимназия, ще ви трябва първи том. Рядко срещаните задачи могат да изпаднат от погледа ми и наръчник за обучениеще окаже безценна помощ.

И двете книги могат да бъдат изтеглени безплатно онлайн. Освен това можете да използвате моя архив с готови решения, които можете да намерите на страницата Изтегляне на примери по висша математика .

Сред инструментите отново предлагам собствена разработка - софтуерен пакет в аналитичната геометрия, което значително ще опрости живота и ще спести много време.

Предполага се, че читателят е запознат с основните геометрични понятия и фигури: точка, права, равнина, триъгълник, паралелограм, паралелепипед, куб и др. Препоръчително е да запомните някои теореми, поне теоремата на Питагор, здравейте на повторителите)

И сега ще разгледаме последователно: понятието вектор, действия с вектори, векторни координати. Препоръчвам да прочетете допълнително най-важната статия Точково произведение на вектори , а също така Вектор и смесено произведение на вектори . Местна задача няма да е излишна - Разделяне на сегмент в това отношение. Въз основа на горната информация можете да овладеете уравнение на права в равнина с най-прости примери за решения , което ще позволи научете се да решавате геометрични задачи . Следните статии също са полезни: Уравнение на равнина в пространството , Уравнения на права в пространството , Основни задачи по прави и равнини, други клонове на аналитичната геометрия. Естествено, стандартните задачи ще бъдат разгледани по пътя.

Векторна концепция. Безплатен вектор

Първо, нека повторим училищната дефиниция на вектор. векторнаречен насоченисегмент, за който са посочени неговото начало и край:

В този случай началото на сегмента е точката, краят на сегмента е точката. Самият вектор се означава с . Посокае от съществено значение, ако преместите стрелката в другия край на сегмента, получавате вектор и това вече е напълно различен вектор. Концепцията за вектор е удобно идентифицирана с движение физическо тяло: Съгласете се, влизането през вратите на института или излизането от вратите на института са съвсем различни неща.

Удобно е отделни точки от една равнина или пространство да се разглеждат като т.нар нулев вектор. За такъв вектор краят и началото съвпадат.

!!! Забележка: Тук и по-нататък можете да приемете, че векторите лежат в една равнина или можете да приемете, че са разположени в пространството - същността на изложения материал е валидна както за равнината, така и за пространството.

Обозначения:Мнозина веднага забелязаха пръчката без стрелка в обозначението и казаха, че има и стрелка в горната част! Вярно, че можете да го напишете със стрелка: , но и това е възможно записът, който ще използвам в бъдеще. защо Очевидно този навик се е развил по практически причини; стрелците ми в училище и университета се оказаха твърде различни по размер и рошави. В образователната литература понякога те изобщо не се занимават с клинописно писане, а подчертават буквите с удебелен шрифт: , като по този начин намекват, че това е вектор.

Това беше стилистика, а сега относно начините за писане на вектори:

1) Векторите могат да бъдат написани с две главни латински букви:
и така нататък. В този случай първата буква Задължителнообозначава началната точка на вектора, а втората буква обозначава крайната точка на вектора.

2) Векторите също се изписват с малки латински букви:
По-специално, за краткост нашият вектор може да бъде преозначен като малък латиница.

Дължинаили модулненулев вектор се нарича дължина на сегмента. Дължината на нулевия вектор е нула. Логично.

Дължината на вектора се обозначава със знака за модул: ,

Ще научим как да намираме дължината на вектор (или ще го повторим, зависи кой) малко по-късно.

Това беше основна информация за векторите, позната на всички ученици. В аналитичната геометрия т.нар безплатен вектор.

Казано по-просто - векторът може да се начертае от всяка точка:

Ние сме свикнали да наричаме такива вектори равни (дефиницията на равни вектори ще бъде дадена по-долу), но от чисто математическа гледна точка те са ЕДИН И СЪЩ ВЕКТОР или безплатен вектор. Защо безплатно? Защото в хода на решаване на проблеми можете да „прикрепите“ този или онзи „училищен“ вектор към ВСЯКА точка от равнината или пространството, от което се нуждаете. Това е много готина функция! Представете си насочен сегмент с произволна дължина и посока - той може да бъде "клониран" безкраен брой пъти и във всяка точка на пространството, всъщност той съществува НАВСЯКЪДЕ. Има една студентска поговорка: На всеки преподавател му пука за вектора. В крайна сметка това не е просто остроумна рима, всичко е почти правилно - там може да се добави и насочен сегмент. Но не бързайте да се радвате, често страдат самите ученици =)

така че безплатен вектор- Това много еднакви насочени сегменти. Определение за училищевектор, даден в началото на параграфа: „Насочен сегмент се нарича вектор...“ предполага специфиченнасочен сегмент, взет от дадено множество, който е свързан с определена точка в равнината или пространството.

Трябва да се отбележи, че от гледна точка на физиката концепцията за свободен вектор в общ случайе неправилно и има значение точката на приложение. Наистина, директен удар с еднаква сила по носа или челото, достатъчен, за да развия моя глупав пример, води до различни последствия. обаче несвободенвектори срещами вие сте наясно с vyshmat (не отивайте там :)).

Действия с вектори. Колинеарност на вектори

Училищният курс по геометрия обхваща редица действия и правила с вектори: събиране по правилото на триъгълника, събиране по правилото на успоредника, правило за векторна разлика, умножение на вектор с число, скаларно произведение на вектори и др.Като отправна точка нека повторим две правила, които са особено подходящи за решаване на задачи от аналитичната геометрия.

Правилото за добавяне на вектори с помощта на правилото на триъгълника

Помислете за два произволни ненулеви вектора и:

Трябва да намерите сумата от тези вектори. Поради факта, че всички вектори се считат за свободни, ще отделим вектора от крайвектор:

Сумата от вектори е векторът. За по-добро разбиране на правилото е препоръчително да включите физически смисъл: нека някакво тяло пътува по вектор, а след това по вектор. Тогава сумата от вектори е векторът на резултантния път с начало в началната точка и край в точката на пристигане. Подобно правило е формулирано за сумата от произволен брой вектори. Както се казва, тялото може да върви по своя път много постно по зигзаг или може би на автопилот - по резултантния вектор на сумата.

Между другото, ако векторът е отложен от започнавектор, тогава получаваме еквивалента правило на успоредникдобавяне на вектори.

Първо, относно колинеарността на векторите. Двата вектора се наричат колинеарен, ако лежат на една права или на успоредни прави. Грубо казано, говорим за паралелни вектори. Но по отношение на тях винаги се използва прилагателното „колинеарни“.

Представете си два колинеарни вектора. Ако стрелките на тези вектори са насочени в една и съща посока, тогава такива вектори се наричат съвместно режисиран. Ако стрелките сочат в различни посоки, тогава векторите ще бъдат противоположни посоки.

Обозначения:колинеарността на векторите се записва с обичайния символ за паралелизъм: , докато е възможно детайлизиране: (векторите са сънасочени) или (векторите са противоположно насочени).

Работатаненулев вектор върху число е вектор, чиято дължина е равна на , а векторите и са сънасочени към и противоположно насочени към .

Правилото за умножаване на вектор по число е по-лесно за разбиране с помощта на картина:

Нека го разгледаме по-подробно:

1) Посока. Ако множителят е отрицателен, тогава векторът променя посокатакъм обратното.

2) Дължина. Ако множителят се съдържа в или , тогава дължината на вектора намалява. Така дължината на вектора е половината от дължината на вектора. Ако модулът на множителя е по-голям от едно, тогава дължината на вектора увеличавана моменти.

3) Моля, имайте предвид, че всички вектори са колинеарни, докато един вектор се изразява чрез друг, например, . Обратното също е вярно: ако един вектор може да бъде изразен чрез друг, тогава такива вектори задължително са колинеарни. Така: ако умножим вектор по число, получаваме колинеарни(спрямо оригинала) вектор.

4) Векторите са ко-насочени. Вектори и също са съвместно насочени. Всеки вектор от първата група е противоположно насочен по отношение на всеки вектор от втората група.

Кои вектори са равни?

Два вектора са равни, ако са в една и съща посока и имат еднаква дължина. Обърнете внимание, че една насоченост предполага колинеарност на векторите. Определението би било неточно (излишно), ако кажем: „Два вектора са равни, ако са колинеарни, еднакви по посока и имат еднаква дължина.“

От гледна точка на концепцията за свободен вектор, равните вектори са един и същ вектор, както беше обсъдено в предишния параграф.

Векторни координати в равнината и пространството

Първата точка е да разгледаме векторите в равнината. Нека да изобразим декартова правоъгълна координатна система и да я начертаем от началото на координатите единиченвектори и:

Вектори и ортогонален. Ортогонално = Перпендикулярно. Препоръчвам ви бавно да свикнете с термините: вместо успоредност и перпендикулярност използваме думите съответно колинеарностИ ортогоналност.

Обозначение:Ортогоналността на векторите се записва с обичайния символ за перпендикулярност, например: .

Разглежданите вектори се наричат координатни векториили orts. Тези вектори образуват основав самолет. Какво е основа, мисля, че е интуитивно ясно за мнозина, повече подробна информацияможете да намерите в статията Линейна (не)зависимост на векторите. Основа на векторите С прости думи, основата и произходът на координатите определят цялата система - това е един вид основа, върху която кипи пълен и богат геометричен живот.

Понякога изградената основа се нарича ортонормалнаоснова на равнината: “орто” - тъй като координатните вектори са ортогонални, прилагателното “нормализиран” означава единица, т.е. дължините на базисните вектори са равни на единица.

Обозначение:основата обикновено се изписва в скоби, вътре в които в строга последователностбазисните вектори са изброени, например: . Координатни вектори забранено епренареждам.

Всякаквиравнинен вектор единственият начинизразено като:
, къде - числакоито се наричат векторни координатив тази основа. И самият израз наречен векторно разлаганепо основа .

Сервирана вечеря:

Да започнем с първата буква от азбуката: . Чертежът ясно показва, че при разлагането на вектор в базис се използват току-що обсъдените:
1) правилото за умножаване на вектор с число: и ;
2) събиране на вектори по правилото на триъгълника: .

Сега мислено начертайте вектора от всяка друга точка на равнината. Съвсем очевидно е, че неговото упадък ще го „следва безмилостно“. Ето я свободата на вектора - векторът „носи всичко със себе си“. Това свойство, разбира се, е вярно за всеки вектор. Забавно е, че самите базисни (свободни) вектори не трябва да се изчертават от началото; Вярно е, че не е нужно да правите това, тъй като учителят също ще покаже оригиналност и ще ви изтегли „кредит“ на неочаквано място.

Векторите илюстрират точно правилото за умножение на вектор по число, векторът е съпосочен с основния вектор, векторът е насочен срещуположно на основния вектор. За тези вектори една от координатите е равна на нула, можете да го запишете така:


А базисните вектори, между другото, са така: (всъщност те се изразяват чрез себе си).

И накрая: , . Между другото, какво е векторно изваждане и защо не говорих за правилото за изваждане? Някъде в линейната алгебра, не помня къде, отбелязах, че изваждането е специален случайдопълнение. По този начин разширенията на векторите "de" и "e" лесно се записват като сума: , . Следвайте чертежа, за да видите колко ясно работи доброто старо добавяне на вектори според правилото на триъгълника в тези ситуации.

Разгледаното разлагане на формата понякога се нарича векторно разлагане в орт системата(т.е. в система от единични вектори). Но това не е единственият начин да напишете вектор;

Или със знак за равенство:

Самите базисни вектори се записват по следния начин: и

Тоест координатите на вектора са посочени в скоби. В практически задачи се използват и трите варианта на нотация.

Съмнявах се дали да говоря, но все пак ще го кажа: векторните координати не могат да бъдат пренареждани. Строго на първо мястозапишете съответната координата единичен вектор , строго на второ мястозаписваме координатата, която съответства на единичния вектор. Наистина и са два различни вектора.

Намерихме координатите на самолета. Сега нека да разгледаме векторите в триизмерното пространство, тук почти всичко е същото! Просто ще добави още една координата. Трудно е да се правят триизмерни рисунки, така че ще се огранича до един вектор, който за простота ще отделя от началото:

Всякакви 3D космически вектор единственият начин разширяване върху ортонормална основа:
, където са координатите на вектора (числото) в тази основа.

Пример от снимката: . Нека видим как работят векторните правила тук. Първо, умножете вектора по число: (червена стрелка), (зелена стрелка) и (малинова стрелка). Второ, ето пример за добавяне на няколко в това случай от три, вектори: . Векторът на сумата започва от началната точка на изход (началото на вектора) и завършва в крайната точка на пристигане (края на вектора).

Всички вектори на триизмерното пространство, естествено, също са свободни; опитайте се мислено да отделите вектора от всяка друга точка и ще разберете, че неговото разлагане „ще остане с него“.

Подобно на плоския случай, в допълнение към писането широко се използват варианти със скоби: или .

Ако един (или два) координатни вектора липсват в разширението, тогава на тяхно място се поставят нули. Примери:
вектор (щателно ) – да пишем ;
вектор (щателно) – запишете;
вектор (щателно ) – да пишем.

Базисните вектори се записват, както следва:

Това може би са всички минимални теоретични познания, необходими за решаване на проблемите на аналитичната геометрия. Може да има много термини и определения, така че препоръчвам на чайниците да препрочетат и разберат тази информация отново. И ще бъде полезно за всеки читател да се обърне към него основен урокза по-добро усвояване на материала. Колинеарност, ортогоналност, ортонормална основа, векторно разлагане - тези и други понятия ще бъдат често използвани в бъдеще. Отбелязвам, че материалите на сайта не са достатъчни за преминаване на теоретичния тест или колоквиума по геометрия, тъй като аз внимателно криптирам всички теореми (и без доказателства) - в ущърб на научния стил на представяне, но плюс за вашето разбиране на темата. За да получите подробна теоретична информация, моля да се поклоните на проф. Атанасян.

И преминаваме към практическата част:

Най-простите задачи на аналитичната геометрия.
Действия с вектори в координати

Силно препоръчително е да научите как да решавате задачите, които ще се разглеждат напълно автоматично, и формулите запаметявам, дори не е нужно да го помните нарочно, те сами ще го запомнят =) Това е много важно, тъй като други проблеми на аналитичната геометрия се основават на най-простите елементарни примери и ще бъде досадно да прекарвате допълнително време в ядене на пешки . Няма нужда да закопчавате горните копчета на ризата, много неща са ви познати от училище.

Поднасянето на материала ще следва паралелен ход – както за самолета, така и за космоса. Поради причината, че всички формули... ще видите сами.

Как да намерим вектор от две точки?

Ако са дадени две точки от равнината и , тогава векторът има следните координати:

Ако са дадени две точки в пространството и , тогава векторът има следните координати:

т.е. от координатите на края на векторатрябва да извадите съответните координати началото на вектора.

Упражнение:За същите точки запишете формулите за намиране на координатите на вектора. Формули в края на урока.

Пример 1

Дадени са две точки от равнината и . Намерете векторни координати

Решение:по съответната формула:

Като алтернатива може да се използва следният запис:

Естетите ще решат това:

Лично аз съм свикнал с първия вариант на записа.

отговор:

Според условието не беше необходимо да се изгражда чертеж (което е типично за проблемите на аналитичната геометрия), но за да изясня някои точки за манекени, няма да бъда мързелив:

Определено трябва да разберете разлика между координатите на точката и векторните координати:

Координати на точки– това са обикновени координати в правоъгълна координатна система. Мисля, че всеки знае как се нанасят точки върху координатна равнина от 5-6 клас. Всяка точка има строго определено място в равнината и не може да бъде преместена никъде.

Координатите на вектора– това е разширяването му според основата, в случая. Всеки вектор е свободен, така че при желание или необходимост можем лесно да го отдалечим от някоя друга точка на равнината. Интересно е, че за векторите изобщо не е нужно да изграждате оси или правоъгълна координатна система; имате нужда само от основа, в този случай ортонормална основа на равнината.

Записите на координати на точки и координати на вектори изглеждат подобни: , и значение на координатитеабсолютно различни, и трябва да сте добре запознати с тази разлика. Тази разлика, разбира се, важи и за пространството.

Дами и господа, нека напълним ръцете си:

Пример 2

а) Дадени са точки и . Намерете вектори и .
б) Дават се точки И . Намерете вектори и .
в) Дадени са точки и . Намерете вектори и .
г) Дават се точки. Намерете вектори .

Може би това е достатъчно. Това са примери, които можете да решите сами, опитайте се да не ги пренебрегвате, ще ви се отплати ;-). Няма нужда да правите чертежи. Решения и отговори в края на урока.

Какво е важно при решаването на задачи по аналитична геометрия?Важно е да бъдете ИЗКЛЮЧИТЕЛНО ВНИМАТЕЛНИ, за да избегнете майсторската грешка „две плюс две е равно на нула“. Веднага се извинявам, ако съм сбъркал някъде =)

Как да намерим дължината на сегмент?

Дължината, както вече беше отбелязано, се обозначава със знака за модул.

Ако са дадени две точки от равнината и , тогава дължината на сегмента може да се изчисли с помощта на формулата

Ако са дадени две точки в пространството и , тогава дължината на сегмента може да се изчисли с помощта на формулата

Забележка: Формулите ще останат правилни, ако съответните координати се разменят: и , но първата опция е по-стандартна

Пример 3

Решение:по съответната формула:

отговор:

За по-голяма яснота ще направя чертеж

сегмент – това не е вектори, разбира се, не можете да го преместите никъде. Освен това, ако рисувате в мащаб: 1 единица. = 1 см (две клетки от тетрадка), тогава полученият отговор може да се провери с обикновена линийка чрез директно измерване на дължината на отсечката.

Да, решението е кратко, но в него има още няколко важни точкикоето бих искал да изясня:

Първо, в отговора поставяме измерението: „единици“. В условието не пише КАКВО е, милиметри, сантиметри, метри или километри. Следователно, математически правилното решение би било общата формулировка: „единици“ - съкратено като „единици“.

Второ, нека повторим училищен материал, което е полезно не само за разглеждания проблем:

Моля, обърнете внимание важно техническа техника – премахване на множителя изпод корена. В резултат на изчисленията имаме резултат и добрият математически стил включва премахване на фактора под корена (ако е възможно). По-подробно процесът изглежда така: . Разбира се, да оставим отговора такъв, какъвто е, няма да е грешка - но със сигурност би било недостатък и сериозен аргумент за заяждане от страна на учителя.

Ето и други често срещани случаи:

Често коренът произвежда доста голям брой, например . Какво да правим в такива случаи? С помощта на калкулатора проверяваме дали числото се дели на 4: . Да, беше напълно разделено, така че: . Или може би числото отново може да се раздели на 4? . Така: . Последната цифра на числото е нечетна, така че разделянето на 4 за трети път очевидно няма да работи. Нека се опитаме да разделим на девет: . В резултат на това:
Готови.

Заключение:ако под корена получим число, което не може да бъде извлечено като цяло, тогава се опитваме да премахнем фактора от под корена - с помощта на калкулатор проверяваме дали числото се дели на: 4, 9, 16, 25, 36, 49 и др.

По време на решението различни задачикорените са често срещани, винаги се опитвайте да извличате фактори от корена, за да избегнете по-ниска оценка и ненужни проблеми с финализирането на вашите решения въз основа на коментарите на учителя.

Нека също повторим корени на квадрат и други степени:

Правила за действия със степени в общ изгледможе да се намери в училищен учебникпо алгебра, но мисля, че от дадените примери вече всичко или почти всичко е ясно.

Задача за самостоятелно решение с отсечка в пространството:

Пример 4

Дават се точки и . Намерете дължината на отсечката.

Решението и отговорът са в края на урока.

Как да намерим дължината на вектор?

Ако е даден плосък вектор, тогава неговата дължина се изчислява по формулата.

Ако е даден пространствен вектор, тогава неговата дължина се изчислява по формулата .