
Точката е локална максимална точка. Екстремуми, най-големи и най-малки стойности на функции
Промяната във функция в определена точка се дефинира като границата на увеличението на функцията спрямо увеличението на аргумента, което клони към нула. За да го намерите, използвайте таблицата с производни. Например, производната на функцията y = x3 ще бъде равна на y’ = x2.
Приравнете тази производна на нула (в този случай x2=0).
Намерете стойността на дадената променлива. Това ще бъдат стойностите, при които дадената производна ще бъде равна на 0. За да направите това, заместете произволни числа в израза вместо x, при което целият израз ще стане нула. Например:
2-2x2= 0
(1-x)(1+x) = 0
x1= 1, x2 = -1
Нанесете получените стойности върху координатната линия и изчислете знака на производната за всяка от получените стойности. На координатната права се отбелязват точки, които се приемат за начало. За да изчислите стойността в интервалите, заменете произволни стойности, които отговарят на критериите. Например за предишната функция преди интервала -1 можете да изберете стойност -2. За стойности от -1 до 1 можете да изберете 0, а за стойности, по-големи от 1, изберете 2. Заменете тези числа в производната и разберете знака на производната. В този случай производната с x = -2 ще бъде равна на -0,24, т.е. отрицателен и ще има знак минус на този интервал. Ако x=0, тогава стойността ще бъде равна на 2 и върху този интервал се поставя знак. Ако x=1, тогава производната също ще бъде равна на -0,24 и се поставя минус.
Ако при преминаване през точка на координатната линия производната промени знака си от минус на плюс, тогава това е минимална точка, а ако от плюс на минус, това е максимална точка.
Видео по темата
За да намерите производната, има онлайн услуги, които изчисляват необходимите стойности и показват резултата. На такива сайтове можете да намерите производни до 5-ти ред.
източници:
- Една от услугите за изчисляване на деривати
- максимална точка на функцията
Максималните точки на функция, заедно с минималните точки, се наричат точки на екстремум. В тези точки функцията променя поведението си. Екстремумите се определят на ограничени числови интервали и винаги са локални.
Инструкции
Процесът на намиране на локални екстремуми се нарича функция и се извършва чрез анализ на първата и втората производни на функцията. Преди да започнете проучването, уверете се, че зададеният диапазон от стойности на аргументи принадлежи към валидните стойности. Например за функцията F=1/x аргументът x=0 не е валиден. Или за функцията Y=tg(x) аргументът не може да има стойност x=90°.
Уверете се, че функцията Y е диференцируема в целия даден интервал. Намерете първата производна на Y." Очевидно, преди да достигне точката на локалния максимум, функцията расте, а когато премине през максимума, функцията става намаляваща. Първата производна в своята физически смисълхарактеризира скоростта на промяна на функцията. Докато функцията се увеличава, скоростта на този процес е положителна. При преминаване през локален максимум функцията започва да намалява и скоростта на изменение на функцията става отрицателна. Преходът на скоростта на изменение на функцията през нула става в точката на локалния максимум.
$E \подмножество \mathbb(R)^(n)$. Казват, че $f$ има локален максимумв точката $x_(0) \in E$, ако има околност $U$ на точката $x_(0)$ такава, че за всички $x \in U$ неравенството $f\left(x\right ) \leqslant f е изпълнено \left(x_(0)\right)$.
Локалният максимум се нарича строг , ако околността $U$ може да бъде избрана така, че за всички $x \in U$, различни от $x_(0)$, да има $f\left(x\right)< f\left(x_{0}\right)$.
Определение
Нека $f$ е реална функция в отвореното множество $E \subset \mathbb(R)^(n)$. Казват, че $f$ има местен минимумв точката $x_(0) \in E$, ако има околност $U$ на точката $x_(0)$ такава, че за всички $x \in U$ неравенството $f\left(x\right ) \geqslant f \left(x_(0)\right)$.
Локален минимум се нарича строг, ако квартал $U$ може да бъде избран така, че за всички $x \in U$, различни от $x_(0)$, да има $f\left(x\right) > f\left(x_ ( 0)\вдясно)$.
Локалният екстремум съчетава понятията локален минимум и локален максимум.
теорема ( необходимо условиеекстремум на диференцируемата функция)
Нека $f$ е реална функция в отвореното множество $E \subset \mathbb(R)^(n)$. Ако в точката $x_(0) \in E$ функцията $f$ има локален екстремум в тази точка, тогава $$\text(d)f\left(x_(0)\right)=0.$$ Равен на нула диференциал е еквивалентен на факта, че всички са равни на нула, т.е. $$\displaystyle\frac(\partial f)(\partial x_(i))\left(x_(0)\right)=0.$$
В едномерния случай това е – . Нека обозначим $\phi \left(t\right) = f \left(x_(0)+th\right)$, където $h$ е произволен вектор. Функцията $\phi$ е дефинирана за стойности на $t$, които са достатъчно малки по абсолютна стойност. В допълнение, той е диференцируем по отношение на и $(\phi)’ \left(t\right) = \text(d)f \left(x_(0)+th\right)h$.
Нека $f$ има локален максимум в точка x $0$. Това означава, че функцията $\phi$ при $t = 0$ има локален максимум и според теоремата на Ферма $(\phi)' \left(0\right)=0$.
И така, получихме, че $df \left(x_(0)\right) = 0$, т.е. функция $f$ в точка $x_(0)$ е равна на нула върху всеки вектор $h$.
Определение
Точки, в които диференциалът е нула, т.е. тези, при които всички частни производни са равни на нула, се наричат стационарни. Критични точкифункции $f$ са тези точки, в които $f$ не е диференцируемо или е равно на нула. Ако точката е неподвижна, тогава от това не следва, че функцията има екстремум в тази точка.
Пример 1.
Нека $f \left(x,y\right)=x^(3)+y^(3)$. Тогава $\displaystyle\frac(\partial f)(\partial x) = 3 \cdot x^(2)$,$\displaystyle\frac(\partial f)(\partial y) = 3 \cdot y^(2 )$, така че $\left(0,0\right)$ е стационарна точка, но функцията няма екстремум в тази точка. Наистина, $f \left(0,0\right) = 0$, но е лесно да се види, че във всяка околност на точката $\left(0,0\right)$ функцията приема както положителни, така и отрицателни стойности.
Пример 2.
Функцията $f \left(x,y\right) = x^(2) − y^(2)$ има стационарна точка в началото си, но е ясно, че в тази точка няма екстремум.
Теорема (достатъчно условие за екстремум).
Нека функцията $f$ е два пъти непрекъснато диференцируема върху отвореното множество $E \subset \mathbb(R)^(n)$. Нека $x_(0) \in E$ е неподвижна точка и $$\displaystyle Q_(x_(0)) \left(h\right) \equiv \sum_(i=1)^n \sum_(j=1 ) ^n \frac(\partial^(2) f)(\partial x_(i) \partial x_(j)) \left(x_(0)\right)h^(i)h^(j).$ $ Тогава
- ако $Q_(x_(0))$ – , тогава функцията $f$ в точката $x_(0)$ има локален екстремум, а именно минимум, ако формата е положително определена, и максимум, ако формата е отрицателно определено;
- ако квадратичната форма $Q_(x_(0))$ е недефинирана, тогава функцията $f$ в точката $x_(0)$ няма екстремум.
Нека използваме разширението по формулата на Тейлър (12.7 стр. 292). Като се има предвид, че частичните производни от първи ред в точката $x_(0)$ са равни на нула, получаваме $$\displaystyle f \left(x_(0)+h\right)−f \left(x_(0)\ дясно) = \ frac(1)(2) \sum_(i=1)^n \sum_(j=1)^n \frac(\partial^(2) f)(\partial x_(i) \partial x_ (j)) \left(x_(0)+\theta h\right)h^(i)h^(j),$$ където $0<\theta<1$. Обозначим $\displaystyle a_{ij}=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right)$. В силу теоремы Шварца (12.6 стр. 289-290) , $a_{ij}=a_{ji}$. Обозначим $$\displaystyle \alpha_{ij} \left(h\right)=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}+\theta h\right)−\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right).$$ По предположению, все непрерывны и поэтому $$\lim_{h \rightarrow 0} \alpha_{ij} \left(h\right)=0. \left(1\right)$$ Получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left.$$ Обозначим $$\displaystyle \epsilon \left(h\right)=\frac{1}{|h|^{2}}\sum_{i=1}^n \sum_{j=1}^n \alpha_{ij} \left(h\right)h_{i}h_{j}.$$ Тогда $$|\epsilon \left(h\right)| \leq \sum_{i=1}^n \sum_{j=1}^n |\alpha_{ij} \left(h\right)|$$ и, в силу соотношения $\left(1\right)$, имеем $\epsilon \left(h\right) \rightarrow 0$ при $h \rightarrow 0$. Окончательно получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left. \left(2\right)$$ Предположим, что $Q_{x_{0}}$ – положительноопределенная форма. Согласно лемме о положительноопределённой квадратичной форме (12.8.1 стр. 295, Лемма 1) , существует такое положительное число $\lambda$, что $Q_{x_{0}} \left(h\right) \geqslant \lambda|h|^{2}$ при любом $h$. Поэтому $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right) \geq \frac{1}{2}|h|^{2} \left(λ+\epsilon \left(h\right)\right).$$ Так как $\lambda>0$ и $\epsilon \left(h\right) \rightarrow 0$ за $h \rightarrow 0$, тогава дясната страна ще бъде положителна за всеки вектор $h$ с достатъчно малка дължина.
И така, стигнахме до заключението, че в някаква околност на точката $x_(0)$ неравенството $f \left(x\right) >f \left(x_(0)\right)$ е в сила, ако само $ x \neq x_ (0)$ (поставяме $x=x_(0)+h$\right). Това означава, че в точката $x_(0)$ функцията има строг локален минимум и по този начин първата част от нашата теорема е доказана.
Нека сега приемем, че $Q_(x_(0))$ е неопределена форма. Тогава има вектори $h_(1)$, $h_(2)$, така че $Q_(x_(0)) \left(h_(1)\right)=\lambda_(1)>0$, $Q_ ( x_(0)) \left(h_(2)\right)= \lambda_(2)<0$. В соотношении $\left(2\right)$ $h=th_{1}$ $t>$0. Тогава получаваме $$f \left(x_(0)+th_(1)\right)−f \left(x_(0)\right) = \frac(1)(2) \left[ t^(2) \ lambda_(1) + t^(2) |h_(1)|^(2) \epsilon \left(th_(1)\right) \right] = \frac(1)(2) t^(2) \ left[ \lambda_(1) + |h_(1)|^(2) \epsilon \left(th_(1)\right) \right].$$ За достатъчно малък $t>0$, дясната страна е положителна. Това означава, че във всяка близост на точката $x_(0)$ функцията $f$ приема стойности $f \left(x\right)$, по-големи от $f \left(x_(0)\right)$.
По същия начин откриваме, че във всяка околност на точката $x_(0)$ функцията $f$ приема стойности, по-малки от $f \left(x_(0)\right)$. Това заедно с предходното означава, че в точката $x_(0)$ функцията $f$ няма екстремум.
Нека помислим специален случайот тази теорема за функция $f \left(x,y\right)$ от две променливи, дефинирани в определена околност на точката $\left(x_(0),y_(0)\right)$ и имаща непрекъснат частичен производни на първия в този квартал и втория ред. Да приемем, че $\left(x_(0),y_(0)\right)$ е стационарна точка и обозначаваме $$\displaystyle a_(11)= \frac(\partial^(2) f)(\partial x ^ (2)) \left(x_(0) ,y_(0)\right), a_(12)=\frac(\partial^(2) f)(\partial x \partial y) \left(x_( 0) ), y_(0)\right), a_(22)=\frac(\partial^(2) f)(\partial y^(2)) \left(x_(0), y_(0)\right ) .$$ Тогава предишната теорема приема следната форма.
Теорема
Нека $\Delta=a_(11) \cdot a_(22) − a_(12)^2$. След това:
- ако $\Delta>0$, тогава функцията $f$ има локален екстремум в точката $\left(x_(0),y_(0)\right)$, а именно минимум, ако $a_(11)> 0$ и максимум, ако $a_(11)<0$;
- ако $\Delta<0$, то экстремума в точке $\left(x_{0},y_{0}\right)$ нет. Как и в одномерном случае, при $\Delta=0$ экстремум может быть, а может и не быть.
Примери за решаване на проблеми
Алгоритъм за намиране на екстремума на функция на много променливи:
- Намиране на стационарни точки;
- Намерете диференциала от 2-ри ред във всички неподвижни точки
- Използвайки достатъчното условие за екстремума на функция от много променливи, ние разглеждаме диференциала от 2-ри ред във всяка стационарна точка
- Изследвайте функцията за екстремум $f \left(x,y\right) = x^(3) + 8 \cdot y^(3) + 18 \cdot x — 30 \cdot y$.
РешениеНека намерим частичните производни от 1-ви ред: $$\displaystyle \frac(\partial f)(\partial x)=3 \cdot x^(2) - 6 \cdot y;$$ $$\displaystyle \frac(\partial f)(\partial y)=24 \cdot y^(2) - 6 \cdot x.$$ Нека съставим и решим системата: $$\displaystyle \begin(cases)\frac(\partial f)(\partial x) = 0\\\frac(\partial f)(\partial y)= 0\end(cases) \Rightarrow \begin(cases)3 \cdot x^(2) - 6 \cdot y= 0\\24 \cdot y^(2) — 6 \cdot x = 0\end(cases) \Rightarrow \begin(cases)x^(2) — 2 \cdot y= 0\\4 \cdot y^(2) — x = 0 \end(cases)$$ От второто уравнение изразяваме $x=4 \cdot y^(2)$ - заместваме го в първото уравнение: $$\displaystyle \left(4 \cdot y^(2) \right )^(2)-2 \cdot y=0$$ $$16 \cdot y^(4) — 2 \cdot y = 0$$ $$8 \cdot y^(4) — y = 0$$ $ $y \left(8 \cdot y^(3) -1\right)=0$$ В резултат се получават 2 стационарни точки:
1) $y=0 \Дясна стрелка x = 0, M_(1) = \left(0, 0\right)$;
2) $\displaystyle 8 \cdot y^(3) -1=0 \Rightarrow y^(3)=\frac(1)(8) \Rightarrow y = \frac(1)(2) \Rightarrow x=1 , M_(2) = \left(\frac(1)(2), 1\right)$
Нека проверим дали е изпълнено достатъчното условие за екстремум:
$$\displaystyle \frac(\partial^(2) f)(\partial x^(2))=6 \cdot x; \frac(\partial^(2) f)(\partial x \partial y)=-6; \frac(\partial^(2) f)(\partial y^(2))=48 \cdot y$$
1) За точката $M_(1)= \left(0,0\right)$:
$$\displaystyle A_(1)=\frac(\partial^(2) f)(\partial x^(2)) \left(0,0\right)=0; B_(1)=\frac(\partial^(2) f)(\partial x \partial y) \left(0,0\right)=-6; C_(1)=\frac(\partial^(2) f)(\partial y^(2)) \left(0,0\right)=0;$$
$A_(1) \cdot B_(1) — C_(1)^(2) = -36<0$ , значит, в точке $M_{1}$ нет экстремума.
2) За точка $M_(2)$:
$$\displaystyle A_(2)=\frac(\partial^(2) f)(\partial x^(2)) \left(1,\frac(1)(2)\right)=6; B_(2)=\frac(\partial^(2) f)(\partial x \partial y) \left(1,\frac(1)(2)\right)=-6; C_(2)=\frac(\partial^(2) f)(\partial y^(2)) \left(1,\frac(1)(2)\right)=24;$$
$A_(2) \cdot B_(2) — C_(2)^(2) = 108>0$, което означава, че в точка $M_(2)$ има екстремум и тъй като $A_(2)> 0$, тогава това е минимумът.
Отговор: Точката $\displaystyle M_(2)\left(1,\frac(1)(2)\right)$ е минималната точка на функцията $f$. - Изследвайте функцията за екстремума $f=y^(2) + 2 \cdot x \cdot y - 4 \cdot x - 2 \cdot y - 3$.
РешениеНека намерим неподвижни точки: $$\displaystyle \frac(\partial f)(\partial x)=2 \cdot y - 4;$$ $$\displaystyle \frac(\partial f)(\partial y)=2 \ cdot y + 2 \cdot x — 2.$$
Нека съставим и решим системата: $$\displaystyle \begin(cases)\frac(\partial f)(\partial x)= 0\\\frac(\partial f)(\partial y)= 0\end(cases ) \ Rightarrow \begin(cases)2 \cdot y - 4= 0\\2 \cdot y + 2 \cdot x - 2 = 0\end(cases) \Rightarrow \begin(cases) y = 2\\y + x = 1\end(cases) \Rightarrow x = -1$$
$M_(0) \left(-1, 2\right)$ е неподвижна точка.
Нека проверим дали е изпълнено достатъчното условие за екстремума: $$\displaystyle A=\frac(\partial^(2) f)(\partial x^(2)) \left(-1,2\right)=0 ; B=\frac(\partial^(2) f)(\partial x \partial y) \left(-1,2\right)=2; C=\frac(\partial^(2) f)(\partial y^(2)) \left(-1,2\right)=2;$$
$A \cdot B — C^(2) = -4<0$ , значит, в точке $M_{0}$ нет экстремума.
Отговор: няма крайности.
Времево ограничение: 0
Навигация (само номера на задания)
0 от 4 изпълнени задачи
Информация
Направете този тест, за да проверите знанията си по темата, която току-що прочетохте: Локални екстремуми на функции на множество променливи.
Вече сте правили теста преди. Не можете да го започнете отново.
Тестът се зарежда...
Трябва да влезете или да се регистрирате, за да започнете теста.
Трябва да завършите следните тестове, за да започнете този:
Резултати
Верни отговори: 0 от 4
Вашето време:
Времето изтече
Постигнахте 0 от 0 точки (0)
Вашият резултат е записан в класацията
- С отговор
- С маркировка за гледане
Задача 2 от 4
2 .
Брой точки: 1Функцията $f = 4 + \sqrt((x^(2)+y^(2))^(2))$ има ли екстремум
Задача 1 от 4
1 .
Брой точки: 1Изследвайте функцията $f$ за екстремуми: $f=e^(x+y)(x^(2)-2 \cdot y^(2))$
вярно
погрешно
Екстремалната точка на функция е точката в областта на дефиниране на функцията, в която стойността на функцията приема минимална или максимална стойност. Стойностите на функцията в тези точки се наричат екстремуми (минимум и максимум) на функцията.
Определение. Точка х1 функционална област f(х) се нарича максимална точка на функцията , ако стойността на функцията в тази точка е по-голяма от стойностите на функцията в точки, достатъчно близки до нея, разположени отдясно и отляво на нея (т.е. неравенството е в сила f(х0 ) > f(х 0 + Δ х) х1 максимум.
Определение. Точка х2 функционална област f(х) се нарича минимална точка на функцията, ако стойността на функцията в тази точка е по-малка от стойностите на функцията в точки, достатъчно близки до нея, разположени отдясно и отляво на нея (т.е. неравенството е в сила f(х0 ) < f(х 0 + Δ х) ). В този случай казваме, че функцията има в точката х2 минимум.
Да кажем точка х1 - максимална точка на функцията f(х) . След това в интервала до х1 функцията се увеличава, следователно производната на функцията е по-голяма от нула ( f "(х) > 0 ), и в интервала след х1 функцията намалява, следователно, производна на функцияпо-малко от нула ( f "(х) < 0 ). Тогда в точке х1
Нека приемем също, че точката х2 - минимална точка на функцията f(х) . След това в интервала до х2 функцията е намаляваща и производната на функцията е по-малка от нула ( f "(х) < 0 ), а в интервале после х2 функцията нараства и производната на функцията е по-голяма от нула ( f "(х) > 0 ). В този случай също в точката х2 производната на функцията е нула или не съществува.
Теорема на Ферма (необходим знак за съществуването на екстремум на функция). Ако точката х0 - екстремна точка на функцията f(х), тогава в тази точка производната на функцията е равна на нула ( f "(х) = 0 ) или не съществува.
Определение. Точките, в които производната на дадена функция е нула или не съществува, се наричат критични точки .

Пример 1.Нека разгледаме функцията.
В точката х= 0 производната на функцията е нула, следователно точката х= 0 е критичната точка. Въпреки това, както може да се види на графиката на функцията, тя нараства в цялата област на дефиниция, така че точката х= 0 не е екстремната точка на тази функция.
По този начин условията, че производната на функция в точка е равна на нула или не съществува, са необходими условия за екстремум, но не са достатъчни, тъй като могат да бъдат дадени други примери за функции, за които тези условия са изпълнени, но функцията няма екстремум в съответната точка. Ето защо трябва да има достатъчно доказателства, което позволява да се прецени дали има екстремум в дадена критична точка и какъв е екстремумът – максимален или минимален.
Теорема (първият достатъчен признак за съществуването на екстремум на функция).Критична точка х0 f(х) ако при преминаване през тази точка производната на функцията промени знака и ако знакът се промени от "плюс" на "минус", тогава това е максимална точка, а ако от "минус" на "плюс", тогава това е минимална точка.
Ако е близо до точката х0 , вляво и вдясно от нея, производната запазва знака си, това означава, че функцията или само намалява, или само нараства в определена околност на точката х0 . В този случай в точката х0 няма крайност.
така че за да определите екстремалните точки на функцията, трябва да направите следното :
- Намерете производната на функцията.
- Приравнете производната на нула и определете критичните точки.
- Мислено или на хартия маркирайте критичните точки на числовата линия и определете знаците на производната на функцията в получените интервали. Ако знакът на производната се промени от "плюс" на "минус", тогава критичната точка е максималната точка, а ако от "минус" на "плюс", тогава минималната точка.
- Изчислете стойността на функцията в точките на екстремума.

Пример 2.Намерете екстремумите на функцията ![]() .
.
Решение. Нека намерим производната на функцията:
Нека приравним производната на нула, за да намерим критичните точки:
![]() .
.
Тъй като за всякакви стойности на "x" знаменателят не е равен на нула, ние приравняваме числителя на нула:
Имам една критична точка х= 3 . Нека определим знака на производната в интервалите, ограничени от тази точка:
в диапазона от минус безкрайност до 3 - знак минус, тоест функцията намалява,
в интервала от 3 до плюс безкрайност има знак плюс, тоест функцията нараства.
Тоест точка х= 3 е минималната точка.
Нека намерим стойността на функцията в минималната точка:
Така се намира екстремната точка на функцията: (3; 0) и тя е минималната точка.
Теорема (вторият достатъчен признак за съществуването на екстремум на функция).Критична точка х0 е екстремната точка на функцията f(х), ако втората производна на функцията в тази точка не е равна на нула ( f ""(х) ≠ 0 ), и ако втората производна е по-голяма от нула ( f ""(х) > 0), тогава максималната точка и ако втората производна е по-малка от нула ( f ""(х) < 0 ), то точкой минимума.
Забележка 1. Ако в точката х0 Ако и първата, и втората производни са нулеви, тогава в този момент е невъзможно да се прецени наличието на екстремум въз основа на втория достатъчен критерий. В този случай трябва да използвате първия достатъчен критерий за екстремума на функция.
Забележка 2. Вторият достатъчен критерий за екстремум на функция не е приложим дори когато първата производна не съществува в стационарна точка (тогава втората производна също не съществува). В този случай трябва да използвате и първия достатъчен знак за екстремум на функция.
Локален характер на екстремумите на функцията
От горните определения следва, че екстремумът на функцията има локален характер - той е най-големият и най-малка стойностфункции в сравнение с близки стойности.
Да приемем, че разглеждате приходите си за период от една година. Ако през май сте спечелили 45 000 рубли, а през април 42 000 рубли и през юни 39 000 рубли, тогава приходите от май са максимумът на функцията за печалба в сравнение с близките стойности. Но през октомври сте спечелили 71 000 рубли, през септември 75 000 рубли, а през ноември 74 000 рубли, така че приходите през октомври са минимумът на функцията за печалба в сравнение с близките стойности. И можете лесно да видите, че максимумът сред стойностите на април-май-юни е по-малък от минимума на септември-октомври-ноември.
Най-общо казано, на интервал една функция може да има няколко екстремума и може да се окаже, че някакъв минимум на функцията е по-голям от всеки максимум. И така, за функцията, показана на фигурата по-горе, .
Тоест, не трябва да се мисли, че максимумът и минимумът на функцията са съответно нейните най-големи и най-малки стойности в целия разглеждан сегмент. В максималната точка функцията има най-голяма стойност само в сравнение с онези стойности, които има във всички точки, достатъчно близки до максималната точка, а в минималната точка има най-малка стойност само в сравнение с тези стойности че има във всички точки достатъчно близо до минималната точка.
Следователно можем да изясним горната концепция за екстремни точки на функция и да наречем минималните точки локални минимални точки, а максималните точки локални максимални точки.
Търсим заедно екстремума на функцията

Пример 3.
Решение: Функцията е дефинирана и непрекъсната на цялата числова ос. Негова производна ![]() също съществува на цялата числова ос. Следователно в случая критичните точки са само тези, при които, т.е. , от къде и . Критични точки и разделя цялата област на дефиниране на функцията на три интервала на монотонност: . Нека изберем по една контролна точка във всяка от тях и да намерим знака на производната в тази точка.
също съществува на цялата числова ос. Следователно в случая критичните точки са само тези, при които, т.е. , от къде и . Критични точки и разделя цялата област на дефиниране на функцията на три интервала на монотонност: . Нека изберем по една контролна точка във всяка от тях и да намерим знака на производната в тази точка.
За интервала контролната точка може да бъде: намери. Като вземем точка от интервала, получаваме, и вземем точка от интервала, имаме. И така, в интервалите и , и в интервала . Според първия достатъчен критерий за екстремум в точката няма екстремум (тъй като производната запазва знака си в интервала), а в точката функцията има минимум (тъй като производната променя знака от минус на плюс при преминаване през тази точка). Нека намерим съответните стойности на функцията: , a . В интервала функцията намалява, тъй като в този интервал , а в интервала нараства, тъй като в този интервал .
За да изясним конструкцията на графиката, намираме нейните точки на пресичане с координатните оси. Когато получим уравнение, чиито корени са и , т.е. две точки (0; 0) и (4; 0) от графиката на функцията са намерени. Използвайки цялата получена информация, изграждаме графика (вижте началото на примера).

Пример 4.Намерете екстремума на функцията и изградете нейната графика.
Областта на дефиниране на функция е цялата числова ос, с изключение на точката, т.е. .
За да съкратите изследването, можете да използвате факта, че тази функция е четна, тъй като  . Следователно неговата графика е симетрична спрямо оста Ойи изследването може да се извърши само за интервала.
. Следователно неговата графика е симетрична спрямо оста Ойи изследването може да се извърши само за интервала.
Намиране на производната ![]() и критични точки на функцията:
и критични точки на функцията:
1) 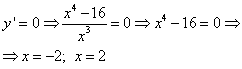 ;
;
2) ![]() ,
,
но функцията претърпява прекъсване в тази точка, така че не може да бъде точка на екстремум.
Така дадената функция има две критични точки: и . Като вземем предвид четността на функцията, ще проверим само точката, използвайки втория достатъчен критерий за екстремум. За да направим това, намираме втората производна ![]() и определете неговия знак при: получаваме . Тъй като и , това е минималната точка на функцията и
и определете неговия знак при: получаваме . Тъй като и , това е минималната точка на функцията и ![]() .
.
За да получите по-пълна картина на графиката на функция, нека разберем нейното поведение в границите на домейна на дефиниция:

(тук символът показва желанието хдо нула от дясно, и хостава положителен; по подобен начин означава стремеж хдо нула отляво и хостава отрицателна). По този начин, ако , тогава . След това намираме
 ,
,
тези. ако , тогава .
Графиката на функцията няма пресечни точки с осите. Картината е в началото на примера.
Продължаваме заедно да търсим екстремуми на функцията
Пример 8.Намерете екстремумите на функцията.

Решение. Нека намерим областта на дефиниция на функцията. Тъй като неравенството трябва да бъде изпълнено, получаваме от .
Нека намерим първата производна на функцията:

Нека намерим критичните точки на функцията.
$E \подмножество \mathbb(R)^(n)$. Казват, че $f$ има локален максимумв точката $x_(0) \in E$, ако има околност $U$ на точката $x_(0)$ такава, че за всички $x \in U$ неравенството $f\left(x\right ) \leqslant f е изпълнено \left(x_(0)\right)$.
Локалният максимум се нарича строг , ако околността $U$ може да бъде избрана така, че за всички $x \in U$, различни от $x_(0)$, да има $f\left(x\right)< f\left(x_{0}\right)$.
Определение
Нека $f$ е реална функция в отвореното множество $E \subset \mathbb(R)^(n)$. Казват, че $f$ има местен минимумв точката $x_(0) \in E$, ако има околност $U$ на точката $x_(0)$ такава, че за всички $x \in U$ неравенството $f\left(x\right ) \geqslant f \left(x_(0)\right)$.
Локален минимум се нарича строг, ако квартал $U$ може да бъде избран така, че за всички $x \in U$, различни от $x_(0)$, да има $f\left(x\right) > f\left(x_ ( 0)\вдясно)$.
Локалният екстремум съчетава понятията локален минимум и локален максимум.
Теорема (необходимо условие за екстремума на диференцируема функция)
Нека $f$ е реална функция в отвореното множество $E \subset \mathbb(R)^(n)$. Ако в точката $x_(0) \in E$ функцията $f$ има локален екстремум в тази точка, тогава $$\text(d)f\left(x_(0)\right)=0.$$ Равен на нула диференциал е еквивалентен на факта, че всички са равни на нула, т.е. $$\displaystyle\frac(\partial f)(\partial x_(i))\left(x_(0)\right)=0.$$
В едномерния случай това е – . Нека обозначим $\phi \left(t\right) = f \left(x_(0)+th\right)$, където $h$ е произволен вектор. Функцията $\phi$ е дефинирана за стойности на $t$, които са достатъчно малки по абсолютна стойност. В допълнение, той е диференцируем по отношение на и $(\phi)’ \left(t\right) = \text(d)f \left(x_(0)+th\right)h$.
Нека $f$ има локален максимум в точка x $0$. Това означава, че функцията $\phi$ при $t = 0$ има локален максимум и според теоремата на Ферма $(\phi)' \left(0\right)=0$.
И така, получихме, че $df \left(x_(0)\right) = 0$, т.е. функция $f$ в точка $x_(0)$ е равна на нула върху всеки вектор $h$.
Определение
Точки, в които диференциалът е нула, т.е. тези, при които всички частни производни са равни на нула, се наричат стационарни. Критични точкифункции $f$ са тези точки, в които $f$ не е диференцируемо или е равно на нула. Ако точката е неподвижна, тогава от това не следва, че функцията има екстремум в тази точка.
Пример 1.
Нека $f \left(x,y\right)=x^(3)+y^(3)$. Тогава $\displaystyle\frac(\partial f)(\partial x) = 3 \cdot x^(2)$,$\displaystyle\frac(\partial f)(\partial y) = 3 \cdot y^(2 )$, така че $\left(0,0\right)$ е стационарна точка, но функцията няма екстремум в тази точка. Наистина, $f \left(0,0\right) = 0$, но е лесно да се види, че във всяка околност на точката $\left(0,0\right)$ функцията приема както положителни, така и отрицателни стойности.
Пример 2.
Функцията $f \left(x,y\right) = x^(2) − y^(2)$ има стационарна точка в началото си, но е ясно, че в тази точка няма екстремум.
Теорема (достатъчно условие за екстремум).
Нека функцията $f$ е два пъти непрекъснато диференцируема върху отвореното множество $E \subset \mathbb(R)^(n)$. Нека $x_(0) \in E$ е неподвижна точка и $$\displaystyle Q_(x_(0)) \left(h\right) \equiv \sum_(i=1)^n \sum_(j=1 ) ^n \frac(\partial^(2) f)(\partial x_(i) \partial x_(j)) \left(x_(0)\right)h^(i)h^(j).$ $ Тогава
- ако $Q_(x_(0))$ – , тогава функцията $f$ в точката $x_(0)$ има локален екстремум, а именно минимум, ако формата е положително определена, и максимум, ако формата е отрицателно определено;
- ако квадратичната форма $Q_(x_(0))$ е недефинирана, тогава функцията $f$ в точката $x_(0)$ няма екстремум.
Нека използваме разширението по формулата на Тейлър (12.7 стр. 292). Като се има предвид, че частичните производни от първи ред в точката $x_(0)$ са равни на нула, получаваме $$\displaystyle f \left(x_(0)+h\right)−f \left(x_(0)\ дясно) = \ frac(1)(2) \sum_(i=1)^n \sum_(j=1)^n \frac(\partial^(2) f)(\partial x_(i) \partial x_ (j)) \left(x_(0)+\theta h\right)h^(i)h^(j),$$ където $0<\theta<1$. Обозначим $\displaystyle a_{ij}=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right)$. В силу теоремы Шварца (12.6 стр. 289-290) , $a_{ij}=a_{ji}$. Обозначим $$\displaystyle \alpha_{ij} \left(h\right)=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}+\theta h\right)−\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right).$$ По предположению, все непрерывны и поэтому $$\lim_{h \rightarrow 0} \alpha_{ij} \left(h\right)=0. \left(1\right)$$ Получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left.$$ Обозначим $$\displaystyle \epsilon \left(h\right)=\frac{1}{|h|^{2}}\sum_{i=1}^n \sum_{j=1}^n \alpha_{ij} \left(h\right)h_{i}h_{j}.$$ Тогда $$|\epsilon \left(h\right)| \leq \sum_{i=1}^n \sum_{j=1}^n |\alpha_{ij} \left(h\right)|$$ и, в силу соотношения $\left(1\right)$, имеем $\epsilon \left(h\right) \rightarrow 0$ при $h \rightarrow 0$. Окончательно получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left. \left(2\right)$$ Предположим, что $Q_{x_{0}}$ – положительноопределенная форма. Согласно лемме о положительноопределённой квадратичной форме (12.8.1 стр. 295, Лемма 1) , существует такое положительное число $\lambda$, что $Q_{x_{0}} \left(h\right) \geqslant \lambda|h|^{2}$ при любом $h$. Поэтому $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right) \geq \frac{1}{2}|h|^{2} \left(λ+\epsilon \left(h\right)\right).$$ Так как $\lambda>0$ и $\epsilon \left(h\right) \rightarrow 0$ за $h \rightarrow 0$, тогава дясната страна ще бъде положителна за всеки вектор $h$ с достатъчно малка дължина.
И така, стигнахме до заключението, че в някаква околност на точката $x_(0)$ неравенството $f \left(x\right) >f \left(x_(0)\right)$ е в сила, ако само $ x \neq x_ (0)$ (поставяме $x=x_(0)+h$\right). Това означава, че в точката $x_(0)$ функцията има строг локален минимум и по този начин първата част от нашата теорема е доказана.
Нека сега приемем, че $Q_(x_(0))$ е неопределена форма. Тогава има вектори $h_(1)$, $h_(2)$, така че $Q_(x_(0)) \left(h_(1)\right)=\lambda_(1)>0$, $Q_ ( x_(0)) \left(h_(2)\right)= \lambda_(2)<0$. В соотношении $\left(2\right)$ $h=th_{1}$ $t>$0. Тогава получаваме $$f \left(x_(0)+th_(1)\right)−f \left(x_(0)\right) = \frac(1)(2) \left[ t^(2) \ lambda_(1) + t^(2) |h_(1)|^(2) \epsilon \left(th_(1)\right) \right] = \frac(1)(2) t^(2) \ left[ \lambda_(1) + |h_(1)|^(2) \epsilon \left(th_(1)\right) \right].$$ За достатъчно малък $t>0$, дясната страна е положителна. Това означава, че във всяка близост на точката $x_(0)$ функцията $f$ приема стойности $f \left(x\right)$, по-големи от $f \left(x_(0)\right)$.
По същия начин откриваме, че във всяка околност на точката $x_(0)$ функцията $f$ приема стойности, по-малки от $f \left(x_(0)\right)$. Това заедно с предходното означава, че в точката $x_(0)$ функцията $f$ няма екстремум.
Нека разгледаме специален случай на тази теорема за функцията $f \left(x,y\right)$ на две променливи, дефинирани в някаква околност на точката $\left(x_(0),y_(0)\right )$ и имащи непрекъснати частни производни от първи и втори ред. Да приемем, че $\left(x_(0),y_(0)\right)$ е стационарна точка и обозначаваме $$\displaystyle a_(11)= \frac(\partial^(2) f)(\partial x ^ (2)) \left(x_(0) ,y_(0)\right), a_(12)=\frac(\partial^(2) f)(\partial x \partial y) \left(x_( 0) ), y_(0)\right), a_(22)=\frac(\partial^(2) f)(\partial y^(2)) \left(x_(0), y_(0)\right ) .$$ Тогава предишната теорема приема следната форма.
Теорема
Нека $\Delta=a_(11) \cdot a_(22) − a_(12)^2$. След това:
- ако $\Delta>0$, тогава функцията $f$ има локален екстремум в точката $\left(x_(0),y_(0)\right)$, а именно минимум, ако $a_(11)> 0$ и максимум, ако $a_(11)<0$;
- ако $\Delta<0$, то экстремума в точке $\left(x_{0},y_{0}\right)$ нет. Как и в одномерном случае, при $\Delta=0$ экстремум может быть, а может и не быть.
Примери за решаване на проблеми
Алгоритъм за намиране на екстремума на функция на много променливи:
- Намиране на стационарни точки;
- Намерете диференциала от 2-ри ред във всички неподвижни точки
- Използвайки достатъчното условие за екстремума на функция от много променливи, ние разглеждаме диференциала от 2-ри ред във всяка стационарна точка
- Изследвайте функцията за екстремум $f \left(x,y\right) = x^(3) + 8 \cdot y^(3) + 18 \cdot x — 30 \cdot y$.
РешениеНека намерим частичните производни от 1-ви ред: $$\displaystyle \frac(\partial f)(\partial x)=3 \cdot x^(2) - 6 \cdot y;$$ $$\displaystyle \frac(\partial f)(\partial y)=24 \cdot y^(2) - 6 \cdot x.$$ Нека съставим и решим системата: $$\displaystyle \begin(cases)\frac(\partial f)(\partial x) = 0\\\frac(\partial f)(\partial y)= 0\end(cases) \Rightarrow \begin(cases)3 \cdot x^(2) - 6 \cdot y= 0\\24 \cdot y^(2) — 6 \cdot x = 0\end(cases) \Rightarrow \begin(cases)x^(2) — 2 \cdot y= 0\\4 \cdot y^(2) — x = 0 \end(cases)$$ От второто уравнение изразяваме $x=4 \cdot y^(2)$ - заместваме го в първото уравнение: $$\displaystyle \left(4 \cdot y^(2) \right )^(2)-2 \cdot y=0$$ $$16 \cdot y^(4) — 2 \cdot y = 0$$ $$8 \cdot y^(4) — y = 0$$ $ $y \left(8 \cdot y^(3) -1\right)=0$$ В резултат се получават 2 стационарни точки:
1) $y=0 \Дясна стрелка x = 0, M_(1) = \left(0, 0\right)$;
2) $\displaystyle 8 \cdot y^(3) -1=0 \Rightarrow y^(3)=\frac(1)(8) \Rightarrow y = \frac(1)(2) \Rightarrow x=1 , M_(2) = \left(\frac(1)(2), 1\right)$
Нека проверим дали е изпълнено достатъчното условие за екстремум:
$$\displaystyle \frac(\partial^(2) f)(\partial x^(2))=6 \cdot x; \frac(\partial^(2) f)(\partial x \partial y)=-6; \frac(\partial^(2) f)(\partial y^(2))=48 \cdot y$$
1) За точката $M_(1)= \left(0,0\right)$:
$$\displaystyle A_(1)=\frac(\partial^(2) f)(\partial x^(2)) \left(0,0\right)=0; B_(1)=\frac(\partial^(2) f)(\partial x \partial y) \left(0,0\right)=-6; C_(1)=\frac(\partial^(2) f)(\partial y^(2)) \left(0,0\right)=0;$$
$A_(1) \cdot B_(1) — C_(1)^(2) = -36<0$ , значит, в точке $M_{1}$ нет экстремума.
2) За точка $M_(2)$:
$$\displaystyle A_(2)=\frac(\partial^(2) f)(\partial x^(2)) \left(1,\frac(1)(2)\right)=6; B_(2)=\frac(\partial^(2) f)(\partial x \partial y) \left(1,\frac(1)(2)\right)=-6; C_(2)=\frac(\partial^(2) f)(\partial y^(2)) \left(1,\frac(1)(2)\right)=24;$$
$A_(2) \cdot B_(2) — C_(2)^(2) = 108>0$, което означава, че в точка $M_(2)$ има екстремум и тъй като $A_(2)> 0$, тогава това е минимумът.
Отговор: Точката $\displaystyle M_(2)\left(1,\frac(1)(2)\right)$ е минималната точка на функцията $f$. - Изследвайте функцията за екстремума $f=y^(2) + 2 \cdot x \cdot y - 4 \cdot x - 2 \cdot y - 3$.
РешениеНека намерим неподвижни точки: $$\displaystyle \frac(\partial f)(\partial x)=2 \cdot y - 4;$$ $$\displaystyle \frac(\partial f)(\partial y)=2 \ cdot y + 2 \cdot x — 2.$$
Нека съставим и решим системата: $$\displaystyle \begin(cases)\frac(\partial f)(\partial x)= 0\\\frac(\partial f)(\partial y)= 0\end(cases ) \ Rightarrow \begin(cases)2 \cdot y - 4= 0\\2 \cdot y + 2 \cdot x - 2 = 0\end(cases) \Rightarrow \begin(cases) y = 2\\y + x = 1\end(cases) \Rightarrow x = -1$$
$M_(0) \left(-1, 2\right)$ е неподвижна точка.
Нека проверим дали е изпълнено достатъчното условие за екстремума: $$\displaystyle A=\frac(\partial^(2) f)(\partial x^(2)) \left(-1,2\right)=0 ; B=\frac(\partial^(2) f)(\partial x \partial y) \left(-1,2\right)=2; C=\frac(\partial^(2) f)(\partial y^(2)) \left(-1,2\right)=2;$$
$A \cdot B — C^(2) = -4<0$ , значит, в точке $M_{0}$ нет экстремума.
Отговор: няма крайности.
Времево ограничение: 0
Навигация (само номера на задания)
0 от 4 изпълнени задачи
Информация
Направете този тест, за да проверите знанията си по темата, която току-що прочетохте: Локални екстремуми на функции на множество променливи.
Вече сте правили теста преди. Не можете да го започнете отново.
Тестът се зарежда...
Трябва да влезете или да се регистрирате, за да започнете теста.
Трябва да завършите следните тестове, за да започнете този:
Резултати
Верни отговори: 0 от 4
Вашето време:
Времето изтече
Постигнахте 0 от 0 точки (0)
Вашият резултат е записан в класацията
- С отговор
- С маркировка за гледане
Задача 2 от 4
2 .
Брой точки: 1Функцията $f = 4 + \sqrt((x^(2)+y^(2))^(2))$ има ли екстремум
Задача 1 от 4
1 .
Брой точки: 1Изследвайте функцията $f$ за екстремуми: $f=e^(x+y)(x^(2)-2 \cdot y^(2))$
вярно
погрешно
определение:Точка x0 се нарича точка на локален максимум (или минимум) на функция, ако в някаква близост на точка x0 функцията приема най-голямата (или най-малката) стойност, т.е. за всички x от някаква околност на точката x0 условието f(x) f(x0) (или f(x) f(x0)) е изпълнено.
Точките на локален максимум или минимум са обединени от общо наименование - точки на локален екстремум на функция.
Обърнете внимание, че в локални точки на екстремум функцията достига своята максимална или минимална стойност само в определен локален регион. Възможни са случаи, когато според стойността уmaxуmin.
Необходим признак за съществуването на локален екстремум на функция
Теорема . Ако непрекъсната функция y = f(x) има локален екстремум в точката x0, тогава в тази точка първата производна е или нула, или не съществува, т.е. възниква локален екстремум в критични точки от първи вид.
В локалните точки на екстремум или допирателната е успоредна на оста 0x, или има две допирателни (вижте фигурата). Имайте предвид, че критичните точки са необходимо, но не достатъчно условие за локален екстремум. Локален екстремум възниква само в критични точки от първи вид, но не във всички критични точки възниква локален екстремум.
Например: кубична парабола y = x3 има критична точка x0 = 0, в която производната y/(0)=0, но критичната точка x0=0 не е екстремна точка, а инфлексна точка при нея (вижте по-долу).
Достатъчен признак за съществуването на локален екстремум на функция
Теорема . Ако, когато аргументът преминава през критична точка от първи вид отляво надясно, първата производна y / (x)
променя знака от “+” на “-”, тогава непрекъснатата функция y(x) в тази критична точка има локален максимум;
променя знака от „-“ на „+“, тогава непрекъснатата функция y(x) има локален минимум в тази критична точка
не променя знака, тогава в тази критична точка няма локален екстремум, тук има инфлексна точка.
За локален максимум областта на нарастваща функция (y/0) се заменя с област на намаляваща функция (y/0). За локален минимум областта на намаляваща функция (y/0) се заменя с област на нарастваща функция (y/0).
Пример: Изследвайте функцията y = x3 + 9x2 + 15x - 9 за монотонност, екстремум и постройте графика на функцията.
Нека намерим критични точки от първи вид, като дефинираме производната (y/) и я приравним към нула: y/ = 3x2 + 18x + 15 =3(x2 + 6x + 5) = 0
Нека решим квадратния трином с помощта на дискриминанта:
x2 + 6x + 5 = 0 (a=1, b=6, c=5) D= , x1k = -5, x2k = -1.
2) Разделяме числовата ос на 3 области с критични точки и определяме знаците на производната (y/) в тях. С помощта на тези знаци ще намерим области на монотонност (нарастване и намаляване) на функциите, а чрез смяна на знаците ще определим точките на локален екстремум (максимум и минимум).
Представяме резултатите от изследването под формата на таблица, от която могат да се направят следните изводи:
- 1. В интервала y /(-10) 0 функцията нараства монотонно (знакът на производната y беше оценен с помощта на контролната точка x = -10, взета в този интервал);
- 2. В интервала (-5 ; -1) y /(-2) 0 функцията намалява монотонно (знакът на производната y се оценява с помощта на контролната точка x = -2, взета в този интервал);
- 3. В интервала y /(0) 0 функцията нараства монотонно (знакът на производната y се оценява с помощта на контролната точка x = 0, взета в този интервал);
- 4. При преминаване през критичната точка x1k = -5, производната променя знака от “+” на “-”, следователно тази точка е локална максимална точка
- (ymax(-5) = (-5)3+9(-5)2 +15(-5)-9=-125 + 225 - 75 - 9 =16);
- 5. При преминаване през критичната точка x2k = -1, производната променя знака от “-” на “+”, следователно тази точка е локална минимална точка
- (ymin(-1) = -1 + 9 - 15 - 9 = - 16).
x -5 (-5; -1) -1
3) Ще изградим графика въз основа на резултатите от изследването, като използваме допълнителни изчисления на стойностите на функцията в контролни точки:
конструира правоъгълна координатна система Oxy;
Показваме чрез координати точките на максимум (-5; 16) и минимум (-1;-16);
за да изясним графиката, изчисляваме стойността на функцията в контролни точки, като ги избираме отляво и отдясно на максималните и минималните точки и вътре в средния интервал, например: y(-6)=(-6)3 + 9(-6)2+15(-6 )-9=9; y(-3)=(-3)3+9(-3)2+15(-3)-9=0;
y(0)= -9 (-6;9); (-3;0) и (0;-9) - изчислени контролни точки, които нанасяме за построяване на графиката;
Показваме графиката под формата на крива, изпъкнала нагоре в максималната точка и изпъкнала надолу в минималната точка и минаваща през изчислените контролни точки.