Actions on vectors Examples. Vectors and surgery over vectors. Vector connection with a rectangular Cartesian coordinate system in space

VECTOR
In physics and mathematics, the vector is a value that is characterized by its numerical value and direction. A lot of important values \u200b\u200bthat are vectors are found in physics, such as force, position, speed, acceleration, torque, impulse, electric and magnetic fields. They can be opposed to other values, such as mass, volume, pressure, temperature and density that can be described in a conventional number, and they are called "scalars". The vectorial is used when working with values \u200b\u200bthat cannot be set completely using conventional numbers. For example, we want to describe the position of the subject relative to some point. We can say how many kilometers from point to the subject, but we cannot completely determine its location until we know the direction in which it is. Thus, the location of the subject is characterized by a numerical value (distance in kilometers) and the direction. Graphically, the vectors are depicted in the form of directed segments of a direct length, as in Fig. 1. For example, in order to present graphically strength of five kilograms, it is necessary to draw a stretch of a straight line in five units in the direction of force. The arrow indicates that the force acts from A to B; If the force acts from B to A, we would record or for convenience, the vectors are usually designated by bold uppercase letters (a, b, c and so on); Vectors A and -a have equal numerical values, but are opposite to the direction. The numerical value of the vector A is called the module or length and is denoted by A or | A |. This is a magnitude, of course, scalar. The vector, the beginning and the end of which coincide, is called zero and designated O.

Two vectors are called equal (or free) if their modules and directions coincide. In mechanics and physics, this definition, however, should be used with caution, since two equal forces attached to different points of the body will generally lead to various results. In this regard, the vectors are divided into "related" or "sliding", as follows: The associated vectors have fixed points of the application. For example, a radius-vector indicates the position of the point relative to some fixed origin. Related vectors are considered equal if they coincide not only modules and directions, but they have a common point of application. Sliding vectors are called equal vectors located on one straight line.
Addition of vectors. The idea of \u200b\u200badding vectors arose from the fact that we can find the only vector that has the same impact as the other two vector together. If in order to get into some point, we need to go first a kilometers in one direction and then b kilometers in another direction, then we could achieve our end point by passing with kilometers in the third direction (Fig. 2). In this sense, we can say that

A + B \u003d C.
The vector C is called the "resulting vector" A and B, it is set by the construction shown in the figure; In vectors A and B, as parties are constructed by parallelograms, and C is a diagonal that connects the beginning A and the end of V. from fig. 2 It can be seen that the addition of vectors "commutative", i.e. A + b \u003d b + a. Similarly, you can add up several vectors that convene them by the "continuous chain", as shown in Fig. 3 for three vectors D, E and F. From fig. 3 is also seen that

(D + E) + F \u003d D + (E + F), i.e. Addition of vectors associative. You can sum up any number of vectors, and the vectors do not necessarily lie in the same plane. The subtraction of the vectors seems to be addressed with a negative vector. For example, a - b \u003d a + (-b), where, as defined earlier, -b is a vector equal to module, but opposite in direction. This formation rule can now be used as a real verification criterion, whether some value is a vector or not. Movements are usually subject to the conditions of this rule; The same can be said about speeds; Forces add up in the same way as it was possible to see from the "triangle of forces". However, some values \u200b\u200bpossessing both numerical values \u200b\u200band directions are not subject to this rule, therefore cannot be considered as vectors. Examples are finite rotations.
Multiplying vector on scalar. The product Ma or Am, where M (m No. 0) is a scalar, and a - a nonzero vector is defined as another vector, which in m times longer than A and has the direction that and a, if the number M is positive, and the opposite, if M Negative, as shown in Fig. 4, where m is 2 and -1/2, respectively. In addition, 1a \u003d a, i.e. When multiplying, 1 vector does not change. The value is -1a - the vector equal to the length, but the opposite direction, is usually written as -a. If a is zero vector and (or) m \u003d 0, then Ma is a zero vector. Multiplication Distribution, i.e.

We can add any number of vectors, and the procedure of the components does not affect the result. Right and reverse: any vector is folded into two or more "components", i.e. For two vectors or more, which, being folded, will give the source vector as the result. For example, in Fig. 2, a and b - Components C. Many mathematical actions are simplified with vectors, if the vector of three components decompose on three mutually perpendicular directions. Choose the right system of Cartesian coordinates with Ox, OY and OZ axes as shown in Fig. 5. Under the right coordinate system, we mean that the X, Y and Z axes are located as they can be located respectively large, index and middle fingers of the right hand. From one right coordinate system, you can always obtain another right coordinate system with the corresponding rotation. In fig. 5, the decomposition of the vector A is shown to three components and they are in the amount of vector A, since

Hence,

It would also be possible to first add and get then to add projections of the vector A into three coordinate axes, indicated by AX, AY and AZ are called "scalar components" of the vector A:

where A, B and G are angles between A and three coordinate axes. Now we introduce three vector of single length i, j and k (orts), having the same direction as the corresponding axes x, y and z. Then, if AX is multiplied by i, then the resulting product is a vector equal to and

Two vectors are equal then and only if their respective scalar components are equal. Thus, a \u003d b is then and only if AX \u003d BX, AY \u003d BY, AZ \u003d BZ. Two vectors can be folded by folding their components:

In addition, according to Pythagore's theorem:

Linear functions. Expression AA + BB, where a and b - scalar is called the linear function of vectors A and B. This is a vector in the same plane as A and B; If a and b are not parallel, then with a change in A and B, the AA + BB vector will move across the entire plane (Fig. 6). If A, B and C are not all lie in the same plane, then the vector AA + BB + CC (A, B and C changes) moves throughout the space. Suppose that A, B and C are single vectors I, J and K. Vector AI lies on the x axis; Vector AI + BJ can move throughout the XY plane; Vector AI + BJ + CK can be moved throughout the space.

It would be possible to choose four mutually perpendicular vector i, j, k and l and determine the four-dimensional vector as the value A \u003d AXI + AYJ + AZK + AWL
With long

And it would be possible to continue to five, six or any number of measurements. Although it is impossible to present visually such a vector, no mathematical difficulties arise here. Such a record is often useful; For example, the condition of the moving particle is described by the six-dimensional P (x, y, z, px, py, px, x, z, px, py, pz), the components of which is its position in the space (x, y, z) and the impulse (PX, PY, PZ). Such space is called "phase space"; If we consider two particles, then the phase space is 12-dimensional, if three, then 18 and so on. The number of dimensions can be increased indefinitely; At the same time, the magnitles with whom we will deal, behave in many ways as well as those that we consider in the remainder of this article, namely, three-dimensional vectors.
Multiplying two vectors. The rule of formation of vectors was obtained by studying the behavior of the values \u200b\u200brepresented by vectors. There are no visible reasons why two vectors could not multiply, but this multiplication will make sense only if it can be shown to its mathematical consistency; In addition, it is desirable that the work has a certain physical meaning. There are two methods of multiplication of vectors that correspond to these conditions. The result of one of them is a scalar, such a product is called a "scalar product" or "internal work" of two vectors and Achb or (A, B) is written. The result of another multiplication is a vector called "vector product" or "external work" and a * b or [] is recorded. Scalar works have a physical meaning for one-, two or three dimensions, while the vector works are defined only for three dimensions.
Scalar works. If under the action of some force F, the point to which it is applied is moved to the distance R, then the work performed is equal to the product R and components F in the R direction. This component is equal to F COS BF, RC, where BF, RC is an angle between F and R, i.e. Workd work \u003d FR COS BF, RC. This is an example of a physical substantiation of a scalar product defined for any two vectors A, B by formula
A * B \u003d AB COS BA, BS.
Since all the values \u200b\u200bof the right part of the equation are scalar, then A * B \u003d B * A; Therefore, the scalar multiplication of commutative. Scalar multiplication also has a distribution property: A * (B + C) \u003d A * B + A * s. If vectors a and b are perpendicular, then COS BA, BC is zero, and, therefore, a * b \u003d 0, even if neither a n n n zero. That is why we can not divide the vector. Suppose that we have divided both parts of the equation A * B \u003d A * C to A. This would give B \u003d C, and if division could be performed, then this equality would be the only possible result. However, if we rewrite the equation A * B \u003d A * C in the form A * (B - C) \u003d 0 and recall that (B - C) - the vector, it is clear that (B - c) is not necessarily zero and, Therefore, b should not be equal to C. These contradictory results show that the vector division is impossible. The scalar product gives another way to write the numerical value (module) of the vector: a * a \u003d aa * cos 0 ° \u003d A2;
so

Scalar product can be recorded in another way. To do this, let's remember that: a \u003d ax i + ayj + azk. notice, that

Then,

Since the latter equation contains x, y and z as the lower indices, the equation seemingly dependent on the selected specific coordinate system. However, this is not so that it is seen from the definition that does not depend on the selected coordinate axes.
Vector art. A vector or external product of vectors is called a vector, the module of which is equal to the product of their modules on the sine angle, perpendicular to the original vectors and the right three component together with them. This product is easiest to introduce, considering the ratio between speed and angular speed. First - vector; We will now show that the latter can also be interpreted as a vector. The angular velocity of the rotating body is defined as follows: Select any point on the body and carry out a perpendicular from this point to the axis of rotation. Then the angular velocity of the body is the number of radians, which this line turned per unit of time. If the angular speed is the vector, it must have a numerical value and direction. The numerical value is expressed in radians per second, the direction can be chosen along the axis of rotation, you can determine it by sending the vector in the direction in which the right-sided screw was moving when rotating along with the body. Consider the rotation of the body around the fixed axis. If you install this axis inside the ring, which in turn is fixed on the axis inserted inside the other ring, we can give a rotation of the body inside the first ring with an angular velocity W1 and then force the inner ring (and the body) to rotate with the angular velocity W2. Figure 7 explains the essence of the case; Circular arrows show directions of rotation. This body is a solid sphere with the center of O and Radius R.

Fig. 7. The sphere with the center O, rotates with an angular velocity W1 inside the BC ring, which, in turn, rotates inside the DE ring with an angular velocity W2. The sphere rotates with an angular speed equal to the amount of angular velocities and all points on direct pop "are in the instant rest.

Let us give this body a movement that is the sum of two different angular velocities. This movement is quite difficult to imagine, but it is quite obvious that the body no longer rotates a relatively fixed axis. However, it can still be said that it rotates. To show it, choose some point P on the body surface, which in the moment of time we consider in a large circle connecting the points in which two axes crosses the surface of the sphere. Lower perpendicular from P on the axis. These perpendiculars will become radii PJ and PK circles PQRS and PTUW, respectively. We will spend direct POPў passing through the center of the sphere. Now the point P, in the considered point in time, simultaneously moves around the circles, which are coming at the point P. For a small time interval DT, P moves to the distance

This distance is zero if

In this case, the point P is in a state of instant rest, and just all the points on a straight POP ". The rest of the sphere will be in motion (circles for which other points move do not concern, but intersect). Popў is thus instant The axis of rotation of the sphere, just as the wheel, rolling along the road at every moment of time, rotates relative to its lower point. What is the corner speed of the sphere? Select the point A for simplicity, in which the W1 axis crosses the surface. At the time of time we consider , it moves during DT time per distance

In the circle of radius R SIN W1. By definition, angular speed

From this formula and relation (1) we get

In other words, if you write a numerical value and choose the direction of the angular velocity as described above, then these values \u200b\u200bare folded as vectors and can be considered as such. Now you can enter a vector product; Consider the body rotating at the angular velocity w. Choose any point P on the body and any beginning of the coordinates of the oh, which is on the axis of rotation. Let R be a vector directed from O to P. Point P moves around the circle at a speed V \u003d W R sin (W, R). The velocity V vector is tangent to the circumference and indicates in the direction shown in Fig. eight.

This equation gives the dependence of the velocity V point from the combination of two vectors W and R. We use this ratio to determine a new type of product, and write: V \u003d W * R. Since the result of such multiplication is the vector, this product is called vector. For any two vectors A and B, if A * B \u003d C, then C \u003d AB SIN BA, BS, and the direction of the vector c is that it is perpendicular to the plane passing through a and b and indicates in the direction that coincides with the direction of movement of the repristent The screw, if it is parallel to C and rotates from A to B. In other words, we can say that A, B and C, located in this order, form the right set of coordinate axes. Anti-commutative vector product; Vector b * a has the same module as A * B, but is directed in the opposite direction: a * b \u003d -b * A. This product is distributive, but not associative; You can prove that

Let's see how the vector product is written in terms of components and single vectors. First of all, for any vector a, a * a \u003d aa sin 0 \u003d 0.
Consequently, in the case of single vectors, I * i \u003d j * j \u003d k * k \u003d 0 and I * j \u003d k, j * k \u003d i, k * i \u003d j. Then,

This equality can also be written as a determinant:

If A * b \u003d 0, then either a or b is equal to 0 or a and b collinear. Thus, as in the case of a scalar product, the division on the vector is impossible. The value A * B is equal to the area of \u200b\u200bthe parallelogram with the sides of A and B. It is easy to see, since B SIN BA, BS - its height and a - base. There are many other physical quantities that are vector works. One of the most important vector works appears in the theory of electromagnetism and is called the Pinging vector P. This vector is given as follows: P \u003d E * H, where E and H are the vectors of electrical and magnetic fields, respectively. Vector P can be considered as a given energy flow in watts per square meter anywhere. Here are some more examples: the moment of force F (torque) relative to the start of the coordinates acting on the point, the radius-vector of which R is defined as R * F; The particle located at R, weighing M and the speed V, has an angular moment Mr * v relative to the start of coordinates; The force acting on a particle carrying electrical charge q through a magnetic field B at a speed V, there is a QV * B.
Triple works. Of the three vectors, we can form the following triple works: vector (A * B) * C; Vector (A * B) * C; Scalar (A * B) * c. The first type is the product of C and Scalar A * B; We have already spoken about such works. The second type is called double vector product; vector A * B is perpendicular to the plane where A and B lie, and therefore (A * B) * C - the vector lying in the plane A and B and perpendicular C. Consequently, in general, (A * B) * C is not Equally A * (B * C). Recovering a, b and c through their coordinates (components) along the X, Y and Z axes and multiplying, it can be shown that A * (B * C) \u003d B * (A * C) - C * (A * B). The third type of product that occurs when calculating the lattice in solid physics is numerically equal to the volume of parallelepiped with ribs A, B, C. Since (A * B) * C \u003d A * (B * C), Signs of scalar and vector variations can be Change places, and the work is often written as (ABC). This product is equal to the determinant

Note that (a b c) \u003d 0, if all three vectors lie in the same plane or, if a \u003d 0 or (and) B \u003d 0 or (and) c \u003d 0.
Differentiation of vector
Suppose that vector U is a function of one scalar variable T. For example, U can be a radius-vector conducted from the start of coordinates to a moving point, and T - time. Let T be changed to a small amount of DT, which will lead to a change of U by the value of DU. This is shown in Fig. 9. The DU / DT ratio is a vector directed in the same direction as DU. We can define a derivative U by t as

Provided that this limit exists. On the other hand, you can submit u as the amount of the component for three axes and record

If u is a radius-vector R, then DR / DT is a point speed, expressed as a function of time. Differentiation over time again, we get acceleration. Suppose that the point moves along the curve shown in Fig. 10. Let S be a distance traveled by a point along the curve. During the small time interval, the DT point will pass DS distance along the curve; The position of the radius-vector will change to Dr. Therefore, DR / DS - vector directed as Dr. Further

Vector DR - changing the radius vector.

There is a single vector tangent to the curve. This is evident from the fact that when the point q is approached to the point P, PQ is approaching the tangent and DR approaches the DS. Formulas for differentiation of the product are similar to the formulas for differentiation of the product of scalar functions; However, since the vector product is anti-commutative, the multiplication order must be saved. Therefore,

Thus, we see that if the vector is the function of one scalar variable, then we can present the derivative almost as in the case of a scalar function.
Vector and scalar fields. Gradient. Physics often have to deal with vector or scalar values \u200b\u200bthat vary from point to point in a given area. Such areas are called "fields". For example, a scalar can be temperature or pressure; The vector can be the speed of moving fluid or electrostatic field of charge system. If we chose some coordinate system, then any point P (x, y, z) in a given area corresponds to some radius-vector R (\u003d xi + yj + zk) and also the value of the vector value U (R) or the scalar F (R) associated with it. Suppose that U and F are defined in the area definitely; those. Each point corresponds to one and only one value u or f, although different points can, of course, have different values. Suppose that we want to describe the speed with which u and f change when moving along this area. Simple private derivatives, such as DU / DX and DF / DY, do not suit us, because they depend on the specifically selected coordinate axes. However, you can enter a vector differential operator, independent of the choice of axes of coordinates; This operator is called "gradient". Let we deal with the scalar field f. First, as an example, consider the circuit card area of \u200b\u200bthe country. In this case, F is the height above sea level; Contour lines connect points with the same value f. When moving along any of these lines F does not change; If you move perpendicular to these lines, then the rate of change f will be maximum. We can compare each point by the vector indicating the value and direction of the maximum change in the speed F; Such a card and some of these vectors are shown in Fig. 11. If we do it for each point of the field, we obtain a vector field associated with a scalar field f. This is a vector field called "gradient" F, which is written as Grad F or CF (symbol C is also called "recruit").

In the case of three dimensions, the contour lines become surfaces. Small displacement DR (\u003d IDX + JDY + KDZ) leads to a change of F, which is written as

Where points indicate more than high orders. This expression can be written as a scalar product.

We divide the right and left parts of this equality on DS, and let DS tends to zero; then

where DR / DS is a single vector in the selected direction. Expression in parentheses - vector, depending on the selected point. Thus, the DF / DS has the maximum value when DR / DS indicates in the same direction, the expression that stands in brackets is a gradient. In this way,

- A vector equal to the value and coinciding in the direction with a maximum rate of change F relative to the coordinates. Gradient F is often written in the form

This means that the operator with exists by itself. In many cases, it behaves like a vector and is actually a "vector differential operator" - one of the most important differential operators in physics. Despite the fact that C contains single vectors I, j and k, its physical meaning does not depend on the selected coordinate system. What is the connection between the CF and F? First of all, suppose that F determines the potential anywhere. With any low displacement of the DR, the value of F will change to

If q is a value (for example, a mass, charge), displaced on DR, then the work performed when moving q to DR is equal to

Since Dr - Move, QCF - force; -Sf - tension (force per unit of quantity), associated with f. For example, let U be electrostatic potential; Then E is the electric field strength, is given by the formula E \u003d -CU. Suppose U is created by a point electric charge in Q of pendants placed at the beginning of the coordinates. The value of U at P (X, Y, Z) with a radius-vector R is given by the formula

Where E0 is a dielectric constant of free space. therefore

From where it follows that E acts in the direction R and its value is q / (4pe0R3). Knowing the scalar field, you can determine the associated vector field. It is also possible to reverse. From the point of view of mathematical processing, scalar fields are operated easier than the vector, since they are set by one coordinate function, while the vector field requires three functions corresponding to the components of the vector in three directions. Thus, the question arises: the vector field is given, can we record the associated scalar field?
Divergence and rotor. We saw the result of the action on the scalar function. What happens if with apply to the vector? There are two possibilities: let U (x, y, z) - vector; Then we can form a vector and scalar product as follows:

The first of these expressions is a scalar called divergence U (denoted by divu); The second is the vector, the named rotor U (denoted by ROTU). These differential functions, divergence and rotor are widely used in mathematical physics. Imagine that U is some vector and that it and its first derivatives are continuous in some area. Let p be a point in this area, surrounded by a small closed surface S that limits the volume of DV. Let N be a single vector, perpendicular to this surface at each point (n changes the direction when driving around the surface, but always has a single length); Let N be directed outward. Let's show that

Here s indicates that these integrals are taken over the entire surface, Da is the element of the surface S. For simplicity, we will choose a convenient form S in the form of a small parallelepiped (as shown in Fig. 12) with DX, DY and DZ sides; Point P is a parallelepiped center. We calculate the integral from equation (4) first on one face of parallelepiped. For the front edge n \u003d i (single vector parallel x axis); Da \u003d Dydz. Contribution to the integral from the front face is equal

On the opposite face n \u003d -i; This edge gives contribution to the integral

Using Taylor Theorem, we get a common contribution from two faces

Note that dxdydz \u003d dv. Similarly, you can calculate the contribution from the other other pairs of the facets. Full integral equal

And if we put DV (R) 0, then the members of a higher order will disappear. By formula (2), the expression in brackets is divu, which proves equality (4). Equality (5) can be proved in the same way. We use rice again. 12; Then the contribution from the front edge to the integral will be equal

And, using the Taylor theorem, we get that the total contribution to the integral from two faces has the form

those. These are two members from the expression for ROTU in equation (3). Other four members will work after accounting for contributions from other four faces. What, in essence, mean these relationships? Consider equality (4). Suppose u - speed (liquid, for example). Then nchu da \u003d un da, where un is the normal component of the vector U to the surface. Therefore, Un Da is the volume of fluid flowing through DA per unit of time, and is the volume of fluid flowing through S per unit of time. Hence,

Expansion rate of a unit of volume around the point P. From here, the divergence received its name; It shows the speed with which the liquid is expanding from (i.e. divergent from) P. To explain the physical value of the rotor U, consider another surface integral for a small cylindrical volume H height of H surrounding the point P; Flat-parallel surfaces can be oriented in any direction that we choose. Let k be a -sedine vector perpendicular to each surface, and let the area of \u200b\u200beach surface of the DA; Then the total volume DV \u003d HDA (Fig. 13). Consider now the integral

Finally I got hands to an extensive and long-awaited topic analytical geometry. First, a little about this section of the highest mathematics .... Surely you now remembered the course of school geometry with numerous theorems, their evidence, drawings, etc. What to hide, unloved and often an affordable subject for a significant share of students. Analytical geometry, oddly enough, may seem more interesting and affordable. What does the adjective "analytical" mean? Two stamped mathematical turnover immediately come to mind: "Graphic solution method" and "Analytical solution method". Graphic method, Clearly, is associated with the construction of graphs, drawings. Analyticalsame method assumes the solution of tasks predominantly By means of algebraic action. In this regard, the algorithm of solutions of almost all tasks of analytic geometry is simple and transparent, often enough to gently apply the necessary formulas - and the answer is ready! No, of course, quite without drawings here it will not cost, besides, for a better understanding of the material, I will try to bring them above the necessity.

The opening rate of lessons in geometry does not claim theoretical completeness, it is focused on solving practical tasks. I included in my lectures only that from my point of view is important in practical terms. If you need a more complete certificate according to any subsection, I recommend the following quite affordable literature:

1) The thing with which, without joke, is familiar to several generations: School textbook on geometry, authors - L.S. Atanasyan and the company. This hanger of school dressing room has already sustained the 20s (!) Reprint, which, of course, is not the limit.

2) Geometry in 2 volumes. Authors L.S. Atanasyan, Basilev V.T.. These are literature for higher education, you will need first Tom. From my field of view, rarely found tasks may fall out, and the textbook will provide invaluable assistance.

Both books can be downloaded for free on the Internet. In addition, you can use my archive with ready-made solutions that can be found on the page. Download examples of higher mathematics.

From instrumental tools I propose again my own development - software package According to analytical geometry, which will significantly simplify life and save a mass of time.

It is assumed that the reader is familiar with the basic geometric concepts and figures: point, direct, plane, triangle, parallelogram, parallelepiped, cube, etc. It is advisable to remember some theorems, at least the theorem of Pythagora, hello to 10th year)

And now we will consistently consider: vector concept, actions with vectors, vector coordinates. Next I recommend reading The most important article Scalar product vectorsas well as Vector and mixed artwork vectors. Local task is not too much - dividing the segment in this respect. Based on the above information, you can master direct equation on the plane from the simplest examples of solutionswhat will allow learn to solve geometry challenges. The following articles are also useful: Plane equation in space, Equations direct in spaceThe main tasks for the straight and plane, other sections of analytical geometry. Naturally, simultaneously consider typical tasks.

Vector concept. Free vector

First we repeat the school definition of the vector. Vector called directed The segment for which its beginning and the end is indicated:

In this case, the beginning of the segment is the point, the end of the segment - the point. The vector itself is indicated through. Direction It is essential if you rearrange the arrow to another end of the segment, then the vector will be, and this is already a completely different vector. The concept of the vector is convenient to identify with the movement of the physical body: you see, go to the door of the institute or get out of the door of the institute are completely different things.

Separate points of the plane, space is convenient to consider the so-called zero vector . In such a vector, the end and the beginning coincide.

!!! Note: Hereinafter, it can be considered that the vectors lie in the same plane or you can assume that they are located in the space - the essence of the outlined material is also valid for the plane and for space.

Designations: Many immediately drew attention to the wand without arrow in the designation and said, in the same time they put the arrow! True, you can write with the arrow: but allowed the record that I will use in the future. Why? Apparently, such a habit has developed from practical considerations, my arrows at school and university turned out to be too differentized and shaggy. In the educational literature, sometimes they do not bother with clocks at all, but allocate letters in bold:, implying that this is a vector.

That was the style, and now about the methods of recording vectors:

1) vectors can be written by two large Latin letters:
etc. At the same time the first letter before Indicates the beginning of the vector, and the second letter - the point-end vector.

2) Vectors also record small Latin letters:
In particular, our vector is possible for brevity to convert a small Latin letter.

Lena or module The nonzero vector is called the length of the segment. The length of the zero vector is zero. Logical.

The length of the vector is indicated by the sign of the module:

How to find the length of the vector We will learn (or repeat, for whom as) a little later.

That there were elementary information about the vector familiar to all schoolchildren. In the analytical geometry, the so-called free vector.

If it is simple - vector can be postponed from any point.:

We used to call such vectors (the definition of equal vectors will be given below), but is purely from a mathematical point of view. This is the same vector or free vector. Why free? Because during solving tasks, you can "attach" one or another vector in any, the point of the plane or space you need. This is a very cool property! Imagine an arbitrary length and directions - it can be "cloning" an infinite number of times and at any point of space, in fact, it exists everywhere. There is such a student surcharge: to each lector in f ** y via the vector. After all, not just a witty rhyme, everything mathematically correct - the vector can be attached there. But do not rush to rejoice, the students themselves suffer more often \u003d)

So, free vector - this is lots of identical directed segments. School definition of a vector given at the beginning of the paragraph: "The vector is called a directed cut ...", implies specific The directional segment taken from this set, which is tied to a certain point of the plane or space.

It should be noted that in terms of physics, the concept of free vector in the general case incorrectly, and the point of the vector application is important. Indeed, a direct blow of the same force on the nose or in the forehead is enough to develop my stupid example take different consequences. However, non-free Vectors meet and informed (do not go there :)).

Actions with vectors. Collinearity vectors

In the school year of geometry, a number of actions and rules with vectors are considered: addition of the rule of the triangle, addition according to the rule of the parallelogram, vector difference rule, vector multiplication by the number, scalar product of vectors, etc. For seed, we repeat two rules that are particularly relevant to solve the problems of analytical geometry.

The rule of the addition of vectors according to the rule of triangles

Consider two arbitrary nonzero vector and:

It is required to find the amount of these vectors. Due to the fact that all vectors are considered free, postpone vector from end Vector:

Sum of vectors and is vector. For a better understanding of the rule in it, it is advisable to invest physical meaning: let some body made a way to the vector, and then by the vector. Then the sum of the vectors is a vector of the resulting path with the beginning at the point of departure and the end at the arrival point. A similar rule is formulated for the amount of any number of vectors. As they say, the body can pass its way strongly from a zigzag, and maybe on autopilot - according to the resulting vector sum.

By the way, if the vector is postponed from start vector, then it will be equivalent pollogram rule Addition of vectors.

First about the collinearity of vectors. Two vectors are called collinearif they lie on one straight line or on parallel straight lines. Roughly speaking, we are talking about parallel vectors. But in relation to them, adjective "collinear" always use.

Present two collinear vector. If the arrow of these vectors are directed in the same direction, then such vectors are called sonated. If the arrows look in different directions, then the vectors will the oppositely directed.

Designations: The collinearity of the vectors are recorded with the usual parallelism icon: it is possible to detail: (the vectors are coated) or (vectors are opposite).

Work The nonzero vector on the number is such a vector, the length of which is equal, and the vectors and are coated with the oppositely directed at.

The vector multiplication rule is easier to understand with the drawing:

We understand more detail:

1) direction. If the multiplier is negative, then vector changes the direction On the opposite.

2) Length. If the multiplier is concluded within or, then the length of the vector decreases. So, vector length is two times less than the length of the vector. If the multiplier module is more than one, then the length of the vector increases in time.

3) Note that all collinear vectorsIn this case, one vector is expressed through another, for example. The opposite is also fair: If one vector can be expressed through the other, then such vectors necessarily collinear. In this way: if we multiply the vector to the number, then the collinear (in relation to the initial) vector.

4) The vectors are coated. Vectors and are also coated. Any of the first group of the first group is oppositely directed towards any second group vector.

What vectors are equal?

Two vectors are equal if they are coinled and have the same length.. Note that the cooler implies the collinearity of the vectors. The definition will be inaccurate (redundant) if you say: "Two vectors are equal if they are collinear, are coated and have the same length."

From the point of view of the concept of free vector, equal vectors are the same vector, which already happened in the previous paragraph.

The coordinates of the vector on the plane and in space

First point Consider vectors on the plane. I will depict the Cartesian rectangular coordinate system and postpone from the beginning of the coordinates single Vectors and:

Vectors I. orthogonal. Orthogonal \u003d perpendicular. I recommend that slowly get used to the terminas: instead of parallelism and perpendicularity, we use words accordingly collinearity and orthogonality.

Designation: The orthogonality of vectors are recorded by the usual perpendicularity icon, for example :.

The vectors under consideration are called coordinate vectors or orthy. These vectors form basis on surface. What is the basis, I think, intuitively many understandable, more detailed information can be found in the article. Linear (not) vector dependence. Basis vectors. Surrentible words, the basis and the beginning of the coordinates set the entire system - this is a kind of foundation on which a complete and saturated geometric life boils.

Sometimes built base called ortonormated The basis of the plane: "Orto" - because the coordinate vectors are orthogonal, the adjective "normalized" means one, i.e. The length of the base vectors are equal to one.

Designation: Basis is usually recorded in parentheses inside which in strict sequence Listed basic vectors, for example:. Coordinate vectors it is impossible Rearrange in places.

Any Vector plane the only way expressed in the form:
where - numberscalled coordinates of the vector In this base. And the expression itself called decomposition of vector Basisus .

Dinner served:

Let's start with the first letter of the alphabet :. According to the drawing, it is clearly seen that when the vector decomposition of the basis, just considered:
1) vector multiplication rule by number: and;
2) Addition of vectors of the triangle rule :.

And now mentally set the vector from any other point of the plane. It is clear that his decomposition will be "relentlessly follow him." Here it is, the freedom of the vector - the vector "all wears with you." This property, of course, is true for any vector. It's funny that the basic (free) vectors are not necessary to postpone from the beginning of the coordinates, one can draw, for example, to the left at the bottom, and the other is on the right above, and nothing will change! True, it is not necessary to do so, because the teacher will also show originality and draws you "credited" in an unexpected place.

Vectors, illustrate exactly vector multiplication rule by number, vector is co-directed with a basic vector, the vector is directed opposite to the base vector. The data of the vectors are one of the coordinates is zero, it can be recorded that:

And the basic vectors, by the way, so: (in fact, they are expressed themselves through themselves).

And finally: ,. By the way, what is the subtraction of vectors, and why didn't I told about the deduction rule? Somewhere in a linear algebra, I do not remember where, I noted that subtraction is a special case of addition. So, the decomposition of the vectors "DE" and "E" are quietly recorded in the form of the amount: . Rearrange the components of the places and follow the drawing, as the old good addition of vectors according to the rule of triangle works clearly in these situations.

Considered decomposition of type Sometimes called the decomposition of the vector in the ort system (i.e. in the system of single vectors). But this is not the only way to record the vector, the following option is distributed:

Or with the sign of equality:

The basic vectors themselves are written as follows: and

That is, in parentheses, the coordinates of the vector are indicated. In practical tasks, all three recording options are used.

Doubted whether to say, but still I will say: the coordinates of the vectors cannot be rearranged. Strictly in the first place write down the coordinate that corresponds to the unit vector strictly in second place We write down the coordinate that corresponds to the unit vector. Indeed, and - this is because two different vector.

Coordinates on the plane figured out. Now consider the vectors in three-dimensional space, here almost all the same! Only add another coordinate. Three-dimensional drawings perform hard, so I will limit the same vector, which for simplicity will postpone from the start of the coordinates:

Any Vector three-dimensional space can single way Scroll through the orthonormal basis:
, where - the coordinates of the vector (numbers) in this base.

Example from the picture: . Let's see how the rules of action with vectors work here. First, the multiplication of the vector is: (Red Arrow), (Green Arrow) and (Raulic Arrow). Secondly, an example of adding a few, in this case three, vectors :. The vector of the amount begins at the starting point of the departure (beginning of the vector) and stuck in the final point of arrival (end vector).

All three-dimensional vectors are naturally free, try mentally to postpone the vector from any other point, and you will understand that his decomposition will remain with it. "

Similar to flat case, in addition to recording Versions with brackets are widely used: either.

If there is no one (or two) coordinate vector in the decomposition, then zeros are put instead. Examples:
Vector (meticulous ) - write;
Vector (meticulous ) - write;
Vector (meticulous ) - We write.

Base vectors are written as follows:

This is perhaps all the minimum theoretical knowledge necessary to solve the problems of analytical geometry. Perhaps a bit of terms and definitions, so I recommend to re-read the teapots and comprehend this information again. And any reader will be useful from time to time to contact the basic lesson for better mastering the material. Collinearity, orthogonality, orthonormal basis, decomposition of a vector - these and other concepts will often be used in the future. I note that the materials of the site are not enough to pass the theoretical test, colloquium on geometry, since all the theorems (moreover without evidence) I carefully encrypt - to the detriment of the scientific style of the presentation, but plus to your understanding of the subject. To obtain a detailed theoretical reference, I ask for a bow to Professor Atanasyan.

And we turn to the practical part:

The simplest tasks of analytical geometry.
Actions with vectors in coordinates

Tasks that will be considered is extremely desirable to learn to solve on a complete machine, and formulas remember HolyEven especially not to memorize themselves, they will remember \u003d) This is very important because other tasks of analytical geometry are based on the simplest elementary examples, and will annoy the extra time for eating pawns. No need to flash the upper buttons on the shirt, many things are familiar with you from school.

The presentation of the material will go parallel to the plane, and for space. For the reason that all formulas ... See themselves.

How to find a vector on two points?

If two planes points are given and, the vector has the following coordinates:

If there are two points of space and, the vector has the following coordinates:

I.e, from vector end coordinates need to deduct the corresponding coordinates beginning of the vector.

The task: For the same points, write down the formula of finding the coordinates of the vector. Formulas at the end of the lesson.

Example 1.

There are two points of the plane and. Find the coordinates of the vector

Decision: According to the corresponding formula:

Alternatively, you could use the following entry:

Aesthetes are solved as follows:

Personally, I used to the first version of the recording.

Answer:

By condition, it was not necessary to build a drawing (which is typical for the tasks of analytical geometry), but in order to explain some moments to teapots, do not fit:

Be sure to understand the difference between the coordinates of the points and the coordinates of the vectors:

The coordinates of the point - These are the usual coordinates in the rectangular coordinate system. Saving points on the coordinate plane, I think everyone is able to still from 5-6 class. Each point has a strict place on the plane, and move them somewhere cannot be moved.

Coordinates of the same vector - This is his basis on the basis, in this case. Any vector is free, so if necessary, we can easily postpone it from some other point of the plane. Interestingly, for vectors you can not build axis at all, the rectangular coordinate system, only the basis is needed, in this case the orthonormal basis of the plane.

Records of the coordinates of the points and the coordinates of the vectors seems to be similar:, and the meaning of the coordinates absolutely differentAnd you should understand this difference well. This difference, of course, is valid for space.

Ladies and gentlemen, get hand:

Example 2.

a) donated points and. Find vectors and.
b) donas and. Find vectors and.
c) dates and. Find vectors and.
d) dates. Find verses .

Perhaps enough. These are examples for an independent solution, try not to neglect them, pay off ;-). Drawings do not need to do. Solutions and answers at the end of the lesson.

What is important when solving tasks of analytical geometry? It is important to be extremely attentive to prevent the workshop of the error "two plus two is equal to zero." I immediately apologize if I was wrong \u003d)

How to find a length of a segment?

Length, as already noted, is indicated by the module sign.

If two points of the plane are given and, then the length of the segment can be calculated by the formula

If there are two points of space and, then the length of the segment can be calculated by the formula

Note: Formulas will remain correct if relevant coordinates are rearranged by places: and, but more standard is the first option.

Example 3.

Decision: According to the corresponding formula:

Answer:

For clarity, I will perform a drawing

Section - this is not vectorand move it somewhere, of course, it is impossible. Also, if you perform a drawing on a scale: 1 unit. \u003d 1 cm (two airtal cells), then the resulting answer can be checked by a conventional line, directly measuring the length of the segment.

Yes, the solution is short, but there is still a couple of important moments that I would like to clarify:

First, in response, we put the dimension: "Units". The condition does not say that it is millimeters, centimeters, meters or kilometers. Therefore, a mathematically competent solution will be a general formulation: "units" - abbreviated "units".

Secondly, we repeat the school material that is useful not only for the considered task:

pay attention to important technical technique – plugging from under the root. As a result of the calculations, we had a result and a good mathematical style involves making a factor from under the root (if possible). More The process looks like this: . Of course, to leave the answer in the form will not be an error - but the deficient thing is for sure and the weighty argument for the soldiers from the teacher.

Here are other common cases:

Often, under the root, a sufficiently large number is obtained, for example. How to be in such cases? In a calculator, check whether a number is divided into 4:. Yes, it was divided, thus divided: . Or maybe the number once again will be divided into 4? . In this way: . In the number the last figure is odd, therefore, divided for the third time in 4 it is clearly not possible. We try to divide nine :. As a result:
Ready.

Output: If the number is at the root, the number is obtained, then we are trying to endure a multiplier from under the root - on the calculator we check whether the number is divided by: 4, 9, 16, 25, 36, 49, etc.

During the solution of various problems, the roots are often found, always try to extract multipliers from under the root in order to avoid a lower assessment of yes unnecessary problems with the improvement of your decisions according to the teacher's comment.

Let's at the same time we repeat the construction of the roots into the square and other degrees:

The rules of action with degrees in general can be found in the school textbook on algebra, but I think, from the above examples, everything or almost everything is already clear.

Task for an independent solution with a segment in space:

Example 4.

Dana dots and. Find the length of the segment.

Solution and answer at the end of the lesson.

How to find the length of the vector?

If a vector plane is given, its length is calculated by the formula.

If the vector of space is given, its length is calculated by the formula .

In this article, we will start a discussion of one "chopstice sticks", which will allow you to reduce many geometry tasks for simple arithmetic. This "stick" can significantly ease your life especially in the case when you are insecably feel in the construction of spatial figures, sections, etc. All this requires a certain imagination and practical skills. Method, which we will begin to consider here, will allow you to almost completely abstract from all kinds of geometric constructions and reasoning. The method is called "Coordinate method". In this article, we will consider the following questions:

Coordinate plane
Points and vectors on the plane
Building a vector along two points
Vector length (Distance between two points)
Coordinates of the middle of the cut
Scalar product vectors
Corner between two vectors

I think you have already guessed why the coordinate method is so called? True, it received such a name, as it operates not with geometric objects, but with their numerical characteristics (coordinates). And the conversion itself, which allows you to move from geometry to algebra, is to introduce the coordinate system. If the source figure was flat, then the coordinates are two-dimensional, and if the formation figure, then the coordinates are three-dimensional. In this article we will consider only a two-dimensional case. And the main purpose of the article is to teach you to use some basic techniques of the coordinate method (they are sometimes useful in solving problems in planimetry in the USE part B). The following two sections on this subject are devoted to discussing the same methods for solving problems of Tasks C2 (task for stereometry).

Why would it be logical to start discussing the method of coordinates? Probably, with the concept of the coordinate system. Remember when you with her first encountered. It seems to me that in grade 7, when you learned about the existence of a linear function, for example. Let me remind you, you built it at points. Do you remember? You chose an arbitrary number, substituted it in the formula and calculated in this way. For example, if, then, if, then, etc., what did you get in the end? And I received a point with the coordinates: and. Next, you painted the "cross" (coordinate system), chose a scale on it (how many cells you will have a single segment) and noted on it the points received, which then combined the straight line, the resulting line and there is a function graph.

There are several moments that should be explained to you a little more:

1. A single segment you choose for reasons convenience, so that everything is beautiful and compactly fit in the picture

2. It is accepted that the axis goes left to right, and the axis is to the bottom

3. They intersect at right angles, and the point of their intersection is called the beginning of the coordinates. It is indicated by the letter.

4. In the recording of the coordinates of the point, for example, on the left in brackets there is a point coordinate along the axis, and on the right, along the axis. In particular, simply means that the point

5. In order to set any point on the coordinate axis, it is required to specify its coordinates (2 numbers)

6. For any point lying on the axis,

7. For any point lying on the axis,

8. The axis is called the abscissa axis

9. The axis is called the ordinate axis

Now let's make the next step with you: We note two points. Connect these two points with a segment. And put the arrow as if we spend a segment from point to point: That is, we will make our segment directed!

Remember how else the directed segment is called? True, it is called a vector!

Thus, if we connect a point with a point, moreover, we will have a point A, and the end - point B, then we get a vector. Did you make this building too in grade 8, remember?

It turns out that vectors, like the points, can be denoted by two numbers: these numbers are called vector coordinates. Question: Do you think it is enough for us to know the coordinates of the beginning and end of the vector to find its coordinates? It turns out that yes! And it is done very simple:

Thus, since the dot vector is the beginning, and the end, the vector has the following coordinates:

For example, if, the coordinates of the vector

Now let's do on the contrary, we will find the coordinates of the vector. What should we change for this? Yes, you need to swap the beginning and end: now the beginning of the vector will be at the point, and the end is at the point. Then:

Look carefully, what is the difference between the vectors and? Their only difference is signs in coordinates. They are opposite. This fact is accepted to record like this:

Sometimes, if it is not specifically stipulated, which point is the beginning of the vector, and how end, the vectors are denoted by two capital letters, but one line, for example:, etc.

Now a little penate And find the coordinates of the following vectors:

Check:

And now deciding a problem a little more complicated:

A century with on-cha-scrap at the point has a co-or-di-on-you. NAI-DITE ABS CISS DOP.

All the same is pretty prose: Let the coordinates of the point. Then

I am a system to determine what the coordinates of the vector. Then the point has coordinates. We are interested in the abscissa. Then

Answer:

What else can you do with vectors? Yes, almost all the same as with ordinary numbers (unless you can not divide, it is possible to multiply in two ways, one of which we will discuss here a little later)

Vectors can be folded with each other
Vectors can be deducted from each other
Vectors can be multiplied (or divide) on an arbitrary nonzero number
Vectors can be multiplied by each other

All these operations have a completely visual geometric representation. For example, a rule of a triangle (or a parallelogram) for addition and subtraction:

The vector is stretched or compressed or changes the direction when multiplying or dividing by:

However, here we will be interested in the question of what is happening with the coordinates.

1. When adding (subtracting) of two vectors, we fold (deduct) alternately their coordinates. I.e:

2. When multiplying (division) of the vector by number, all its coordinates are multiplied (divided) to this number:

For example:

· Nay-die the sum of the co-or-di-nat's eyelid.

Let's first find the coordinates of each of the vectors. Both of them have the same start - the point of the origin. They have different ends. Then. Now we calculate the coordinates of the vector then the sum of the coordinates of the resulting vector is equal.

Answer:

Now the following task is:

· Find the sum of the coordinates of the vector

Check:

Let's consider now the following task: we have two points on the coordinate plane. How to find the distance between them? Let the first point be, and the second. Denote the distance between them through. Let's make the following drawing for clarity:

What I've done? First, I, first, connected points and, and also spent the line from the point, parallel to the axis, and spent the line from the point parallel to the axis. Have they crossed at the point by forming a wonderful figure? What is it wonderful? Yes, we are almost just knowing about the rectangular triangle. Well, the theorem of Pythagora - for sure. The desired segment is the hypotenuse of this triangle, and the segments are kartettes. What are the coordinates of the point? Yes, it is easy to find them in the picture: since the segments are parallel to the axes and, accordingly, their lengths are easy to find: if you designate the length of the segments, respectively, then

Now we use the Pythagorean theorem. We know the length of the cathets, we will find hypotenuse:

Thus, the distance between two points is the root of the sum of the squares of differences from the coordinates. Or - the distance between two points is the length of the segment, which connects them. It is easy to notice that the distance between points does not depend on the direction. Then:

From here we make three outputs:

Let's take a little exercise in the calculation of the distance between the two points:

For example, if, then the distance is between and equal

Or let's go differently: we find the coordinates of the vector

And find the length of the vector:

As you can see, the same thing!

Now practice a little:

Task: find the distance between the specified points:

Check:

Here is another pair of tasks on the same formula, though they sound a little different:

1. Nay-di KVAD-RAT of the length of the eyelid.

2. NAY-Di KVAD-RAT of the length of the eyelid-ra

I think so, did you easily manage with them? Check:

1. And this is at the attentiveness) we have already found the coordinates of the vectors and earlier :. Then the vector has coordinates. The square of its length will be equal to:

2. Find the vector coordinates

Then the square of its length is equal

Nothing difficult, right? Ordinary arithmetic, no more.

The following tasks cannot be classified unambiguously, they are more like a general erudition and to draw simple pictures to the ability.

1. Nay-di sinus angle of the corner of the na-klo-on from-cut, co-unit-in-y-th point, with an abscissa axis.

and

How will we come here? It is necessary to find the sine angle between and axis. And where do we know how to look for sinus? True, in a rectangular triangle. So what do we need to do? Build this triangle!

Since the coordinates of the point and, then the segment is equal, and the segment. We need to find a sine corner. I will remind you that sinus is the attitude of the opposite catech for the hypotenuse, then

What do we have to do? Find hypotenuse. You can do it in two ways: according to the Pythagore Theorem (katenets are known!) Or by the distance formula between the two points (actually the same thing as the first way!). I will go secondly:

Answer:

The next task will seem to you even easier. She is on the coordinates of the point.

Task 2. From the point of Oposchn Pen-Pen-Di-Liar on the ABS axis. NAI-DITE ABS CIS-SU OS-NO-VIA-PEN-DI-KU-LA-RA.

Let's make a drawing:

The base of the perpendicular is the point in which it crosses the abscissa axis (axis) is the point. Figure shows that it has coordinates :. We are interested in the abscissa - that is, the "ounce" component. It is equal.

Answer: .

Task 3. Under the conditions of the previous task, find the amount of distance from the point to the coordinate axes.

The task is generally elementary if you know what is the distance from the point to the axes. You know? I hope, but still remind you of:

So, on my drawing, located just above, I have already portrayed one such perpendicular? What is the axis? To the axis. And what is the length of his length then? It is equal. Now I have a perpendicular to the axis and find it length. It will be equal, right? Then their amount is equal.

Answer: .

Task 4. In terms of problems 2, find the order of the point, the symmetrical point relative to the abscissa axis.

I think you are intuitively clear what symmetry is? Very many objects it possess: many buildings, tables, airplanes, many geometric shapes: ball, cylinder, square, rhombus, etc. Roughly speaking, symmetry can be understood as: the figure consists of two (or more) the same halves. Such symmetry is called axial. What then is the axis? This is the same line in which the figure can, relatively speaking, "cut" on the same halves (in this picture the axis of symmetry is straight):

Now let's go back to our task. We know that we are looking for a point, symmetric about the axis. Then this axis is the symmetry axis. So we need to mention such a point so that the axis can cut the segment into two equal parts. Try yourself to celebrate such a point. And now compare with my decision:

Did you do the same? Okay! At the found point we are interested in ordinary. It is equal

Answer:

And now tell me, thinking seconds, what will the abscissa point, the symmetrical point A relative to the ordinate axis? What is your answer? Correct answer: .

In the general case, the rule can be written like this:

The point, symmetric point relative to the abscissa axis, has coordinates:

Point, symmetrical point relative to the ordinate axis, has coordinates:

Well, now quite terrible a task: Find the coordinates of the point, symmetric point, relative to the start of the coordinates. At first, think about yourself, and then look at my drawing!

Answer:

Now Pollogram problem:

Task 5: Points of Java-Way-Sia Ver-Shi-na Parale-le-Lo Gram Ma. Nay-die or-di-on-point.

You can solve this problem in two ways: the logic and method of coordinates. I first apply the coordinate method, and then I will tell you how to solve otherwise.

It is clear that the abscissa point is equal. (It lies on a perpendicular conducted from the point to the abscissa axis). We need to find ordinate. We use the fact that our figure is a parallelogram, it means that. Find the length of the segment using the distance formula between the two points:

Lower the perpendicular connecting the point with the axis. The intersection point will indicate the letter.

The length of the segment is equal. (Find the task itself, where we discussed this moment), then we find the length of the segment on the Pythagora theorem:

The length of the segment - exactly coincides with its ordinate.

Answer: .

Another solution (I'll just give a picture that illustrates it)

Solution:

1. Conduct

2. Find the coordinates of the point and length

3. Prove that.

One more cut length problem:

Points of Java-lyube-Sia Ver-Shi-on-Mi Tre-Coal-Ni. Nai di the length of its medium line, Parale-Lelle.

Do you remember what is the middle line of the triangle? Then for you this task is elementary. If you do not remember, I will remind you: the middle line of the triangle is a line that connects the mid-opposite sides. It is parallel to the base and is equal to half a half.

The base is a segment. Its length we had to look earlier, it is equal. Then the length of the middle line is half smaller and equal.

Answer: .

Comment: This task can be solved in another way to which we turn a little later.

In the meantime, now you have a few tasks, take off on them, they are completely simple, but help "fill the hand", on the use of the coordinate method!

1. Points of Java-La-Sia Ver-Shi-on-Tour-Pennation. Nai ds the length of its environment line.

2. Points and Java-Wa-Sia Ver-Shi-na Parale-le-Lo Gram Ma. Nay-die or-di-on-point.

3. Nay-di length from cut-ka, co-unit-ny-y-th point and

4. Nai di-tures of the Krai-shan-like f-gu-ry on the co-or-di-nu flat-co-po.

5. Surrounding with a price-troom in the on-cha-le co-or-di-nat Pro-Ho-dit through the point. Nay-di her ra di-musty.

6. NAY-DI-DI-DI-SCHIE-NO-POCI, OPI-SAN-NOE ROD-MO-COMPUT-NI-KA, VER-ShI-RO-RO -Di-on-you co-from-vet

Solutions:

1. It is known that the middle line of the trapezium is equal to half the base. The base is equal, and the base. Then

Answer:

2. The easiest way to solve this task is: notice that (the rule of the parallelogram). Calculate the coordinates of the vectors and is not possible :. In addition, the coordinate vectors are folded. Then has coordinates. The same coordinates also have a point, since the beginning of the vector is a point with coordinates. We are interested in ordinate. It is equal.

Answer:

3. We act right away by the distance formula between the two points:

Answer:

4. Look at the picture and say, between which two figures "clamped" the shaded region? It is clamped between two squares. Then the area of \u200b\u200bthe desired figure is equal to the square of a large square minus the square is small. The side of a small square is a segment connecting points and its length is equal

Then the small square square is equal

Similarly, with a big square: his side is a segment connecting points and its length is equal

Then the large square square is equal

Place the desired figure will find by the formula:

Answer:

5. If the circle has the origin as a center and passes through the point, its radius will exactly equal to the length of the segment (make a drawing and you will understand why it is obvious). Find the length of this segment:

Answer:

6. It is known that the radius of the circumference described near the rectangle is equal to half of its diagonal. We will find the length of any of two diagonals (after all, in a rectangle they are equal!)

Answer:

Well, you coped with everything? It was not very difficult to figure out, because so? The rule here is one thing - to be able to make a visual picture and simply "count" from it all the data.

We left quite a bit. There are still literally two points that I would like to discuss.

Let's try to decide this is such a simple task. Let two points and. Find the coordinates of the middle of the segment. The solution to this task is the following: Let the point - the search for the middle, then coordinates:

I.e: the coordinates of the middle of the segment \u003d the arithmetic average of the corresponding coordinates of the ends of the segment.

This rule is very simple and as a rule does not cause difficulties in students. Let's see what tasks and how it is used:

1. Nay-di or-di-on-tu se-di-di from-cut, co-unit-ny-yu-th point and

2. Points of Java-lyube-Sia Ver-Shi-na-mi-twh-coal-ni-ka. Nay-di or-di-on-ta dots of his di-go-on-lei.

3. Nai-di ABS-SU-SU price-tra surroundings of the neighborhood, opi-san-san near the right-Mo-Ni-ka, the Ver-Shi-RO Co-or-di-on-you co-ot-vet.

Solutions:

1. The first task is just a classic. We act immediately by definition of the middle of the segment. It has coordinates. Ordinate is equal.

Answer:

2. It is easy to see that this quadrilateral is a parallelogram (even rhombus!). You yourself can prove it yourself, the calculation of the length of the parties and comparing them between themselves. What do I know about parallelograms? His diagonal point of intersection is divided in half! Yeah! So the point of intersection of diagonals is what? This is a middle of any of the diagonals! Select, in particular, diagonal. Then the point has the coordinates of the ordinate point equal.

Answer:

3. What is the coincidence of the center described near the Circle Rectangle? It coincides with the intersection point of his diagonals. And what do you know about the diagonal of the rectangle? They are equal and the intersection point is divided by half. The task was drove to the previous one. I will take, for example, diagonal. Then if the center of the described circle, then the middle. Looking for coordinates: Absissal is equal.

Answer:

Now practice a little alone, I will only give answers to each task so that you can check yourself.

1. NAY-DI-TE-DI-SCHIE-NO-EI, opi-san about Tre-coal-ni-ka, Ver-Shi-GO-RO have co-or-di -no misters

2. NAY-DI-TE-DI-OU-TU-TUR DISCIEMBER-NOES, OPI-SAN-NOE PROTAGE-NI-KA, VER-Shi-GO-RO have coordinates

3. Ka-Ko-go-di-u-sa must-on being surrounded with a price-triple at point so that she can sa-las axis ABS?

4. Na-di or-di-on-ta dots of the axis of the axis and from-cut, the co-unit-yu-th point and

Answers:

Everything succeeded? I really hope for it! Now - the last jerk. Now be especially attentive. The material that I will now explain now is directly related not only to simple tasks on the coordinate method from b of the part, but also occurs everywhere in the task C2.

Which of my promises I have not yet restrained? Remember what operations on vectors I promised to enter and what ultimately introduced? I did not forget exactly? Forgot! I forgot to explain what the multiplication of vectors means.

There are two ways to multiply vector on the vector. Depending on the selected method, we will have objects of different nature:

Vector product is performed pretty cunning. How to do it and why it is necessary, we will discuss in the next article. And in this we will focus on the scalar product.

There are already two ways to allow us to calculate:

As you guessed, the result should be the same! So, let's first consider the first way:

Scalar product through coordinates

Find: - generally accepted indication of a scalar product

Formula for calculation Next:

That is, the scalar product \u003d the amount of the works of the coordinates of the vectors!

Example:

Nai di

Decision:

We will find the coordinates of each of the vectors:

Calculate the scalar product by the formula:

Answer:

See, absolutely nothing complicated!

Well, now try myself:

· Nay-di SKA-LAR-NEE pro-from-ve-de -ity of events and

Cope? Maybe I noticed the trick small? Let's check:

The coordinates of the vectors as in the past task! Answer:.

In addition to the coordinate, there is another way to calculate a scalar product, namely, through the lengths of vectors and cosine angle between them:

Indicates the angle between the vectors and.

That is, the scalar product is equal to the product of the lengths of the vectors on the cosine of the corner between them.

Why do we have this second formula if we have the first one that is much easier, there are at least no cosine in it. And it is necessary for the fact that from the first and second formula we can withdraw how to find the angle between vectors!

Let then remember the formula for the length of the vector!

Then if I substitute this data in the formula of the scalar product, then I will get:

But on the other side:

So what did I get to you? We now have a formula that allows you to calculate the angle between two vectors! Sometimes it is also written for brevity as follows:

That is, the algorithm for calculating the angle between the vectors is as follows:

Calculate the scalar product through the coordinates
We find the length of the vectors and turn them out
We divide the result of clause 1 on the result of clause 2

Let's practice in the examples:

1. Nay-di the corner between the eyelid-ray and. Give the answer in gra-du-sac.

2. Under the conditions of the previous task, find the cosine between the vectors.

We will do this: the first task I will help you decide, and try to do the second yourself! I agree? Then begin!

1. These vector are our old familiar. We already considered their scalar work and it was equal. They have such coordinates :, Then we find their lengths:

Then we are looking for a cosine between vectors:

Kosinus which corner is equal? This is the angle.

Answer:

Well, now I myself solve the second task, and then compare! I will give only a very brief decision:

2. It has coordinates, has coordinates.

Let - the angle between the vectors and, then

Answer:

It should be noted that the tasks are directly in the vector and the coordinate method in the part b of the examination work is rather rare. However, the overwhelming majority of C2 tasks can be easily solved by resorting to the introduction of the coordinate system. So you can consider this article by the foundation, on the basis of which we will make enough tricky construction, which will be needed to solve complex tasks.

Coordinates and vectors. Middle roving

We continue to study the coordinate method. In the last part, we brought a number of important formulas that allow:

Find the coordinates of the vector
Find the vector length (alternative: distance between two points)
Fold, subtract vectors. Multiply them to real number
Find a middle cut
Calculate the scalar product of vectors
Find angle between vectors

Of course, the entire coordinate method does not fit into these 6 points. It underlies such science as an analytical geometry with which you have to get to know the university. I just want to build a foundation that will allow you to solve problems in a single state. Exam. With the tasks of the part B we figured out in now it's time to go to a qualitatively new level! This article will be devoted to the method of solving those C2 tasks, in which it will be reasonable to move to the coordinate method. This rationality is determined by the fact that the task is required to find and which figure is given. So, I would apply the coordinate method if you are issued:

Find the angle between two planes
Find the angle between the straight and plane
Find the angle between two straight
Find the distance from the point to the plane
Find the distance from point to direct
Find the distance from the line to the plane
Find the distance between two straight

If the figure in the condition of the problem is the body of rotation (ball, cylinder, cone ...)

Suitable figures for the coordinate method are:

Rectangular parallelepiped
Pyramid (triangular, quadrangular, hexagonal)

Also in my experience it is impractical to use the coordinate method for:

Looking for areas of sections
Calculations of volumes

However, it should be immediately noted that three "unprofitable" for the method of coordinate situation in practice is quite rare. In most tasks, he can become your Savior, especially if you are not very strong in three-dimensional buildings (which sometimes are quite intricate).

What are all the above figures? They are no longer flat, such as, for example, a square, triangle, circle, and bulk! Accordingly, we need to consider not a two-dimensional, but a three-dimensional coordinate system. It is built fairly easy: just besides the axis of the abscissa and ordinates, we introduce another axis, the appliquet axis. The figure schematically shows their mutual location:

All of them are mutually perpendicular, intersect at one point, which we will call the start of coordinates. The axis of the abscissa, as before, we denote the axis of the ordinate - and the introduced axis of the application -.

If earlier each point on the plane was characterized by two numbers - abscissa and ordinary, then each point in space is already described by three numbers - abscissa, ordinate, applikate. For example:

Accordingly, the abscissa of the point is equal, ordinate -, and the applicatis -.

Sometimes the abscissa point is also called the projection of the point on the abscissa axis, the ordinate - the projection of the point on the axis of the ordinate, and the application - the projection of the point on the appliquet axis. Accordingly, if the point is set, the point with the coordinates:

call the projection point to the plane

Natural question arises: Are all formulas derived for a two-dimensional case in space? The answer is affirmative, they are fair and have the same look. For a small detail. I think you have already guessed yourself for which one. In all formulas, we must add another member responsible for the appliquet axis. Namely.

1. If two points are set: then:

Coordinates of the vector:
Distance between two points (or length of the vector)
The middle of the segment has coordinates

2. If two versions are given: and then:

Their scalar product is:
Cosine angle between vectors is:

However, the space is not so simple. As you understand, adding another coordinate makes a significant variety in the spectrum of figures, "living" in this space. And for further narration, I need to introduce some, roughly speaking, "generalization" straight. This "generalization" will be plane. What do you know about the plane? Try to answer the question, and what is a plane? It is very difficult to say. However, we all intuitively imagine how it looks like:

Roughly speaking, this is a non-infinite "leaf", covered in space. "Infinity" should be understood that the plane applies to all directions, that is, its area is equal to infinity. However, this explanation "on the fingers" does not give the slightest idea of \u200b\u200bthe structure of the plane. And it will be interested in it.

Let's remember one of the main axes of geometry:

through two different points on the plane, it goes straight, with just one:

Or its analogue in space:

Of course, you remember how to remove the equation directly in two predetermined points: if the first point has coordinates: and the second, then the direct equation will be as follows:

That you passed in the 7th grade. In the space, the direct equation looks like this: let us give two points with coordinates :, the equation is straight, through them passing, has the appearance:

For example, through points, the straight line passes:

How should it be understood? This should be understood as: the point lies on the line if its coordinates satisfy the following system:

We will not really be interested in the equation straight, but we need to pay attention to the very important concept of the direct vectors. - Any nonzero vector lying on this direct or parallel to it.

For example, both vectors are guide vectors direct. Let the point lying on the line, and its guide vector. Then the equation direct can be written in the following form:

I repeat once again, I will not be very interested in the equation straight, but I really need you to remember what the guide vector is! Again: this is any nonsense vector lying on a straight line, or parallel to it.

Display the equation of the plane for three specified points Not so trivially, and usually this question is not considered aware of high school. And in vain! This technique is vital when we resort to the coordinate method for solving complex tasks. However, I assume that you are full of desire to learn something new? Moreover, you can hit your teacher at the university when it turns out that you already know how you are already with a technique that is usually studied in the course of analytical geometry. So, proceed.

The plane equation is not too different from the direct equation on the plane, namely it looks:

some numbers (not all equal zero), and variables, for example: etc. As you can see, the equation of the plane is not very different from the equation of the straight line (linear function). However, remember that we have argued with you? We said that if we have three points that are not lying on one straight line, the equation of the plane is definitely restored by them. But how? I will try to explain to you.

Since the plane equation is:

And the points belong to this plane, then when substituting the coordinates of each point to the plane equation, we must receive a true identity:

Thus, it becomes necessary to solve three equations already with unknown! Dilemma! However, it can always be assumed that (for this you need to divide on). Thus, we obtain three equations with three unknowns:

However, we will not solve such a system, and we will divert the mysterious expression that follows from it:

The equation of the plane passing through three setpoints

\\ [\\ left | (\\ begin (array) (* (20) (C)) (x - (x_0)) & ((x_1) - (x_0)) & ((x_2) - (x_0)) \\\\ (y - (y_0) ) & ((y_1) - (y_0)) & ((y_2) - (y_0)) \\\\ (z - (z_0)) & ((z_1) - (z_0)) & ((z_2) - (z_0)) \\ END (Array)) \\ Right | \u003d 0 \\]

Stop! What else is what? Some very unusual module! However, the object that you see in front of yourself has nothing to do with the module. This object is called the third order determinant. From now on, in the future, when you are dealing with the coordinate method on the plane, you will very often meet these identifies. What is the third order determinant? Oddly enough, it is just a number. It remains to understand what specifically the number we will compare with the determinant.

Let's first write the third order determinant in a more general form:

Where are some numbers. And under the first index, we understand the line number, and under the index - the number of the column. For example, it means that this number is at the intersection of the second line and the third column. Let's raise the following question: How exactly will we calculate such a determinant? That is, what specific number will we compare him? For a third-order determinant, there is a heuristic (visual) triangle rule it looks like this:

The product of the elements of the main diagonal (from the upper left corner to the lower right) The product of the elements forming the first triangle "perpendicular" main diagonal The product of the elements forming the second triangle "perpendicular" main diagonal
The product of elements of the side diagonal (from the upper right angle to the lower left) The product of the elements forming the first triangle "perpendicular" by the side diagonal The product of the elements forming the second triangle "perpendicular" side diagonal
Then the determinant is equal to the difference of the values \u200b\u200bobtained in step and

If you write all these numbers, then we will get the following expression:

Nevertheless, remembering the method of calculation in this form is not necessary, it is enough in the head just to keep triangles and the idea itself, which is what it makes up and what is then deducted from something).

Let's illustrate the triangle method on the example:

1. Calculate the determinant:

Let's deal with what we fold, and what - we subtract:

The components that go with the "plus":

This is the main diagonal: the product of the elements is equal

The first triangle, "perpendicular main diagonal: the product of elements is equal

The second triangle, "perpendicular main diagonal: the product of the elements is equal

We fold three numbers:

The components that go with the "minus"

This is a side diagonal: the product of the elements is equal

The first triangle, "perpendicular to the side diagonal: the product of the elements is equal

The second triangle, "perpendicular to the side diagonal: the product of the elements is equal

We fold three numbers:

All that remains to do is to deduct from the sum of the terms "with a plus" amount of the terms "with a minus":

In this way,

As you can see, nothing complicated and supernatural in the calculation of the third order determinants is not. It is just important to remember about the triangles and not allow arithmetic errors. Now try to calculate yourself:

Check:

The first triangle, perpendicular main diagonal:
The second triangle, perpendicular main diagonal:
The amount of the terms with a plus:
The first triangle perpendicular to the side diagonal:
The second triangle, perpendicular to the side diagonal:
The amount of the terms with a minus:
The amount of components with a plus minus the amount of the terms with a minus:

Here is another couple of determinants, they calculated their meanings on their own and compare with the answers:

Answers:

Well, all the coincided? Great, then you can move on! If there are difficulties, then the Council is mine: there is a bunch of software for calculating the determinant online. All you need is to come up with your identifier, calculate it yourself, and then compare with what the program will consider. And so as long as the results do not start the coincidence. I'm sure this moment will not wait long to wait!

Now let's go back to the determinant who I wrote when he spoke about the equation of the plane passing through three setpoints:

All you need is to calculate its value directly (by the method of triangles) and equate the result to zero. Naturally, because - variables, then you will get some expression, depending on them. It is this expression that will be the equation of a plane passing through three set points that are not lying on one straight line!

Let's illustrate the above-mentioned example:

1. Construct the equation of the plane passing through points

We write the determinant for these three points:

Simplify:

Now we calculate it directly according to the rule of triangles:

\\ [(\\ left | (\\ begin (array) (* (20) (C)) (x + 3) & 2 & 6 \\\\ (y - 2) & 0 & 1 \\ (Z + 1) & 5 & 0 \\ END (Array)) \\ \\ CDOT 5 \\ CDOT 6 -) \\]

Thus, the equation of the plane passing through the points has the form:

Now try to solve one task on your own, and then we will discuss it:

2. Find the equation of the plane passing through the points

Well, let's now discuss the decision:

We make a determinant:

And calculate its value:

Then the equation of the plane is:

Or, shorting on, we get:

Now two tasks for self-control:

Construct the equation of the plane passing through three points:

Answers:

All coincided? Again, if there are certain difficulties, then my advice is: you take three points from my head (with a great degree of probability they will not lie on one straight), build a plane on them. And then check yourself online. For example, on the site:

However, with the help of determinants, we will build not only the equation of the plane. Remember, I told you that the vectors defined not only the scalar product. There is still a vector, as well as a mixed work. And if the scalar product of two vectors and there will be a number, then the vector product of two vectors and will be vector, and this vector will be perpendicular to the specified:

Moreover, its module will be equal to the area of \u200b\u200bthe parallelogram, which is preceded by vectors and. This vector will need to calculate the distance from the point to direct. How do we consider the vector product of vectors and, if their coordinates are set? The third order determinant comes to the rescue. However, before I proceed to the algorithm for calculating the vector art, I have to make a small lyrical retreat.

This retreat concerns basic vectors.

Schematically, they are depicted in the picture:

What do you think, why are they called basic? The fact is that :

Or in the picture:

The justice of this formula is obvious, because:

Vector art

Now I can proceed to the introduction of a vector work:

The vector product of two vectors is called the vector that is calculated by the following rule:

Now let's give a few examples of the vector art calculation:

Example 1: Find vector vectors:

Solution: I make up the determinant:

And calculate it:

Now from writing through basic vectors, I will return to the usual recording of the vector:

In this way:

Now try.

Ready? Check:

And traditionally two tasks for control:

Find vector clip art:
Find vector clip art:

Answers:

Mixed product of three vectors

The last design that will need me is a mixed product of three vectors. It, as well as scalar, is a number. There are two ways to calculate it. - Through the determinant, - through a mixed work.

Namely, let us have three versions:

Then the mixed product of three vectors, denoted by can be calculated as:

1. - That is, a mixed product is a scalar product of a vector on a vector product of two other vectors.

For example, a mixed product of three vectors is:

Independently try to calculate it through a vector product and make sure that the results will match!

And again - two examples for self solutions:

Answers:

Select the coordinate system

Well, now we have all the necessary foundation of knowledge to solve complex stereometric tasks on geometry. However, before proceeding directly to the examples and algorithms of their decision, I believe that it will be useful to stop still on what question: how exactly select the coordinate system for a particular figure. After all, it is the choice of the mutual location of the coordinate system and the figure in space will ultimately determine how cumbersome will be calculations.

I remind you that in this section we consider the following figures:

Rectangular parallelepiped
Direct prism (triangular, hexagonal ...)
Pyramid (triangular, quadrangular)
Tetrahedron (one and the same as the triangular pyramid)

For rectangular parallelepipeda or cube, I recommend that you build:

That is, I will put an "into the angle". Cube and parallelepiped are very good figures. For them, you can always easily find the coordinates of his vertices. For example, if (as shown in Figure)

the coordinates of the vertices are as follows:

To remember it, of course, no need to remember how it is better to have a cube or rectangular parallelepiped - preferably.

Direct prism

Prism is a more harmful figure. Its located in space can be different. However, I seem most acceptable to me:

Triangular Prism:

That is, one of the sides of the triangle we fully put on the axis, and one of the vertices coincides with the start of coordinates.

Hexagonal prism:

That is, one of the vertices coincides with the start of coordinates, and one of the parties lies on the axis.

Quadrangular and hexagonal pyramid:

Situation, similar to Cuba: Two sides of the base we combine with the coordinate axes, one of the vertices we combine with the beginning of the coordinates. The only minor complexity will calculate the coordinates of the point.

For hexagonal pyramid - similarly as for a hexagonal prism. The main task is again in the search for the coordinates of the vertex.

Tetrahedron (triangular pyramid)

The situation is very similar to the one that I led for a triangular prism: one peak coincides with the beginning of the coordinates, one side lies on the coordinate axis.

Well, now we are finally close to getting close to solving problems. From what I said at the very beginning of the article, you could make this conclusion: most C2 tasks are divided into 2 categories: challenges at the angle and tasks per distance. At first, we will consider the tasks of finding the angle. They, in turn, are divided into the following categories (as complexity increases):

Tasks for searching corners

Finding the angle between two straight
Finding the angle between two planes

Let's consider these tasks consistently: let's start by finding the angle between two straight. Well, remember, and did we decide with you similar examples before? I remember, because we had something like that ... We were looking for the angle between two vectors. I will remind you if two versions are given: and, the corner between them is from the ratio:

Now we have a goal - finding an angle between two straight. Let's turn to the "flat picture":

How much did the corners do with the intersection of two straight lines? Already pieces. The truth is not equal from them only two, others are vertical to them (and therefore they coincide with them). So what kind of angle should we be considered an angle between two straight: or? Here is a rule: the angle between two direct always no more than degrees. That is, from two angles, we will always choose an angle with the smallest degree. That is, in this picture, the angle between two straight is equal. To do not bother with a search for the smallest of two angles, sly mathematics offered to use the module. Thus, the angle between two direct is determined by the formula:

You, like a careful reader, had to arouse the question: And where, in fact, we will take these the most numbers that we need to calculate the cosine of the corner? Answer: We will take them from direct vectors! Thus, the algorithm for finding an angle between two straight lines is as follows:

We apply formula 1.

Or in more detail:

We are looking for coordinates of the guide vector of the first direct
We are looking for coordinates of the guide vector second direct
Calculate the module of their scalar product
Looking for the length of the first vector
Looking for the length of the second vector
Multiply the results of paragraph 4 on the results of paragraph 5
We divide the result of paragraph 3 on the result of clause 6. We get a cosine of the angle between direct
If this result allows accurately calculating the angle, we are looking for it
Otherwise we write through the arquosine

Well, now it's time to move to the tasks: the solution of the first two I will demonstrate in detail, I will introduce another decision in short form, and I will only give answers to the last two tasks, you should spend all the calculations to them.

Tasks:

1. In Pra-Ville-Nome Tet-Ra-Ed-Rea Nai di, the corner between you-co-Tet-Ra-ED-RA and the mea-di-bo-ko-coordinates.

2. In the Pra-Ville-Neu-coal Pi-Ra-Mi-de Stro-Ros, OS-Na-Viya are equal, and the bouquet of ribs are equal, Nay-di the corner between the straight and.

3. The lengths of all the ribs of Pra-Ville Che-you-Rah-Coal Pi-Ra-Mi are equal to each other. Nai-di the angle between the straighties and if from-re-zok - the co-alone given Pi-Ra-Mi-dwi, the point is se-re-di-on her bouquet rib

4. On the edge of the cube from-me-per point so that the nai-di the corner between the straight and

5. Point - se-re-di-on edges Cuba Nai-di the corner between straight and.

I misunderstood the tasks in this order. While you have not had time to start navigate in the coordinate method, I myself disassemble the most "problem" figures, and you will give you to deal with the simplest cube! Gradually, you have to learn to work with all the figures, the complexity of the tasks I will increase from the topic to the topic.

We proceed to solving problems:

1. Draw a tetrahedron, put it in the coordinate system as I designed earlier. Since the tetrahed is correct - then all its faces (including base) - the right triangles. Since we are not given the length of the side, then I can take it equal. I think you understand that the angle will not really depend on how our tetrahedron will "stretch"?. Also spend in Tetrahedra height and median. Along the way, I paint its base (it will also come in handy).

I need to find the angle between and. What do we know? We know only the point coordinate. So, it is necessary to find more coordinates of points. Now we think: the point is the point of intersection of heights (or bisetriss or median) of the triangle. And the point is a raised point. The point is the middle of the segment. Then we definitively need to find: the coordinates of the points :.

Let's start with the simplest: the coordinates of the point. Look at Figure: It is clear that the point of the point is zero (the point lies on the plane). Her ordinate is equal to (since - the median). It is harder to find it abscissa. However, it is easily done on the basis of the Pythagora theorem: Consider a triangle. Its hypotenuse is equal, and one of the cathets is equal then:

Finally we have :.

Now we find the coordinates of the point. It is clear that her appliquet is again zero, and its ordinate is the same as the point, that is. Find her abscissa. This is done trivially, if you remember that the heights of the equilateral triangle of the intersection point are divided in proportion, counting from the top. Since:, then the desired abscissa point equal to the length of the segment is equal to :. Thus, the coordinates of the point are equal:

Find the coordinates of the point. It is clear that its abscissa and ordinate coincide with the abscissa and the ordinary point. And the applicature is equal to the length of the segment. - This is one of the cathes of the triangle. Triangle hypotenuse is a cut - catat. He is looking for for reasons that I highlighted a bold:

The point is the middle of the segment. Then we need to remember the formula of the coordinates of the middle of the segment:

Well, all, now we can search the coordinates of the guide vectors:

Well, everything is ready: we substitute all the data in the formula:

In this way,

Answer:

You should not scare such "scary" answers: for the tasks C2 is common practice. I would rather surprised the "beautiful" answer in this part. Also, as you noted, I practically did not resort to anything, except for the Pythagoreo theorem and the property of the equilateral triangle heights. That is, to solve the stereometer task, I used the minimum of stereometry. The win in this partially "quenching" is quite bulky computing. But they are algorithm enough!

2. I will show the correct hexagonal pyramid along with the coordinate system, as well as its base:

We need to find the angle between straight and. Thus, our task is reduced to the search for the coordinates of the points :. The coordinates of the last three we will find on a small pattern, and we will find the coordinate of the vertices through the point coordinate. Works in bulk, but you need to start it!

a) The coordinate: it is clear that its applicatis and ordinate are equal to zero. We find the abscissa. To do this, consider a rectangular triangle. Alas, we are known only by hypotenuse, which is equal. Watch we will try to find (for it is clear that the doublest length of the category will give us an abscissue point). How do we look for her? Let's remember that for the figure we lie at the base of the pyramid? This is the right hexagon. What does it mean? This means that he has all the parties and all the corners are equal. It would be necessary to find one such angle. Any ideas? Ideas mass, but there is a formula:

The sum of the corners of the correct N-parliament is equal to .

Thus, the sum of the angles of the correct hexagon is equal to degrees. Then each of the corners is equal to:

We look at the picture again. It is clear that the cut - bisector angle. Then the angle is equal to degrees. Then:

Then, from where.

Thus, has coordinates

b) Now you can easily find the point coordinate :.

c) We will find the coordinates of the point. Since its abscissa coincides with the length of the segment, it is equal to. It is not very difficult to find the ordinate: if we connect the points and a point of intersection of direct designation, let's say for. (Make a simple construction itself). Then thus, the ordinate point B is equal to the sum of the lengths of the segments. Re-turn to the triangle. Then

Then because then the point has coordinates

d) Now we will find the coordinates of the point. Consider a rectangle and prove that thus point coordinates:

e) It remains to find the coordinates of the vertices. It is clear that its abscissa and ordinate coincides with the abscissa and the ordinary point. We find the applicant. Since, then. Consider a rectangular triangle. By the condition of the problem, the lateral edge. This is the hypotenus of my triangle. Then the height of the pyramid - catat.

Then the point has coordinates:

Well, everything, I have the coordinates of all points of interest to me. I am looking for coordinates of direct vectors of direct:

We are looking for an angle between these vectors:

Answer:

Again, when solving this task, I did not use any irregular techniques, except for the formula of the amount of the corners of the correct N-square, as well as the definition of cosine and the sine of the rectangular triangle.

3. Since we again are not given the length of the ribs in the pyramid, then I will consider them equal to one. Thus, since all ribs, not just side, are equal to each other, then at the base of the pyramid and the square is lying, and the side faces are the right triangles. We will show this pyramid, as well as its base on the plane, noting all the data given in the text of the task:

We are looking for the angle between and. I will make very short calculations when I search for the coordinates of points. You will need to "decipher" them:

b) - the middle of the segment. Its coordinates:

c) Cut length I will find on the Pythagora theorem in the triangle. I will find on the Pythagorean theorem in the triangle.

Coordinates:

d) - midt of segment. Its coordinates are equal

e) vector coordinates

f) vector coordinates

g) We are looking for an angle:

Cube is the simplest figure. I am sure that you will deal with her yourself. Answers to tasks 4 and 5 are as follows:

Finding the angle between the straight and plane

Well, the time of simple tasks is over! Now the examples will be even more difficult. To find the corner between the straight and plane, we will be as follows:

By three points we build a plane equation
,
Using third-order determinant.
By two points we are looking for a direct guide coordinates:
We use the formula for calculating the angle between the straight and plane:

As you can see, this formula is very similar to the fact that we used to search for corners between two straight. The structure of the right part is simply the same, and we are now looking for sinus now, and not cosine, as before. Well, one opposite action was added - searching the equation of the plane.

Let's not postpone in a long box solution of examples:

1. Os-no-va-ni-it is a straight procure-lap-ben-smta Raughty-na-de-re-coal nickname you-so-one prize is equal. Nay-di the corner between straight and flat-co-st

2. In the direct-Mo-Mr. Pa-Ral-les-Le-Pi-de-Die from the Nay-di-level corner between straight and flat-co -

3. In Pra-Ville, the neck-coal prize-alto all ribs are equal. Nai-di the corner between straight and flat-co-st.

4. In Pra-Ville Tre-Coal Pi-Ra-Mi-de with Os-no-Va Ni-West-Na-Di-Thief, Obra-Zo-Wan a flat-co-co-copy of Os-no-va and straight, pro-ho-son through the re-di ribs and

5. The lengths of all the ribs of pra-vil-ote four-born Pi-Ra-Mi-dy are equal to each other. Nay-di the angle between straight and flat-co-stew if the point is Ce-re-di-on-co-co-rib Pi-Ra-Mi-dy.

Again, I will decide the first two tasks in detail, the third - briefly, and the last two leave you for an independent decision. In addition, you have already had to deal with triangular and quadrangular pyramids, but with prisms - so far there are no.

Solutions:

1. Show a prism as well as its base. It is compatible with the coordinate system and note all the data that is given in the Terk Condition:

I apologize for some non-compliance with the proportions, but to solve the problem, it is essentially not so important. The plane is simply the "rear wall" of my prism. It is enough just to guess that the equation of such a plane is:

However, it can be shown directly:

Choose arbitrary three points on this plane: for example,.

Make a plane equation:

Exercise to you: independently calculate this determinant. Did you succeed? Then the equation of the plane is:

Or simply

In this way,

To solve the example, I need to find the coordinates of the guide vector straight. Since the point has fallen with the beginning of coordinates, the vector coordinates simply coincide with the coordinates of the point for this we will find at the beginning of the coordinates of the point.

To do this, consider a triangle. We will spend the height (it is median and bisector) from the top. Since, the ordinate point is equal. In order to find the abscissa of this point, we need to calculate the length of the segment. According to Pythagora theorem, we have:

Then the point has coordinates:

The point is "raised" to the point:

Then the coordinates of the vector:

Answer:

As you can see, there is nothing fundamentally difficult in solving such tasks. In fact, the process further simplifies "straight" such a figure as Prism. Now let's move on to the following example:

2. Draw a parallelepiped, we carry out a plane and direct, as well as separately draw its lower base:

First we find the plane equation: the coordinates of the three points lying in it:

(The first two coordinates are obtained by an obvious way, and the last coordinate you can easily find pictures from the point). Then constitute the equation of the plane:

Calculate:

We are looking for the coordinates of the guide vector: it is clear that its coordinates coincide with the coordinates of the point, is not it? How to find coordinates? This is the coordinates of the point raised along the appliquet axis per unit! . Then look for the desired angle:

Answer:

3. Put the correct hexagonal pyramid, and then spend the plane and direct.

There is even a plane to draw a problem, not to mention the solution of this task, however, the coordinate method is still! It is in his versatility and is its main advantage!

The plane passes through three points :. We are looking for their coordinates:

one) . Himself output coordinates for the last two points. You will be useful for this solution to the challenge with a hexagonal pyramid!

2) we build the equation of the plane:

We are looking for the coordinates of the vector :. (see the task with a triangular pyramid again!)

3) We are looking for an angle:

Answer:

As you can see, nothing is supernatural in these tasks. It is only necessary to be very careful with roots. To the last two tasks I will give only answers:

How could you make sure the technique of solving tasks everywhere the same: the main task to find the coordinates of the vertices and substitute them into certain formulas. We left to consider another class of challenges for calculating the corners, namely:

Calculation of angles between two planes

The algorithm solutions will be:

For three points we are looking for the equation of the first plane:
For other three points we are looking for the equation of the second plane:
We use the formula:

As you can see, the formula is very similar to the previous two, with which we searched the corners between straight and between the straight and plane. So remember this you will not be much difficulty. We immediately go to the analysis of tasks:

1. ST-RO-OS-NO-VIL-VIL-VILTER TRE-CONSIDE CONSUITE WHERE, and DI-HALL BO-KO-CO-COP is equal. Nay-di the angle between the F-Co-Stew and the F-Co-Stew Os-no-Viya prize-we.

2. In Pra-Ville-Mi-Deh-Coal Pi-Ra-Mi-de, all ribs are equal, the sinus of the corner between the F-Co-Stew and Co-Stew, Pro-Ho-Fith through the Pen-Pen-Di-Liar Pen-Di-Liar, but straight.

3. In the correct che-the-coal-coal prize of ST-Ro-us, Os-Na-Via is equal, and the bouquet of edges are equal. On the edge of from-me - to the point so that. Find the angle between the flat-ko-mi and

4. In the Pra-Willian four-born prize-ours, the OS-NA-VIA is equal, and the bou--way Ribra is equal. On the edge of from-me-a point so that the nai-di the corner between the flat-ko-mi and.

5. In Cuba, the Nau-Di Ko-Si-Nus angle between the flat-co-stey and

Tasks solutions:

1. Rise the correct (at the base is an equilateral triangle) a triangular prism and note on it planes that appear in the condition of the problem:

We need to find the equations of two planes: the base equation is obtained trivial: you can make an appropriate determinant for three points, I will constitute the equation immediately:

Now we will find the point equation has the coordinates of the point - as it is the median and the height of the triangle, it is easily located on the Pythagora theorem in the triangle. Then the point has coordinates: find the application point for this Consider a rectangular triangle

Then we obtain these coordinates: we will compose the equation of the plane.

Calculate the angle between the planes:

Answer:

2. Make drawing:

The most difficult thing is to understand that this is such a mysterious plane passing through the point perpendicularly. Well, the main thing is that? The main thing is attentiveness! In fact, direct is perpendicular. Straight is also perpendicular. Then the plane passing through these two straight lines will be perpendicular to the straight, and, by the way, pass through the point. This plane also passes through the top of the pyramid. Then the desired plane - and the plane is already given to us. We are looking for the coordinates of the points.

The coordinate of the point will find through the point. From a small drawing it is easy to remove that the coordinates of the point will be like that: what is left now to find to find the coordinates of the peak of the pyramid? You still need to calculate its height. This is done with the help of the same Pythagore's theorem: first prove that (trivially of small triangles, forming a square at the base). Since under the condition, we have:

Now everything is ready: the coordinates of the vertices:

Make a plane equation:

You are already special in the calculation of the determinants. Without difficult, you will get:

Or otherwise (if there are both parts for the root of two)

Now we find the equation of the plane:

(You didn't forget how we get the equation of the plane, however? If you do not understand where this minus one came from, then come back to the definition of the equation of the plane! Just always before that it turned out that my plane belonged to the beginning of the coordinates!)

Calculate the determinant:

(You can notice that the equation of the plane coincided with the equation of direct passing through the points and! Think why!)

Now we calculate the angle:

We also need to find sinus:

Answer:

3. Caverny question: What is a rectangular prism, what do you think? This is just a particularly well-known parallelepiped! Immediately do the drawing! You can even separately do not depict the basis, the benefits of it here is a bit here:

The plane, as we have already noticed before, is written in the form of equation:

Now make a plane

The equation is the equation of the plane:

We are looking for an angle:

Now answers to the last two tasks:

Well, now it's time to rest a little, because we are great and you have done a huge job!

Coordinates and vectors. Advanced level

In this article we will discuss with you another class of tasks that can be solved using the coordinate method: tasks for calculating the distance. Namely, we will consider the following cases:

Calculating the distance between cross-country straight.

I ordered these tasks as their complexity increases. Most just turns out to find distance from point to planeAnd the most difficult thing is to find distance between cross-country straight. Although, of course, there is nothing impossible! Let's not postpone in a long box and immediately proceed to consider the first class of tasks:

Calculating the distance from the point to the plane

What do we need to solve this task?

1. The coordinates of the point

So, as soon as we get all the necessary data, we use the formula:

As we build the equation of the plane you should already be known from the previous tasks that I understood in the last part. Let's immediately proceed to tasks. The scheme is as follows: 1, 2 - I help you to decide, and quite detail, 3, 4 - Only the answer, the decision you spend and compare. Started!

Tasks:

1. Dan Cube. Cube's edge length is equal. Nai di-Thief from Ce-di-di from-cut to flat-co-st

2. Dana Pra-Vil-Naya Che-Mi-Ya-Coal-Naya Pi-Mi-da Boe-co-co-rib Stro-Ro-on Os-No-Via is equal. NAY-DI-THAT STO-YAST from the point to the flat-co-comma where - se-re-di-on ribs.

3. In Pra-Ville Tre-Coal Pi-Ra-Mi-de with Os-No-Va-Ni-Ko-Co-Way Equally, and a hundred-ro-on Os-na- equal to. Nai di-Thief from the Ver-Shi-we to flat-co-st.

4. In the Pra-Ville seam-coal prize-alone, all Ribra is equal. NAY-DI-THAT STO-YAST from point to flat-co-st.

Solutions:

1. Draw a cube with single edges, we build a segment and a plane, the middle of the segment we denote the letter

At first, let's start with the lung: find the coordinates of the point. Since that (remember the coordinates of the middle of the segment!)

Now we compile the equation of the three-point plane

\\ [\\ left | (\\ Begin (Array) (* (20) (C)) X & 0 & 1 \\\\ Y & 1 & 0 \\\\ Z & 1 & 1 \\ END (Array)) \\ Right | \u003d 0 \\]

Now I can proceed to the search for the distance:

2. We begin again from the drawing, where we celebrate all the data!

For the pyramid it would be useful separately to draw its base.

Even the fact that I paint as a chicken paw does not prevent us with ease to solve this task!

Now it's easy to find the point coordinates

As the coordinates of the point, then

2. Since the coordinates of the point A - the middle of the segment, then

We also find the coordinates of two more points on the plane to make the equation of the plane and simplify it:

\\ [\\ left | (\\ Left | (\\ Begin (Array) (* (20) (C)) X & 1 & (\\ FRAC (3) (2)) \\\\ Y & 0 & (\\ FRAC (3) (2)) \\\\ Z & 0 & (\\ FRAC ( (\\ SQRT 3)) (2)) \\ END (Array)) \\ Right |) \\ RIGHT | \u003d 0 \\]

Since the point has coordinates:, then we calculate the distance:

Answer (very rare!):

Well, figured out? It seems to me that everything is also technically as in those examples that we considered with you in the previous part. So I am sure that if you have mastered the material, then you will not be difficult to solve the remaining two tasks. I will only give answers:

Calculation of distance from direct to the plane

In fact, there is nothing new here. How can the straight and plane relative to each other can be located? They have all the possibilities: cross, or directly parallel to the plane. What do you think, the equal distance from a straight line to the plane with which this direct intersects? It seems to me that it is clear that the distance is zero. Uninteresting case.

The second case is cunning: the distance is already nonzero. However, since the straight parallel plane, then each point is equivalent to this plane:

In this way:

This means that my task was drilled to the previous one: we are looking for the coordinates of any point on a straight line, we look for the equation of the plane, calculate the distance from the point to the plane. In fact, such tasks in the exam are extremely rare. I managed to find only one task, and the data in it were such that the coordinate method was not very applied to it!

We now turn to another, a much more important class of tasks:

Calculation of the distance point to direct

What do we need?

1. The coordinates of the point from which we are looking for the distance:

2. Coordinates of any point lying on the line

3. Direct vectors direct coordinates

What formula?

What does the denominator of this fraction mean to you and so it should be clear: it is the length of the guide vector straight. Here is a very cunning numerator! The expression means the module (length) of the vector product of vectors and how to calculate the vector work, we were studied in the previous part of the work. Update your knowledge, they will now be very useful to us!

Thus, the problem solving algorithm will be the following:

1. We are looking for the coordinates of the point from which we are looking for the distance:

2. We are looking for the coordinates of any point on the line, which we are looking for the distance:

3. Build vector

4. Build the line guide vector

5. Calculate vector art

6. We are looking for the length of the resulting vector:

7. Calculate the distance:

We have a lot of work, and examples will be quite complicated! So now focus all the attention!

1. Dana Pra-Vil-Naya Tre-Coal-Naya Pi-Ra-Mi-yes with Ver-Shih. One-Ro-on Os-no-Viya Pi-Ra-Mi-dya is equal, you-so-so is equal. Nai di-Thief from the se d-di-ko-co-rib to straight, where the points and - the re-di ribs and co-from- VET-DOWN.

2. The lengths of the ribs and the direct-m-coal-but-goa Parale-le-le-pi-yes are equal to co-from-vessels - but also the NAI-Di-Thief from Ver-Shi-re-direct

3. In the Pra-Ville seam-coal prize-alone, all ribs are equal to the NAI-Di-Thief Route from point to straight

Solutions:

1. Make a neat drawing, which mark all the data:

We have a lot of work with you! I would first like to describe the words that we will look for and in what order:

1. The coordinates of the points and

2. Coordinates of the point

3. The coordinates of the points and

4. The coordinates of vectors and

5. Their vector art

6. Vector length

7. Vector length length

8. Distance from to

Well, we have a lot of work! We are accepted for her, drossing the sleeves!

1. To find the coordinates of the pyramid height, we need to know the coordinates of the point of its applicature equal to zero, and the ordinate is equal to the abscissa of it is equal to the length of the segment since the height of the equilateral triangle, then it is divided into relationship, counting from the top, hence. Finally, they received coordinates:

Coordinates Points

2. - Middle Cut

3. - Mid Segment

Mid-cut

4.Copinates

Coordinates of the vector

5. Calculate vector art:

6. The length of the vector: the easiest way is to replace that the segment is the middle line of the triangle, which means it is equal to half the base. So that.

7. We consider the length of the vector work:

8. Finally, we find the distance:

UV, well! Honestly, I will say: the solution to this problem with traditional methods (through construction) would be much faster. But here I all reduced to the finished algorithm! So I think that the algorithm is clear to you? Therefore, I will ask you to solve the remaining two tasks yourself. Compare answers?

Again, I repeat: these tasks are easier (faster) to solve through the constructions, and not resorting to the coordinate method. I demonstrated such a solution to the decision only to show you a universal method that allows you to hold anything. "

Finally, consider the last class of tasks:

Calculating the distance between cross-country straight

Here, the algorithm for solving tasks will be similar to the previous one. What we have:

3. Any vector connecting points first and second straight:

How are we looking for the distance between straight?

The formula is as follows:

The numerator is a module of a mixed product (we were administered in the previous part), and the denominator is as in the previous formula (module of the vector product of the direct vectors of direct, the distance between which we are looking for).

I will remind you that

then the formula for the distance can be rewritten in the form:

Single determinant to share the determinant! Although, to be honest, I'm not at all joking here! This formula, in fact, is very cumbersome and leads to sufficiently complex calculations. In your place, I would resort to it only in the most extreme case!

Let's try to solve several tasks using the method outlined above:

1. In Pra-Ville, the Tre-Coal Prize, all Ribr Ko-Roy are equal, the Nai di-Those Rouner of the straight and.

2. Dana-Vil-Naya Tre-Coal-Naya Prize-Ma All Rib Os-no-Via-Way is equal to se-human, pro-Ho-grandfather through the Bo-Co-Woe The edge and se-re-di is the ribs of Java-Lhaa-Xia Kvad-Ra-Tom. NAY-DI-THES ROSTOZHONE BETWEEN RIATS AND

I solve the first, and relying on it, you decide the second!

1. I draw a prism and mark straight and

The coordinates of the point C: then

Coordinates Points

Coordinates of the vector

Coordinates Points

Coordinates of the vector

\\ [\\ left ((B, \\ Overrightarrow (A (A_1)) \\ Overrightarrow (B (B_1))) \\ Right) \u003d \\ left | (\\ Begin (Array) (* (20) (L)) (\\ Begin (Array) (* (20) (C)) 0 & 1 & 0 End (Array)) \\\\ (\\ Begin (Array) (* (20) (C)) 0 & 0 & 1 \\ END (Array)) \\\\ (\\ Begin (Array) (* (20) (C)) (\\ FRAC ((\\ SQRT 3)) (2)) & (- \\ FRAC (1) (2)) & 1 \\ End (Array)) \\ END (Array)) \\ RIGHT | \u003d \\ FRAC ((\\ SQRT 3)) (2) \\]

We consider vector product between vectors and

\\ [\\ Overrightarrow (A (A_1)) \\ CDOT \\ OVERRIGHTARROW (B (C_1)) \u003d \\ left | \\ Begin (Array) (L) \\ Begin (Array) (* (20) (C)) (\\ Overrightarrow i) & (\\ Overrightarrow J) & (\\ Overrightarrow K) \\ END (Array) \\\\\\ Begin (Array ) (* (20) (C)) 0 & 0 & 1 \\ END (Array) \\\\\\ Begin (Array) (* (20) (C)) (\\ FRAC ((\\ SQRT 3)) (2)) & (- \\ - \\ FRAC ((\\ SQRT 3)) (2) \\ Overrightarrow K + \\ FRAC (1) (2) \\ Overrightarrow i \\]

Now we consider it a length:

Answer:

Now try to accurately fulfill the second task. The answer to it will be :.

Coordinates and vectors. Brief description and basic formulas

Vector - directional cut. - Beginning of vector, - Content vector.
The vector is denoted or.

Absolute valuevector - Cut length depicting vector. Referred to as.

Coordinates of the vector:

,
where - the ends of the vector \\ displaystyle a.

Sum of vectors :.

Making vectors:

Scalar product of vectors:

The scalar product of vectors is equal to the product of their absolute values \u200b\u200bon the cosine of the angle between them:

Become a student YouClever,

Prepare for OGE or EGE in mathematics,

And also access YouClever's textbook without restrictions ...

Before you learn all about the vectors and operations on them, tune in to solving an easy task. There are vector of your enforcement and vector of your innovative abilities. The vector of enterprise leads you to goal 1, and the vector of innovative abilities - to the goal 2. The rules of the game are such that you cannot move immediately in the directions of these two vectors and reach two goals at once. Vectors interact, or, if we say a mathematical language, some operations are performed above the vectors. The result of this operation becomes the result "result", which leads you to goal 3.

And now tell me: What operation on the vectors "enterprise" and "innovative abilities" is the "result" vector? If you can not say right away, do not lose. As you study this lesson, you can answer this question.

As we have already seen above, the vector necessarily goes from some point A. For straight to some point B.. Consequently, each vector has not only a numeric value - length, but also physical and geometric - orientation. From this output the first, the simplest determination of the vector. So, the vector is a directed section coming from the point. A. To point B.. It is referred to.

And to proceed to different operations with vectors We need to get acquainted with another vector definition.

The vector is the type of point presentation to which you want to get from some starting point. For example, a three-dimensional vector is usually written in the form (x, y, z) . Talking quite simply, these numbers mean how far needs to go through three different directions to get to the point.

Let vector be given. Wherein x. = 3 (right hand points to the right) y. = 1 (Left hand points forward), z. = 5 (under the point there is a staircase leading up). According to this data, you will find a point by passing 3 meters in the direction indicated by the right hand, then 1 meter in the direction indicated by your left hand, and then the staircase is waiting for you and, rising by 5 meters, you will finally find yourself at the end point.

All other terms are clarifications of the explanation presented above, necessary for various operations over vectors, that is, solutions to practical problems. Let's go through these more stringent definitions, stopping on typical tasks on the vectors.

Physical examples Vector magnitudes can be a displacement of the material point moving in space, speed and acceleration of this point, as well as the force acting on it.

Geometric vector presented in a two-dimensional and three-dimensional space in the form directed cut. This is a segment that distinguishes the beginning and the end.

If a A. - the beginning of the vector, and B. - Its end, then the vector is indicated by a symbol or one lowercase letter. In the figure, the end of the vector is indicated by the arrow (Fig. 1)

Lena (or module) Geometric vector is called the length of the segment generating it

Two vectors are called equal if they can be combined (with the coincidence of directions) by parallel transfer, i.e. If they are parallel, directed in the same side and have equal lengths.

Physics are often considered fastened vectors, specified point of application, long and direction. If the vector application point does not matter, it can be transferred, retaining the length and direction to any point of space. In this case, the vector is called free. We will agree to consider only loose vectors.

Linear operations on geometric vectors

Multiplication of vector by number

Work vector number The vector is called the vector from the vector with a stretch (with) or compression (at) per time, and the direction of the vector is preserved if, and changes to the opposite if. (Fig. 2)

From the definition it follows that vectors and \u003d are always located on one or on parallel straight lines. Such vectors are called collinear. (It can also be said that these vectors are parallel, however, in the vector algebra, it is customary to say "collinear".) Fairly and reverse statement: if vectors and collinear, then they are associated with the attitude

Consequently, equality (1) expresses the condition of the collinearity of two vectors.

Addition and subtraction of vectors

When adding vectors you need to know that sum The vectors are called the vector, the beginning of which coincides with the beginning of the vector, and the end - with the end of the vector, provided that the beginning of the vector is applied to the end of the vector. (Fig. 3)

This definition can be distributed to any finite number of vectors. Let in space given n. free vectors. When adding several vectors for their sum, the closing vector is taken, the beginning of which coincides with the beginning of the first vector, and the end - with the end of the last vector. That is, if the end of the vector is to attach the beginning of the vector, and by the end of the vector - the beginning of the vector, etc. And finally, by the end of the vector - the beginning of the vector, the sum of these vectors is the closing vector , whose start coincides with the beginning of the first vector, and the end - with the end of the last vector. (Fig. 4)

The components are called the components of the vector, and the formulated rule - rule polygon. This polygon may not be flat.

When multiplying the vector to the number -1, the opposite vector is obtained. Vectors and have the same lengths and opposite directions. Their amount gives nuclear vector, whose length is zero. The direction of the zero vector is not defined.

In vector algebra there is no need to consider separate subtraction operation: the vector of the vector means add to the vector opposite vector, i.e.

Example 1. Simplify the expression:

that is, vectors can be folded and multiplied by numbers as well as polynomials (in particular, also tasks for simplifying expressions). Usually the need to simplify linearly similar expressions with vectors arise before calculating the works of vectors.

Example 2. Vectors and serve as diagonals ABCD parallelogram (Fig. 4a). Express via and vectors, and, which are the parties of this parallelogram.

Decision. Point of intersection of diagonals The parallelogram divides each diagonal in half. The lengths of the vectors required in the condition of the vectors are found either as half of the sums of vectors forming with the desired triangle, or as half of the differences (depending on the direction of the vector serving a diagonal), or, as in the latter case, half the amount taken with the minus sign. The result - vectors required in the condition:

There is every reason to believe that now you correctly answered the question about the "enterprise" and "innovative abilities" vector at the beginning of this lesson. The correct answer: Above these vectors is made of addition.

Solve tasks for vectors yourself, and then see solutions

How to find the length of the sum of the vectors?

This task occupies a special place in operations with vectors, as it involves the use of trigonometric properties. Suppose you got the task like next:

Danged vector vectors And the length of these vectors. Find the length of the difference between these vectors.

Solutions to this and other similar tasks and explanations, how to solve them - in the lesson " Addition of vectors: length of the sum of the vectors and the cosine theorem ".

And you can check the solution of such tasks on Calculator online "Unknown side of a triangle (addition of vectors and cosine theorems)" .

And where are the works of vectors?

The vector works on the vector are not linear operations and are considered separately. And we have lessons "scalar product of vectors" and "vector and mixed vectors".

Vector projection on the axis

The design of the vector on the axis is equal to the product of the length of the designed vector on the cosine of the angle between the vector and the axis:

As you know, projection point A. A direct (plane) is the base of the perpendicular, lowered from this point to the straight line (plane).

Let - arbitrary vector (Fig. 5), a and - projections of its start (point A.) and the end (points B.) on the axis l.. (To build a point projection A.) spend directly through the point A. Plane perpendicular to the line. The intersection of the direct and plane will determine the desired projection.

Component vector on the axis L. This vector lying on this axis is called, the beginning of which coincides with the projection of the beginning, and the end - with the projection of the end of the vector.

Projection of vector on the axis l. The number is called

equal to the length of the component vector on this axis, taken with a plus sign, if the direction of the component coincides with the direction of the axis l., and with a minus sign, if these directions are opposite.

The main properties of vector projections on the axis:

1. Projections of equal vectors on the same axis are equal to each other.

2. When multiplying the vector, its projection is multiplied by the same number.

3. Projection of the sum of vectors on any axis is equal to the amount of projections on the same axis of the components of the vectors.

4. The design of the vector on the axis is equal to the product of the length of the designed vector on the cosine of the angle between the vector and the axis:

Decision. We design vectors on the axis l. As defined in theoretical reference above. Fig. 5a Obviously, the projection of the vectors is equal to the amount of vectors projections. Calculate these projections:

We find the final projection of the sum of the vectors:

Vector connection with a rectangular Cartesian coordinate system in space

Acquaintance S. the rectangular Cartesian coordinate system in space took place in the appropriate lesson It is advisable to open it in a new window.

In an ordered coordinate axes system 0xyz. axis OX. called axis of abscissa, axis 0Y. – axian ordinate, and axis 0z. – axis of Applikat.

With an arbitrary point M. Space tie vector

called radius vectorpoints M.and spread it to each of the coordinate axes. Denote the values \u200b\u200bof the relevant projections:

Numbers x, Y, Zcalled coordinates of the point M., respectively abscissa, ordate and applikata, and recorded in the form of an ordered point of numbers: M (x; y; z) (Fig. 6).

The vector of a single length, the direction of which coincides with the axis direction, is called single vector(or orta) Axis. Denote by

Accordingly the orts of coordinate axes OX., Oy., Oz.

Theorem. Any vector can be decomposed on the orthop of the coordinate axes:

(2)

Equality (2) is called the decomposition of the vector according to the coordinate axes. The coefficients of this decomposition are the projections of the vector on the coordinate axes. Thus, the decomposition coefficients (2) on the coordinate axes are the coordinates of the vector.

After selecting in the space of a specific coordinate system, the vector and three of its coordinates uniquely define each other, so the vector can be recorded in the form

Representations of the vector in the form (2) and (3) are identical.

Collinear condition of vectors in coordinates

As we have noted, the vectors are called collinear if they are associated with the attitude

Let the vectors be given . These collinear vectors, if the coordinates of the vectors are associated with the attitude

that is, the coordinates of the vectors are proportional.

Example 6. Vectors are given . Are these vectors collinear?

Decision. Find out the ratio of the data coordinates of the vectors:

The coordinates of the vectors are proportional, therefore, the collinear vectors, or that the same is parallel.

Vector length and cosine guides

Due to the mutual perpendicularity of the coordinate axes of the vector length

equal to the length of the diagonal of a rectangular parallelepiped, built in vectors

and expressed equality

(4)

The vector is fully determined by the task of two points (beginning and end), so the coordinates of the vector can be expressed through the coordinates of these points.

Suppose in the specified coordinate system the beginning of the vector is at the point

and the end is at the point

From equality

Follows that

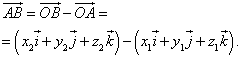
or in coordinate form

Hence, the coordinates of the vector are equal to the differences of the same end coordinates and the beginning of the vector . Formula (4) in this case will take the form

Vector direction define guides cosinees . These are cosine angles that the vector forms with axes OX., Oy. and Oz.. Denote these angles, respectively α , β and γ . Then the cosines of these corners can be found by formulas

Vector cosine guides are also the coordinates of the ort of this vector and, thus, the ort of the vector

Considering that the length of the ort of the vector is equal to one unit, that is

we obtain the following equality for cosine guides:

Example 7.Find vector length x. = (3; 0; 4).

Decision. Vector length is equal

Example 8.Points:

Find out whether the triangle is a chaired triangle, built at these points.

Decision. According to the length formula of the vector (6), we will find the length of the parties and install whether there are two equal among them:

Two equal parties were found, therefore, the need to look for the length of the third party disappears, and a given triangle is an equally chaired.

Example 9. Find the length of the vector and its guide cosines, if .

Decision. The coordinates of the vector are given:

Vector length is equal to square root from the sum of the squares of the coordinate vector:

We find guide cosines:

Solve the task on the vectors yourself, and then see the decision

Operations on vectors specified in coordinate form

Let two vectors and given by their projections:

We indicate actions on these vectors.

1. Subject:

or that the same

(With the addition of two vectors, the same coordinates are folded).

Such a concept as a vector is considered in almost all natural sciences, and it can have a completely different meaning, so it is impossible to give an unambiguous definition of the vector for all regions. But let's try to figure it out. So, vector - what is?

Concept of vector in classical geometry

The vector in geometry is a segment for which it is indicated which of its points is the beginning, and which is the end. That is, speaking easier, the vector is called a directional cut.

Accordingly, the vector is indicated (which is considered above), as well as a segment, that is, by two capital letters of the Latin alphabet with the addition of the line or arrow directed to the right. It can also be signed by a lowercase (small) letter of the Latin alphabet with a feature or arrow. The arrow is always directed to the right and does not change depending on the location of the vector.

Thus, the vector has a direction and length.

In the designation of the vector contains its direction. It is expressed as in the figure below.

The change in the direction changes the value of the vector to the opposite.

The length of the vector is called the length of the segment from which it is formed. It is indicated as a module from the vector. This is shown in the figure below.

Accordingly, zero is the vector, the length of which is zero. It follows from this that the zero vector is a point, and the points of the beginning and end coincide.

Vector length - the magnitude is always not negative. In other words, if there is a segment, it necessarily has some length or is a point, then its length is zero.

The very concept of point is basic and definition has no.

Addition of vectors

There are special formulas and rules for vectors with which you can perform addition.

Triangle rule. For the addition of vectors on this rule, it is sufficient to combine the end of the first vector and started the second, using the parallel transfer, and connect them. The resulting third vector and will be equal to the addition of the other two.

Rule parallelogram. To add on this rule, it is necessary to carry out both vector from one point, and then spend another vector from the end of each of them. That is, from the first vector will be held second, and from the second one. As a result, a new intersection point will be obtained and a parallelogram is formed. If you combine the intersection point of the beginning and the ends of the vectors, the resulting vector and will result in addition.

Through it is possible to perform and subtract.

Vector difference

Similar to the addition of vectors it is possible to accomplish their subtraction. It is based on the principle indicated in the figure below.

That is, the subtracted vector is enough to imagine in the form of a vector, to him the opposite, and make calculation according to the principles of addition.

Also, absolutely any nonzero vector can be multiplied by any number k, it will change its length in K times.

In addition to these, there are other formulas for vectors (for example, to express the length of the vector through its coordinates).

Location vectors

Surely many came across such a concept as a collinear vector. What is collinearity?

Collinearity vectors - equivalent parallelism direct. If two vectors lie on direct, which are parallel to each other, or on one straight line, then such vectors are called collinear.

Direction. Regarding each other, collinear vectors can be coated or oppositely directed, this is determined by the direction of vectors. Accordingly, if the vector is co-directed with another, then the vector, the opposite one, is oppositely directed.

The first figure shows two oppositely directed vector and the third, which is not collinear them.

After the introduction of the above properties, it is possible to define and equal to vectors are vectors that are directed in one direction and have the same length of the segments from which they are formed.

In many sciences, the concept of radius-vector is also applied. A similar vector describes the position of one point of the plane relative to another fixed point (often the origin of the coordinates).

Vectors in physics

Suppose, in solving the problem, a condition arose: the body moves at a speed of 3 m / s. This means that the body moves with a specific direction on one straight line, so this variable will be the magnitude of the vector. To solve, it is important to know and value, and direction, since, depending on the consideration, the speed can be equal to 3 m / c, and -3 m / s.

In general, the vector in physics is used to indicate the direction of force acting on the body and to determine the resultant.

When specifying these forces in the figure, they are denoted by arrows with the signed vector above it. Classically the length of the arrows is just as important, with the help of it indicate which force acts stronger, but this property is not worth relying on it.

Vector in linear algebra and mathematical analysis

The elements of linear spaces are also called vectors, but in this case they represent an ordered system of numbers describing some of the elements. Therefore, the direction in this case has no importance. The definition of the vector in classical geometry and in mathematical analysis is greatly different.

Projecting vectors

Spriesed vector - what is?

Quite often, for the correct and convenient calculation, it is necessary to decompose the vector located in two-dimensional or three-dimensional space, along the coordinate axes. This operation is necessary, for example, in mechanics when calculating the forces acting on the body. The vector in physics is used quite often.

To perform the projection, it is sufficient to lower the perpendicular from the beginning and end of the vector to each of the coordinate axes obtained on them segments and will be called the vector projection on the axis.

To calculate the length of the projection, it is sufficient to multiply its initial length to a certain trigonometric function, which is obtained by solving the mini-task. In fact, there is a rectangular triangle, in which hypotenuse is the source vector, one of the cathets - the projection, and the other catat is lowered by the perpendicular.

Vector concept. Free vector

Actions with vectors. Collinearity vectors

The rule of the addition of vectors according to the rule of triangles

What vectors are equal?

The coordinates of the vector on the plane and in space

The simplest tasks of analytical geometry.Actions with vectors in coordinates

How to find a vector on two points?

How to find a length of a segment?

How to find the length of the vector?

Coordinates and vectors. Middle roving

The equation of the plane passing through three setpoints

Vector art

Mixed product of three vectors

Select the coordinate system

Direct prism

Triangular Prism:

Hexagonal prism:

Quadrangular and hexagonal pyramid:

Tetrahedron (triangular pyramid)

Finding the angle between the straight and plane

Calculation of angles between two planes

Coordinates and vectors. Advanced level

Calculating the distance from the point to the plane

Calculation of distance from direct to the plane

Calculation of the distance point to direct

Calculating the distance between cross-country straight

Coordinates and vectors. Brief description and basic formulas

Linear operations on geometric vectors

Multiplication of vector by number

Addition and subtraction of vectors

Solve tasks for vectors yourself, and then see solutions

Vector projection on the axis

The main properties of vector projections on the axis:

Vector connection with a rectangular Cartesian coordinate system in space

Collinear condition of vectors in coordinates

Vector length and cosine guides

Solve the task on the vectors yourself, and then see the decision

Operations on vectors specified in coordinate form

Concept of vector in classical geometry

Addition of vectors

Vector difference

Location vectors

Vectors in physics

Vector in linear algebra and mathematical analysis

Projecting vectors

The simplest tasks of analytical geometry.
Actions with vectors in coordinates