Before giving the concept of a vector product, let us turn to the question of the orientation of the ordered triple of vectors a → , b → , c → in three-dimensional space.

To begin with, let's set aside the vectors a → , b → , c → from one point. The orientation of the triple a → , b → , c → is right or left, depending on the direction of the vector c → . From the direction in which the shortest turn is made from the vector a → to b → from the end of the vector c → , the form of the triple a → , b → , c → will be determined.

If the shortest rotation is counterclockwise, then the triple of vectors a → , b → , c → is called right if clockwise - left.

Next, take two non-collinear vectors a → and b → . Let us then postpone the vectors A B → = a → and A C → = b → from the point A. Let us construct a vector A D → = c → , which is simultaneously perpendicular to both A B → and A C → . Thus, when constructing the vector A D → = c →, we can do two things, giving it either one direction or the opposite (see illustration).

The ordered trio of vectors a → , b → , c → can be, as we found out, right or left depending on the direction of the vector.

From the above, we can introduce the definition of a vector product. This definition is given for two vectors defined in a rectangular coordinate system of three-dimensional space.

Definition 1

The vector product of two vectors a → and b → we will call such a vector given in a rectangular coordinate system of three-dimensional space such that:

• if the vectors a → and b → are collinear, it will be zero;
• it will be perpendicular to both vector a →​​ and vector b → i.e. ∠ a → c → = ∠ b → c → = π 2 ;
• its length is determined by the formula: c → = a → b → sin ∠ a → , b → ;
• the triplet of vectors a → , b → , c → has the same orientation as the given coordinate system.

The cross product of vectors a → and b → has the following notation: a → × b → .

Cross product coordinates

Since any vector has certain coordinates in the coordinate system, it is possible to introduce a second definition of the vector product, which will allow you to find its coordinates from the given coordinates of the vectors.

Definition 2

In a rectangular coordinate system of three-dimensional space vector product of two vectors a → = (a x ; a y ; a z) and b → = (b x ; b y ; b z) call the vector c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , where i → , j → , k → are coordinate vectors.

The vector product can be represented as a determinant of a square matrix of the third order, where the first row is the orta vectors i → , j → , k → , the second row contains the coordinates of the vector a → , and the third is the coordinates of the vector b → in a given rectangular coordinate system, this matrix determinant looks like this: c → = a → × b → = i → j → k → a x a y a z b x b y b z

Expanding this determinant over the elements of the first row, we obtain the equality: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z i → - a x a z b x b z j → + a x a y b x b y k → = = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →

Cross product properties

It is known that the vector product in coordinates is represented as the determinant of the matrix c → = a → × b → = i → j → k → a x a y a z b x b y b z , then on the base matrix determinant properties the following vector product properties:

1. anticommutativity a → × b → = - b → × a → ;
2. distributivity a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → or a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
3. associativity λ a → × b → = λ a → × b → or a → × (λ b →) = λ a → × b → , where λ is an arbitrary real number.

These properties have not complicated proofs.

For example, we can prove the anticommutativity property of a vector product.

Proof of anticommutativity

By definition, a → × b → = i → j → k → a x a y a z b x b y b z and b → × a → = i → j → k → b x b y b z a x a y a z . And if two rows of the matrix are interchanged, then the value of the determinant of the matrix should change to the opposite, therefore, a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y a z = - b → × a → , which and proves the anticommutativity of the vector product.

Vector Product - Examples and Solutions

In most cases, there are three types of tasks.

In problems of the first type, the lengths of two vectors and the angle between them are usually given, but you need to find the length of the cross product. In this case, use the following formula c → = a → b → sin ∠ a → , b → .

Example 1

Find the length of the cross product of vectors a → and b → if a → = 3 , b → = 5 , ∠ a → , b → = π 4 is known.

Solution

Using the definition of the length of the vector product of vectors a → and b →, we solve this problem: a → × b → = a → b → sin ∠ a → , b → = 3 5 sin π 4 = 15 2 2 .

Answer: 15 2 2 .

Tasks of the second type have a connection with the coordinates of vectors, they contain a vector product, its length, etc. are searched through the known coordinates of the given vectors a → = (a x ; a y ; a z) And b → = (b x ; b y ; b z) .

For this type of task, you can solve a lot of options for tasks. For example, not the coordinates of the vectors a → and b → , but their expansions in coordinate vectors of the form b → = b x i → + b y j → + b z k → and c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , or the vectors a → and b → can be given by the coordinates of their start and end points.

Consider the following examples.

Example 2

Two vectors are set in a rectangular coordinate system a → = (2 ; 1 ; - 3) , b → = (0 ; - 1 ; 1) . Find their vector product.

Solution

According to the second definition, we find the vector product of two vectors in given coordinates: a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → = = (1 1 - (- 3) (- 1)) i → + ((- 3) 0 - 2 1) j → + (2 (- 1) - 1 0) k → = = - 2 i → - 2 j → - 2 k → .

If we write the vector product through the matrix determinant, then the solution of this example is as follows: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k → .

Answer: a → × b → = - 2 i → - 2 j → - 2 k → .

Example 3

Find the length of the cross product of vectors i → - j → and i → + j → + k → , where i → , j → , k → - orts of a rectangular Cartesian coordinate system.

Solution

First, let's find the coordinates of the given vector product i → - j → × i → + j → + k → in the given rectangular coordinate system.

It is known that the vectors i → - j → and i → + j → + k → have coordinates (1 ; - 1 ; 0) and (1 ; 1 ; 1) respectively. Find the length of the vector product using the matrix determinant, then we have i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → .

Therefore, the vector product i → - j → × i → + j → + k → has coordinates (- 1 ; - 1 ; 2) in the given coordinate system.

We find the length of the vector product by the formula (see the section on finding the length of the vector): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6 .

Answer: i → - j → × i → + j → + k → = 6 . .

Example 4

The coordinates of three points A (1 , 0 , 1) , B (0 , 2 , 3) ​​, C (1 , 4 , 2) are given in a rectangular Cartesian coordinate system. Find some vector perpendicular to A B → and A C → at the same time.

Solution

Vectors A B → and A C → have the following coordinates (- 1 ; 2 ; 2) and (0 ; 4 ; 1) respectively. Having found the vector product of the vectors A B → and A C → , it is obvious that it is a perpendicular vector by definition to both A B → and A C → , that is, it is the solution to our problem. Find it A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → .

Answer: - 6 i → + j → - 4 k → . is one of the perpendicular vectors.

Problems of the third type are focused on using the properties of the vector product of vectors. After applying which, we will obtain a solution to the given problem.

Example 5

The vectors a → and b → are perpendicular and their lengths are 3 and 4 respectively. Find the length of the cross product 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b → .

Solution

By the distributivity property of the vector product, we can write 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →

By the property of associativity, we take out the numerical coefficients beyond the sign of vector products in the last expression: 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b → = = 3 a → × a → + 3 (- 2) a → × b → + (- 1) b → × a → + (- 1) (- 2) b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →

The vector products a → × a → and b → × b → are equal to 0, since a → × a → = a → a → sin 0 = 0 and b → × b → = b → b → sin 0 = 0 , then 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b → = - 6 a → × b → - b → × a → . .

From the anticommutativity of the vector product it follows - 6 a → × b → - b → × a → = - 6 a → × b → - (- 1) a → × b → = - 5 a → × b → . .

Using the properties of the vector product, we obtain the equality 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → .

By condition, the vectors a → and b → are perpendicular, that is, the angle between them is equal to π 2 . Now it remains only to substitute the found values ​​into the corresponding formulas: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → sin (a →, b →) = 5 3 4 sin π 2 = 60.

Answer: 3 a → - b → × a → - 2 b → = 60 .

The length of the cross product of vectors by definition is a → × b → = a → · b → · sin ∠ a → , b → . Since it is already known (from the school course) that the area of ​​a triangle is equal to half the product of the lengths of its two sides multiplied by the sine of the angle between these sides. Therefore, the length of the vector product is equal to the area of ​​a parallelogram - a doubled triangle, namely, the product of the sides in the form of vectors a → and b → , laid off from one point, by the sine of the angle between them sin ∠ a → , b → .

This is the geometric meaning of the vector product.

The physical meaning of the vector product

In mechanics, one of the branches of physics, thanks to the vector product, you can determine the moment of force relative to a point in space.

Definition 3

Under the moment of force F → , applied to point B , relative to point A we will understand the following vector product A B → × F → .

If you notice a mistake in the text, please highlight it and press Ctrl+Enter

Obviously, in the case of a cross product, the order in which the vectors are taken matters, moreover,

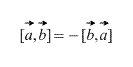
Also, directly from the definition it follows that for any scalar factor k (number) the following is true:

The cross product of collinear vectors is equal to the zero vector. Moreover, the cross product of two vectors is zero if and only if they are collinear. (In case one of them is a zero vector it is necessary to remember that the zero vector is collinear to any vector by definition).

Vector product has distributive property, that is

The expression of the cross product in terms of the coordinates of the vectors.

Let two vectors be given

(how to find the coordinates of a vector by the coordinates of its beginning and end - see the article Dot product of vectors, paragraph Alternative definition of the dot product, or calculating the dot product of two vectors given by their coordinates.)

Why do you need a vector product?

There are many ways to use the cross product, for example, as already written above, by calculating the cross product of two vectors, you can find out if they are collinear.

Or it can be used as a way to calculate the area of ​​a parallelogram built from these vectors. Based on the definition, the length of the resulting vector is the area of ​​this parallelogram.

Also, a huge number of applications exist in electricity and magnetism.

Online calculator of vector product.

To find the scalar product of two vectors using this calculator, you need to enter the coordinates of the first vector in the first line in order, and the second vector in the second. The coordinates of vectors can be calculated from their start and end coordinates (see article Dot product of vectors , item An alternative definition of the dot product, or calculating the dot product of two vectors given their coordinates.)

Angle between vectors

In order for us to introduce the concept of a cross product of two vectors, we must first deal with such a concept as the angle between these vectors.

Let us be given two vectors $\overline(α)$ and $\overline(β)$. Let us take some point $O$ in space and set aside the vectors $\overline(α)=\overline(OA)$ and $\overline(β)=\overline(OB)$ from it, then the angle $AOB$ will be called angle between these vectors (Fig. 1).

Notation: $∠(\overline(α),\overline(β))$

The concept of the cross product of vectors and the formula for finding

Definition 1

The vector product of two vectors is a vector perpendicular to both given vectors, and its length will be equal to the product of the lengths of these vectors with the sine of the angle between these vectors, and this vector with two initial ones has the same orientation as the Cartesian coordinate system.

Notation: $\overline(α)х\overline(β)$.

Mathematically it looks like this:

1. $|\overline(α)x\overline(β)|=|\overline(α)||\overline(β)|sin⁡∠(\overline(α),\overline(β))$
2. $\overline(α)x\overline(β)⊥\overline(α)$, $\overline(α)x\overline(β)⊥\overline(β)$
3. $(\overline(α)x\overline(β),\overline(α),\overline(β))$ and $(\overline(i),\overline(j),\overline(k))$ are the same oriented (Fig. 2)

Obviously, the outer product of vectors will equal the zero vector in two cases:

1. If the length of one or both vectors is zero.
2. If the angle between these vectors is equal to $180^\circ$ or $0^\circ$ (because in this case the sine is equal to zero).

To clearly see how the cross product of vectors is found, consider the following solution examples.

Example 1

Find the length of the vector $\overline(δ)$, which will be the result of the cross product of vectors, with coordinates $\overline(α)=(0,4,0)$ and $\overline(β)=(3,0,0 )$.

Solution.

Let's depict these vectors in the Cartesian coordinate space (Fig. 3):

Figure 3. Vectors in Cartesian coordinate space. Author24 - online exchange of student papers

We see that these vectors lie on the $Ox$ and $Oy$ axes, respectively. Therefore, the angle between them will be equal to $90^\circ$. Let's find the lengths of these vectors:

$|\overline(α)|=\sqrt(0+16+0)=4$

$|\overline(β)|=\sqrt(9+0+0)=3$

Then, by Definition 1, we obtain the module $|\overline(δ)|$

$|\overline(δ)|=|\overline(α)||\overline(β)|sin90^\circ=4\cdot 3\cdot 1=12$

Answer: $12$.

Calculation of the cross product by the coordinates of the vectors

Definition 1 immediately implies a way to find the cross product for two vectors. Since a vector, in addition to a value, also has a direction, it is impossible to find it only using a scalar value. But besides it, there is another way to find the vectors given to us using the coordinates.

Let us be given vectors $\overline(α)$ and $\overline(β)$, which will have coordinates $(α_1,α_2,α_3)$ and $(β_1,β_2,β_3)$, respectively. Then the vector of the cross product (namely, its coordinates) can be found by the following formula:

$\overline(α)x\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\α_1&α_2&α_3\\β_1&β_2&β_3\end(vmatrix)$

Otherwise, expanding the determinant, we obtain the following coordinates

$\overline(α)х\overline(β)=(α_2 β_3-α_3 β_2,α_3 β_1-α_1 β_3,α_1 β_2-α_2 β_1)$

Example 2

Find the vector of the cross product of collinear vectors $\overline(α)$ and $\overline(β)$ with coordinates $(0,3,3)$ and $(-1,2,6)$.

Solution.

Let's use the formula above. Get

$\overline(α)x\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\0&3&3\\-1&2&6\end(vmatrix)=(18 -6)\overline(i)-(0+3)\overline(j)+(0+3)\overline(k)=12\overline(i)-3\overline(j)+3\overline(k )=(12,-3,3)$

Answer: $(12,-3,3)$.

Properties of the cross product of vectors

For arbitrary mixed three vectors $\overline(α)$, $\overline(β)$ and $\overline(γ)$, as well as $r∈R$, the following properties hold:

Example 3

Find the area of ​​a parallelogram whose vertices have coordinates $(3,0,0)$, $(0,0,0)$, $(0,8,0)$ and $(3,8,0)$.

Solution.

First, draw this parallelogram in coordinate space (Fig. 5):

Figure 5. Parallelogram in coordinate space. Author24 - online exchange of student papers

We see that the two sides of this parallelogram are constructed using collinear vectors with coordinates $\overline(α)=(3,0,0)$ and $\overline(β)=(0,8,0)$. Using the fourth property, we get:

$S=|\overline(α)x\overline(β)|$

Find the vector $\overline(α)х\overline(β)$:

$\overline(α)x\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\3&0&0\\0&8&0\end(vmatrix)=0\overline (i)-0\overline(j)+24\overline(k)=(0,0,24)$

Hence

$S=|\overline(α)x\overline(β)|=\sqrt(0+0+24^2)=24$

7.1. Definition of cross product

Three non-coplanar vectors a , b and c , taken in the indicated order, form a right triple if from the end of the third vector c the shortest turn from the first vector a to the second vector b is seen to be counterclockwise, and a left one if clockwise (see Fig. . 16).

The vector product of a vector a and vector b is called vector c, which:

1. Perpendicular to vectors a and b, i.e. c ^ a and c ^ b;

2. It has a length numerically equal to the area of ​​the parallelogram built on the vectors a andb as on the sides (see fig. 17), i.e.

3. The vectors a , b and c form a right triple.

The vector product is denoted a x b or [a,b]. From the definition of a vector product, the following relations between the orts i follow directly, j And k(see fig. 18):

i x j \u003d k, j x k \u003d i, k x i \u003d j.
Let us prove, for example, that i xj \u003d k.

1) k ^ i , k ^ j;

2) |k |=1, but | i x j| = |i | |J| sin(90°)=1;

3) vectors i , j and k form a right triple (see Fig. 16).

7.2. Cross product properties

1. When the factors are rearranged, the vector product changes sign, i.e. and xb \u003d (b xa) (see Fig. 19).

Vectors a xb and b xa are collinear, have the same modules (the area of ​​the parallelogram remains unchanged), but are oppositely directed (triples a, b, a xb and a, b, b x a of opposite orientation). That is axb = -(bxa).

2. The vector product has a combination property with respect to a scalar factor, i.e. l ​​(a xb) \u003d (l a) x b \u003d a x (l b).

Let l >0. The vector l (a xb) is perpendicular to the vectors a and b. Vector ( l a)x b is also perpendicular to the vectors a and b(vectors a, l but lie in the same plane). So the vectors l(a xb) and ( l a)x b collinear. It is obvious that their directions coincide. They have the same length:

That's why l(a xb)= l a xb. It is proved similarly for l<0.

3. Two non-zero vectors a and b are collinear if and only if their vector product is equal to the zero vector, i.e., and ||b<=>and xb \u003d 0.

In particular, i *i =j *j =k *k =0 .

4. The vector product has a distribution property:

(a+b) xs = a xs + b xs .

Accept without proof.

7.3. Cross product expression in terms of coordinates

We will use the vector cross product table i , j and k :

if the direction of the shortest path from the first vector to the second coincides with the direction of the arrow, then the product is equal to the third vector, if it does not match, the third vector is taken with a minus sign.

Let two vectors a =a x i +a y j+az k and b=bx i+by j+bz k. Let's find the vector product of these vectors by multiplying them as polynomials (according to the properties of the vector product):

The resulting formula can be written even shorter:

since the right side of equality (7.1) corresponds to the expansion of the third-order determinant in terms of the elements of the first row. Equality (7.2) is easy to remember.

7.4. Some applications of the cross product

Establishing collinearity of vectors

Finding the area of ​​a parallelogram and a triangle

According to the definition of the cross product of vectors A and b |a xb | =| a | * |b |sin g , i.e. S par = |a x b |. And, therefore, D S \u003d 1/2 | a x b |.

Determining the moment of force about a point

Let a force be applied at point A F =AB let it go ABOUT- some point in space (see Fig. 20).

It is known from physics that torque F relative to the point ABOUT called vector M , which passes through the point ABOUT And:

1) perpendicular to the plane passing through the points O, A, B;

2) numerically equal to the product of the force and the arm

3) forms a right triple with vectors OA and A B .

Therefore, M \u003d OA x F.

Finding the linear speed of rotation

Speed v point M of a rigid body rotating at an angular velocity w around a fixed axis, is determined by the Euler formula v \u003d w x r, where r \u003d OM, where O is some fixed point of the axis (see Fig. 21).

Using the Cross Product of VECTORS

to calculate the area

some geometric shapes

Research work in mathematics

Pupil 10 B class

MOU secondary school №73

Perevoznikov Mikhail

Leaders:

Mathematics teacher MOU secondary school №73 Dragunova Svetlana Nikolaevna

Department assistant. Mathematical Analysis of the Faculty of Mechanics and Mathematics, SSU N.G. Chernyshevsky Berdnikov Gleb Sergeevich

Saratov, 2015

Introduction.

1. Theoretical review.

1.1. Vectors and calculations with vectors.

1.2. Using the scalar product of vectors in solving problems

1.3 Dot product of vectors in coordinates

1.4. Vector product of vectors in three-dimensional Euclidean space: definition of the concept.

1.5. Vector coordinates products of vectors.

2. Practical part.

2.1. Relationship between the cross product and the area of ​​a triangle and a parallelogram. Derivation of the formula and the geometric meaning of the vector product of vectors.

2.2. Knowing only the coordinates of the points, find the area of ​​the triangle. Proof of the theorem

2.3. Checking on examples the correctness of the formula.

2.4. Practical use of vector algebra and product of vectors.

Conclusion

Introduction

As you know, many geometric problems have two key solutions - graphical and analytical. The graphic method is associated with the construction of graphs and drawings, and the analytical method involves solving problems mainly with the help of algebraic operations. In the latter case, the algorithm for solving problems is related to analytical geometry. Analytic geometry is a branch of mathematics, or rather linear algebra, which considers the solution of geometric problems by means of algebra based on the method of coordinates on the plane and in space. Analytical geometry allows you to analyze geometric images, explore lines and surfaces that are important for practical applications. Moreover, in this science, in order to expand the spatial understanding of figures, in addition, the vector product of vectors is sometimes used.

Due to the widespread use of three-dimensional spatial technologies, the study of the properties of some geometric shapes using a vector product seems relevant.

In this regard, the purpose of this project was identified - the use of the cross product of vectors to calculate the area of ​​some geometric shapes.

In connection with this goal, the following tasks were solved:

1. Theoretically study the necessary foundations of vector algebra and define the vector product of vectors in a coordinate system;

2. Analyze the presence of a connection between a vector product and the area of ​​a triangle and a parallelogram;

3. Derive the formula for the area of ​​a triangle and a parallelogram in coordinates;

4. Check on specific examples the correctness of the derived formula.

1. Theoretical review.

1. Vectors and calculations with vectors

A vector is a directed segment, for which its beginning and end are indicated:

In this case, the beginning of the segment is the point A, the end of the segment is a point IN. The vector itself is denoted by
or . To find the coordinates of a vector
, knowing the coordinates of its start points A and end point B, it is necessary to subtract the corresponding coordinates of the start point from the coordinates of the end point:

= { B x -A x ; B y -A y }

Vectors that lie on parallel lines or on the same line are called collinear. In this case, the vector is a segment characterized by length and direction.

The length of the directed segment determines the numerical value of the vector and is called the length of the vector or the modulus of the vector.

Vector length || in rectangular Cartesian coordinates is equal to the square root of the sum of the squares of its coordinates.

Vectors can be manipulated in many ways.

For example, addition. To add them, you first need to draw the second vector from the end of the first, and then connect the beginning of the first to the end of the second (Fig. 1). The sum of the vectors is another vector with new coordinates.

The sum of vectors = {a x ; a y) And = {b x ; b y) can be found using the following formula:

+ = (a x +b x ; a y +b y }

Rice. 1. Actions with vectors

When subtracting vectors, you must first draw them from one point, and then connect the end of the second to the end of the first.

Vector difference = {a x ; a y) And = {b x ; b y } can be found using the formula:

- = { a x -b x ; a y -b y }

Also, vectors can be multiplied by a number. The result will also be a vector that is k times larger (or smaller) than the given one. Its direction will depend on the sign of k: if k is positive, the vectors are in the same direction, and if k is negative, they are oppositely directed.

Vector product = {a x ; a y } and the number k can be found using the following formula:

k = (k a x ; k a y }

Is it possible to multiply a vector by a vector? Of course, and even two options!

The first option is the scalar product.

Rice. 2. Dot product in coordinates

To find the product of vectors, you can use the angle  between these vectors, shown in Figure 3.

It follows from the formula that the scalar product is equal to the product of the lengths of these vectors and the cosine of the angle between them, its result is a number. It is important that if the vectors are perpendicular, then their scalar product is equal to zero, because the cosine of the right angle between them is zero.

In the coordinate plane, the vector also has coordinates. IN vectors, their coordinates, and the dot product are some of the most convenient methods for calculating the angle between lines (or their segments) if a coordinate system is entered.And if the coordinates
, then their scalar product is:

In three-dimensional space, there are 3 axes and, accordingly, points and vectors in such a system will have 3 coordinates each, and the scalar product of vectors is calculated by the formula:

1.2. Vector product of vectors in three-dimensional space.

The second option for calculating the product of vectors is the vector product. But in order to determine it, it is no longer a plane that is required, but a three-dimensional space in which the beginning and end of the vector have 3 coordinates each.

In contrast to the scalar product of vectors in three-dimensional space, the “vector multiplication” operation on vectors leads to a different result. If in the previous case of scalar multiplication of two vectors the result was a number, then in the case of vector multiplication of vectors the result will be another vector perpendicular to both vectors that entered into the product. Therefore, this product of vectors is called a vector product.

Obviously, when constructing the resulting vector , perpendicular to the two that entered the product - and , two opposite directions can be chosen. In this case, the direction of the resulting vector is determined by the rule of the right hand, or the gimlet rule. If you draw the vectors so that their beginnings coincide and rotate the first multiplier vector in the shortest way to the second multiplier vector, and four fingers of the right hand show the direction of rotation (as if covering a rotating cylinder), then a protruding thumb will show the direction of the product vector (Fig. 7).

Rice. 7. Right hand rule

1.3. Properties of the cross product of vectors.

The length of the resulting vector is determined by the formula

.

Wherein
vector product. As mentioned above, the resulting vector will be perpendicular
, and its direction is determined by the right hand rule.

The vector product depends on the order of the factors, namely:

The cross product of non-zero vectors is 0 if they are collinear, then the sine of the angle between them will be 0.

The coordinates of vectors in three-dimensional space are expressed as follows: . Then the coordinates of the resulting vector are found by the formula

The length of the resulting vector is found by the formula:

.

2. Practical part.

2.1. Connection of the vector product with the area of ​​a triangle and a parallelogram in a plane. The geometric meaning of the cross product of vectors.

Let us be given a triangle ABC (Fig. 8). It is known that .

If we represent the sides of the triangle AB and AC as two vectors, then in the triangle area formula we find the expression for the cross product of vectors:

From the above, we can determine the geometric meaning of the vector product (Fig. 9):

the length of the cross product of vectors is equal to twice the area of ​​a triangle with sides of the vectors and , if they are set aside from one point.

In other words, the length of the cross product of vectors and is equal to the area of ​​the parallelogram,built on vectors And , with sides and and an angle between them equal to .

Rice. 9. The geometric meaning of the vector product of vectors

In this regard, we can give another definition of the vector product of vectors :

Cross product of a vector on a vector is called a vector , whose length is numerically equal to the area of ​​the parallelogram built on the vectors and , perpendicular to the plane of these vectors and directed so that the least rotation from k around vector was carried out counterclockwise when viewed from the end of the vector (Fig. 10).

Rice. 10. Definition of the cross product of vectors

using a parallelogram

2.2. Derivation of a formula for finding the area of ​​a triangle in coordinates.

So, we are given a triangle ABC in the plane and the coordinates of its vertices. Let's find the area of ​​this triangle (Fig. 11).

Rice. 11. An example of solving the problem of finding the area of ​​a triangle by the coordinates of its vertices

Solution.

First, consider the coordinates of the vertices in space and calculate the coordinates of the vectors AB and AC.

According to the formula given above, we calculate the coordinates of their vector product. The length of this vector is equal to 2 areas of the triangle ABC. The area of ​​a triangle is 10.

Moreover, if we consider a triangle on a plane, then the first 2 coordinates of the vector product will always be zero, so we can formulate the following theorem.

Theorem: Let a triangle ABC be given and the coordinates of its vertices (Fig. 12).

Then .

Rice. 12. Proof of the theorem

Proof.

Consider points in space and calculate the coordinates of the vectors BC and BA. . Using the above formula, we calculate the coordinates of the cross product of these vectors. Note that all terms containingz 1 or z 2 are equal to 0, because z 1i z 2 = 0. REMOVE!!!

So, therefore,

2.3. Checking the correctness of the formula on examples

Find the area of ​​a triangle formed by vectors a = (-1; 2; -2) and b = (2; 1; -1).

Solution: Let's find the cross product of these vectors:

a ×b=

I(2 (-1) - (-2) 1) - j((-1) (-1) - (-2) 2) + k((-1) 1 - 2 2) =

I(-2 + 2) - j(1 + 4) + k(-1 - 4) = -5 j - 5 k = (0; -5; -5)

From the properties of the vector product:

SΔ =

| a×b| =

√ 02 + 52 + 52 =

√ 25 + 25 =

√ 50 =

5√ 2

Answer: SΔ = 2.5√2.

Conclusion

2.4. Applications of vector algebra

and the scalar and cross product of vectors.

Where are vectors needed? Vector space and vectors are not only theoretical, but also have a very real practical application in the modern world.

In mechanics and physics, many quantities have not only a numerical value, but also a direction. Such quantities are called vector quantities. Together with the use of elementary mechanical concepts, based on their physical meaning, many quantities are considered as sliding vectors, and their properties are described both by axioms, as is customary in theoretical mechanics, and with the help of the mathematical properties of vectors. The most striking examples of vector quantities are speed, momentum and force (Fig. 12). For example, the angular momentum and the Lorentz force are mathematically written using vectors.

In physics, not only the vectors themselves are important, but their products are also important to a large extent, which help to calculate some quantities. The cross product is useful for determining the collinearity of vectors. The modulus of the cross product of two vectors is equal to the product of their moduli if they are perpendicular, and decreases to zero if the vectors are co-directed or oppositely directed.

As another example, the dot product is used to calculate work using the formula below, where F is the force vector and s is the displacement vector.

One example of using the product of vectors is the moment of force, which is equal to the product of the radius vector drawn from the axis of rotation to the point of application of the force and the vector of this force.

Much of what is calculated in physics by the right hand rule is a cross product. Find evidence, give examples.

It is also worth noting that the possible variants of vector spaces are not limited to two-dimensional and three-dimensional space. Higher mathematics considers spaces of higher dimensions, in which analogues of formulas for the scalar and vector products are also defined. Despite the fact that spaces of greater dimensions than 3, the human mind is unable to visualize, they surprisingly find applications in many areas of science and industry.

At the same time, the result of the cross product of vectors in three-dimensional Euclidean space is not a number, but the resulting vector with its own coordinates, direction, and length.

The direction of the resulting vector is determined by the right hand rule, which is one of the most surprising provisions of analytic geometry.

The cross product of vectors can be used to find the area of ​​a triangle or parallelogram given the coordinates of the vertices, which was confirmed by deriving a formula, proving a theorem, and solving practical problems.

Vectors are widely used in physics, where such indicators as speed, momentum and force can be represented as vector quantities and calculated geometrically.

List of sources used

Atanasyan L. S., Butuzov V. F., Kadomtsev S. B. et al. Geometry. Grades 7-9: a textbook for educational institutions. M.: , 2013. 383 p.

Atanasyan L.S., Butuzov V.F., Kadomtsev S.B. et al. Geometry. Grades 10-11: a textbook for educational organizations: basic and profile levels. M.: , 2013. 255 p.

Bugrov Ya.S., Nikolsky S.M. Higher Mathematics. Volume One: Elements of Linear Algebra and Analytic Geometry.

Kletenik D.V. Collection of problems in analytical geometry. Moscow: Nauka, Fizmatlit, 1998.

Analytic geometry.

Mathematics. Clover.

Learning mathematics online.

http://ru.onlinemschool.com/math/library/vector/multiply1/

Website of V. Glaznev.

http://glaznev.sibcity.ru/1kurs/analit/common/html/anlek7.htm

Wikipedia.

https://ru.wikipedia.org/wiki/%C2%E5%EA%F2%EE%F0%ED%EE%E5_%EF%F0%EE%E8%E7%E2%E5%E4%E5%ED %E8%E5