Antes de dar el concepto de producto vectorial, pasemos a la cuestión de la orientación de un triplete ordenado de vectores a →, b →, c → en el espacio tridimensional.

Dejemos de lado para el principio los vectores a →, b →, c → de un punto. La orientación de la triple a →, b →, c → puede ser derecha o izquierda, dependiendo de la dirección del vector c → mismo. A partir de la dirección en la que se realiza la rotación más corta desde el vector a → ab → desde el final del vector c →, se determinará la forma del triple a →, b →, c →.

Si la rotación más corta es en sentido antihorario, entonces el triplete de vectores a →, b →, c → se llama Derecha si en el sentido de las agujas del reloj - izquierda.

A continuación, tome dos vectores no colineales a → y b →. Pospongamos entonces los vectores A B → = a → y A C → = b → desde el punto A. Construimos un vector A D → = c →, que es simultáneamente perpendicular tanto a A B → como a A C →. Por lo tanto, al construir el vector en sí A D → = c → podemos hacer dos cosas, dándole una dirección o la opuesta (ver ilustración).

La triple ordenada de los vectores a →, b →, c → puede ser, como descubrimos, derecha o izquierda, dependiendo de la dirección del vector.

De lo anterior, podemos introducir la definición de un producto cruzado. Esta definición se da para dos vectores definidos en un sistema de coordenadas rectangular de espacio tridimensional.

Definición 1

El producto vectorial de dos vectores a → y b → llamaremos a dicho vector dado en un sistema de coordenadas rectangular de espacio tridimensional tal que:

si los vectores a → y b → son colineales, será cero;
será perpendicular tanto al vector a → como al vector b → es decir ∠ a → c → = ∠ b → c → = π 2;
su longitud está determinada por la fórmula: c → = a → b → sin ∠ a →, b →;
el triplete de vectores a →, b →, c → tiene la misma orientación que el sistema de coordenadas dado.

El producto vectorial de los vectores a → y b → tiene la siguiente notación: a → × b →.

Coordenadas de productos vectoriales

Dado que cualquier vector tiene ciertas coordenadas en el sistema de coordenadas, puede ingresar la segunda definición del producto cruzado, que le permitirá encontrar sus coordenadas por las coordenadas dadas de los vectores.

Definición 2

En un sistema de coordenadas rectangular de espacio tridimensional producto vectorial de dos vectores a → = (a x; a y; a z) y b → = (b x; b y; b z) llamado el vector c → = a → × b → = (ay bz - az by) i → + (az bx - ax bz) j → + (ax by - ay bx) k →, donde i →, j →, k → son vectores de coordenadas.

El producto vectorial se puede representar como el determinante de una matriz cuadrada de tercer orden, donde la primera fila son los vectores de los vectores unitarios i →, j →, k →, la segunda fila contiene las coordenadas del vector a →, y el tercero contiene las coordenadas del vector b → en un sistema de coordenadas rectangular dado, este determinante de la matriz se ve así: c → = a → × b → = i → j → k → axayazbxbybz

Expandiendo este determinante sobre los elementos de la primera fila, obtenemos la igualdad: c → = a → × b → = i → j → k → axayazbxbybz = ayazbybz i → - axazbxbz j → + axaybxby k → = = a → × b → = (ay bz - az by) i → + (az bx - ax bz) j → + (ax by - ay bx) k →

Propiedades del producto vectorial

Se sabe que el producto vectorial en coordenadas se representa como el determinante de la matriz c → = a → × b → = i → j → k → a x a y a z b x b y b z, luego sobre la base propiedades del determinante de la matriz muestra lo siguiente propiedades del producto vectorial:

anticomutatividad a → × b → = - b → × a →;
distributividad a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → o a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) →;
asociatividad λ a → × b → = λ a → × b → o a → × (λ b →) = λ a → × b →, donde λ es un número real arbitrario.

Estas propiedades no son difíciles de probar.

Como ejemplo, podemos probar la propiedad anti-conmutatividad de un producto vectorial.

Prueba de anticomutatividad

Por definición, a → × b → = i → j → k → a x a y a z b x b y b z y b → × a → = i → j → k → b x b y b z a x a y a z. Y si se reorganizan dos filas de la matriz, entonces el valor del determinante de la matriz debe cambiar al opuesto, por lo tanto, a → × b → = i → j → k → axayazbxbybz = - i → j → k → bxbybzaxayaz = - b → × a →, que y prueba la anti-conmutatividad del producto vectorial.

Producto vectorial - ejemplos y soluciones

En la mayoría de los casos, hay tres tipos de tareas.

En los problemas del primer tipo, normalmente se dan las longitudes de dos vectores y el ángulo entre ellos, pero es necesario encontrar la longitud del producto cruzado. En este caso, use la siguiente fórmula c → = a → b → sin ∠ a →, b →.

Ejemplo 1

Encuentre la longitud del producto vectorial de los vectores a → y b → si conoce a → = 3, b → = 5, ∠ a →, b → = π 4.

Solución

Al determinar la longitud del producto vectorial de los vectores a → y b → resolveremos este problema: a → × b → = a → b → sin ∠ a →, b → = 3 5 sin π 4 = 15 2 2.

Respuesta: 15 2 2 .

Los problemas del segundo tipo tienen relación con las coordenadas de los vectores, en ellos el producto cruzado, su longitud, etc. se buscan a través de las coordenadas conocidas de los vectores dados a → = (a x; a y; a z) y segundo → = (segundo x; segundo y; segundo z) .

Para este tipo de tarea, puede resolver muchas opciones para tareas. Por ejemplo, no se pueden dar las coordenadas de los vectores a → y b →, sino sus expansiones en vectores coordinados de la forma b → = segundo x yo → + segundo y j → + segundo z k → y c → = a → × b → = (ay bz - az by) i → + (az bx - ax bz) j → + (ax by - ay bx) k →, o los vectores a → y b → se pueden especificar por las coordenadas de sus puntos inicial y final.

Considere los siguientes ejemplos.

Ejemplo 2

En un sistema de coordenadas rectangular, se dan dos vectores a → = (2; 1; - 3), b → = (0; - 1; 1). Encuentra su producto cruzado.

Solución

Por la segunda definición, encontramos el producto vectorial de dos vectores en las coordenadas dadas: a → × b → = (ay bz - az by) i → + (az bx - ax bz) j → + (ax by - ay Bx ) k → = = (1 1 - (- 3) (- 1)) i → + ((- 3) 0 - 2 1) j → + (2 (- 1) - 1 0) k → = = - 2 i → - 2 j → - 2 k →.

Si escribimos el producto vectorial a través del determinante de la matriz, entonces la solución de este ejemplo se ve así: a → × b → = i → j → k → axayazbxbybz = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k →.

Respuesta: a → × b → = - 2 i → - 2 j → - 2 k →.

Ejemplo 3

Encuentre la longitud del producto vectorial de los vectores i → - j → e i → + j → + k →, donde i →, j →, k → son los vectores unitarios de un sistema de coordenadas cartesiano rectangular.

Solución

Primero, encontramos las coordenadas del producto vectorial dado i → - j → × i → + j → + k → en el sistema de coordenadas rectangular dado.

Se sabe que los vectores i → - j → e i → + j → + k → tienen coordenadas (1; - 1; 0) y (1; 1; 1), respectivamente. Encontremos la longitud del producto vectorial usando el determinante de la matriz, entonces tenemos i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → ...

Por lo tanto, el producto vectorial i → - j → × i → + j → + k → tiene coordenadas (- 1; - 1; 2) en el sistema de coordenadas dado.

Encontramos la longitud del producto vectorial mediante la fórmula (consulte la sección sobre cómo encontrar la longitud de un vector): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6.

Respuesta: i → - j → × i → + j → + k → = 6. ...

Ejemplo 4

En un sistema de coordenadas cartesiano rectangular, se dan las coordenadas de tres puntos A (1, 0, 1), B (0, 2, 3), C (1, 4, 2). Encuentra algún vector perpendicular a A B → y A C → al mismo tiempo.

Solución

Los vectores A B → y A C → tienen las siguientes coordenadas (- 1; 2; 2) y (0; 4; 1), respectivamente. Habiendo encontrado el producto vectorial de los vectores A B → y A C →, es obvio que es un vector perpendicular por definición tanto a A B → como a A C →, es decir, es una solución a nuestro problema. Encontrámoslo A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k →.

Respuesta: - 6 i → + j → - 4 k →. - uno de los vectores perpendiculares.

Los problemas del tercer tipo se centran en el uso de las propiedades del vector producto de vectores. Tras aplicar la cual, obtendremos una solución al problema planteado.

Ejemplo 5

Los vectores a → y b → son perpendiculares y sus longitudes son 3 y 4, respectivamente. Encuentre la longitud del producto vectorial 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →.

Solución

Por la propiedad de distributividad de un producto vectorial, podemos escribir 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →

Por la propiedad de asociatividad, movemos los coeficientes numéricos fuera del signo de los productos vectoriales en la última expresión: 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 segundo → = = 3 a → × a → + 3 (- 2) a → × b → + (- 1) b → × a → + (- 1) (- 2) b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →

Los productos vectoriales a → × a → y b → × b → son 0 porque a → × a → = a → a → sin 0 = 0 y b → × b → = b → b → sin 0 = 0, luego 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b → = - 6 a → × b → - b → × a →. ...

La anticomutatividad del producto vectorial implica - 6 a → × b → - b → × a → = - 6 a → × b → - (- 1) a → × b → = - 5 a → × b →. ...

Usando las propiedades del producto vectorial, obtenemos la igualdad 3 a → - b → × a → - 2 b → = = - 5 a → × b →.

Por hipótesis, los vectores a → y b → son perpendiculares, es decir, el ángulo entre ellos es π 2. Ahora solo queda sustituir los valores encontrados en las fórmulas correspondientes: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → · sin (a →, b →) = 5 · 3 · 4 · sin π 2 = 60.

Respuesta: 3 a → - b → × a → - 2 b → = 60.

La longitud del producto vectorial de vectores por orden es igual a a → × b → = a → b → sin ∠ a →, b →. Dado que ya se sabe (del curso escolar) que el área de un triángulo es igual a la mitad del producto de las longitudes de sus dos lados multiplicado por el seno del ángulo entre estos lados. Por lo tanto, la longitud del producto vectorial es igual al área del paralelogramo: el triángulo duplicado, es decir, el producto de los lados en la forma de los vectores a → y b →, trazados desde un punto, por el seno del ángulo entre ellos sin ∠ a →, b →.

Este es el significado geométrico del producto vectorial.

El significado físico de un producto vectorial.

En mecánica, una de las ramas de la física, gracias al producto vectorial, se puede determinar el momento de fuerza relativo a un punto en el espacio.

Definición 3

Por el momento de la fuerza F → aplicada al punto B, en relación con el punto A, nos referimos al siguiente producto vectorial A B → × F →.

Si nota un error en el texto, selecciónelo y presione Ctrl + Enter

Obviamente, en el caso de un producto cruzado, el orden en el que se toman los vectores importa; además,

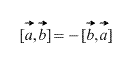
Además, directamente de la definición se deduce que para cualquier factor escalar k (número) se cumple lo siguiente:

El producto cruzado de los vectores colineales es igual al vector cero. Además, el producto cruzado de dos vectores es cero si y solo si son colineales. (En caso de que uno de ellos sea un vector cero, recuerde que el vector cero es colineal con cualquier vector por definición).

El producto vectorial tiene propiedad de distribución, es decir

Expresión del producto cruzado en términos de las coordenadas de los vectores.

Que se den dos vectores

(cómo encontrar las coordenadas de un vector por las coordenadas de su principio y final; consulte el artículo Producto escalar de vectores, párrafo Definición alternativa del producto escalar o cálculo del producto escalar de dos vectores dados por sus coordenadas).

¿Por qué producto cruzado?

Hay muchas formas de usar el producto cruzado, por ejemplo, como ya se escribió anteriormente, calculando el producto cruzado de dos vectores, puede averiguar si son colineales.

O puede usarse como una forma de calcular el área de un paralelogramo construido sobre estos vectores. Según la definición, la longitud del vector resultante es el área de este paralelogramo.

También hay una gran cantidad de aplicaciones en electricidad y magnetismo.

Calculadora de productos vectoriales en línea.

Para encontrar el producto escalar de dos vectores con esta calculadora, debe ingresar en la primera línea en orden las coordenadas del primer vector, en el segundo, el segundo. Las coordenadas de los vectores se pueden calcular mediante las coordenadas de su inicio y final (ver artículo Producto escalar de vectores, elemento Definición alternativa de producto escalar o cálculo del producto escalar de dos vectores dados por sus coordenadas.)

Ángulo entre vectores

Para que podamos introducir el concepto del producto cruzado de dos vectores, primero debemos entender un concepto como el ángulo entre estos vectores.

Vamos a tener dos vectores $ \ overline (α) $ y $ \ overline (β) $. Toma algún punto $ O $ en el espacio y aparta los vectores $ \ overline (α) = \ overline (OA) $ y $ \ overline (β) = \ overline (OB) $, entonces el ángulo $ AOB $ será llamado ángulo entre estos vectores (Fig. 1).

Notación: $ ∠ (\ overline (α), \ overline (β)) $

El concepto de un producto vectorial de vectores y la fórmula para encontrar

Definición 1

El vector producto de dos vectores es un vector perpendicular a ambos vectores dados, y su longitud será igual al producto de las longitudes de estos vectores por el seno del ángulo entre estos vectores, y este vector con dos iniciales tiene la misma orientación como el sistema de coordenadas cartesianas.

Notación: $ \ overline (α) x \ overline (β) $.

Matemáticamente, se ve así:

$ | \ overline (α) x \ overline (β) | = | \ overline (α) || \ overline (β) | sin⁡∠ (\ overline (α), \ overline (β)) $
$ \ overline (α) x \ overline (β) ⊥ \ overline (α) $, $ \ overline (α) x \ overline (β) ⊥ \ overline (β) $
$ (\ overline (α) x \ overline (β), \ overline (α), \ overline (β)) $ y $ (\ overline (i), \ overline (j), \ overline (k)) $ son igual orientado (fig.2)

Obviamente, el producto externo de los vectores será igual al vector cero en dos casos:

Si la longitud de uno o ambos vectores es cero.
Si el ángulo entre estos vectores es $ 180 ^ \ circ $ o $ 0 ^ \ circ $ (ya que en este caso el seno es cero).

Para ver claramente cómo se calcula el producto vectorial de los vectores, considere los siguientes ejemplos de soluciones.

Ejemplo 1

Encuentra la longitud del vector $ \ overline (δ) $, que será el resultado del producto vectorial de vectores, con coordenadas $ \ overline (α) = (0,4,0) $ y $ \ overline (β) = (3,0,0) $.

Solución.

Representemos estos vectores en el espacio de coordenadas cartesianas (Fig.3):

Figura 3. Vectores en el espacio de coordenadas cartesianas. Author24 - intercambio en línea de trabajos de estudiantes

Vemos que estos vectores se encuentran en los ejes $ Ox $ y $ Oy $, respectivamente. Por lo tanto, el ángulo entre ellos será igual a $ 90 ^ \ circ $. Encontremos las longitudes de estos vectores:

$ | \ overline (α) | = \ sqrt (0 + 16 + 0) = 4 $

$ | \ overline (β) | = \ sqrt (9 + 0 + 0) = 3 $

Entonces, por la Definición 1, obtenemos el módulo $ | \ overline (δ) | $

$ | \ overline (δ) | = | \ overline (α) || \ overline (β) | sin90 ^ \ circ = 4 \ cdot 3 \ cdot 1 = 12 $

Respuesta: $ 12 $.

Cálculo del producto cruzado por las coordenadas de los vectores.

La definición 1 implica inmediatamente un método para encontrar un producto vectorial para dos vectores. Dado que un vector, además de su valor, también tiene una dirección, es imposible encontrarlo solo con la ayuda de una cantidad escalar. Pero además de eso, también hay una forma de encontrar vectores usando las coordenadas de los vectores.

Déjenos los vectores $ \ overline (α) $ y $ \ overline (β) $, que tendrán las coordenadas $ (α_1, α_2, α_3) $ y $ (β_1, β_2, β_3) $, respectivamente. Entonces, el vector del producto vectorial (es decir, sus coordenadas) se puede encontrar mediante la siguiente fórmula:

$ \ overline (α) x \ overline (β) = \ begin (vmatrix) \ overline (i) & \ overline (j) & \ overline (k) \\ α_1 & α_2 & α_3 \\ β_1 & β_2 & β_3 \ fin (vmatrix) $

De lo contrario, expandiendo el determinante, obtenemos las siguientes coordenadas

$ \ overline (α) х \ overline (β) = (α_2 β_3-α_3 β_2, α_3 β_1-α_1 β_3, α_1 β_2-α_2 β_1) $

Ejemplo 2

Encuentre el vector del producto vectorial de los vectores colineales $ \ overline (α) $ y $ \ overline (β) $ con coordenadas $ (0,3,3) $ y $ (- 1,2,6) $.

Solución.

Usemos la fórmula anterior. Obtenemos

$ \ overline (α) x \ overline (β) = \ begin (vmatrix) \ overline (i) & \ overline (j) & \ overline (k) \\ 0 & 3 & 3 \\ - 1 & 2 & 6 \ end (vmatrix) = (18-6) \ overline (i) - (0 + 3) \ overline (j) + (0 + 3) \ overline (k) = 12 \ overline (i) -3 \ overline ( j) +3 \ overline (k) = (12, -3.3) $

Respuesta: $ (12, -3.3) $.

Propiedades del producto vectorial

Para tres vectores mixtos arbitrarios $ \ overline (α) $, $ \ overline (β) $ y $ \ overline (γ) $, así como $ r∈R $, se cumplen las siguientes propiedades:

Ejemplo 3

Encuentre el área de un paralelogramo cuyos vértices están en las coordenadas $ (3,0,0) $, $ (0,0,0) $, $ (0,8,0) $ y $ (3,8, 0) $.

Solución.

Primero, representaremos este paralelogramo en el espacio de coordenadas (Fig.5):

Figura 5. Paralelogramo en el espacio de coordenadas. Author24 - intercambio en línea de trabajos de estudiantes

Vemos que los dos lados de este paralelogramo se construyen usando vectores colineales con coordenadas $ \ overline (α) = (3,0,0) $ y $ \ overline (β) = (0,8,0) $. Usando la cuarta propiedad, obtenemos:

$ S = | \ overline (α) x \ overline (β) | $

Encuentre el vector $ \ overline (α) x \ overline (β) $:

$ \ overline (α) x \ overline (β) = \ begin (vmatrix) \ overline (i) & \ overline (j) & \ overline (k) \\ 3 & 0 & 0 \\ 0 & 8 & 0 \ end (vmatrix) = 0 \ overline (i) -0 \ overline (j) +24 \ overline (k) = (0,0,24) $

Por eso

$ S = | \ overline (α) x \ overline (β) | = \ sqrt (0 + 0 + 24 ^ 2) = 24 $

7.1. Definición de un producto cruzado

Tres vectores no coplanares a, byc, tomados en el orden indicado, forman un triplete recto si, desde el final del tercer vector c, la rotación más corta desde el primer vector a hasta el segundo vector b se ve en sentido antihorario, y la izquierda, si es en el sentido de las agujas del reloj (ver Fig. 16).

El producto vectorial de un vector a por un vector b es un vector c, que:

1. Perpendicular a los vectores a y b, es decir, c ^ a y c ^ B;

2. Tiene una longitud numéricamente igual al área de un paralelogramo construido sobre los vectores ayB como en los lados (ver fig. 17), es decir.

3. Los vectores a, byc forman un triplete a la derecha.

El producto cruzado se denota a x bo [a, b]. La definición de un producto vectorial implica directamente las siguientes relaciones entre los vectores i, j y k(ver fig.18):

yo x j = k, j x k = yo, k x yo = j.
Demostremos, por ejemplo, que i хj = k.

1) k ^ yo, k ^ j;

2) | k | = 1, pero | yo x j| = | yo | | J | sen (90 °) = 1;

3) vectores i, j y k formar un triplete a la derecha (ver Fig. 16).

7.2. Propiedades del producto vectorial

1. Cuando se reordenan los factores, el producto vectorial cambia de signo; a xb = (b xa) (vea la figura 19).

Los vectores a xb y b son colineales, tienen los mismos módulos (el área del paralelogramo permanece sin cambios), pero direcciones opuestas (triplica a, b, a xb y a, b, b x a de orientación opuesta). Es decir una xb = -(b xa).

2. El producto vectorial posee la propiedad combinatoria con respecto al factor escalar, es decir, l (а хb) = (l а) х b = а х (l b).

Sea l> 0. El vector l (a xb) es perpendicular a los vectores ay b. Vector ( l a) x B también es perpendicular a los vectores ay B(vectores a, l y yacen en el mismo plano). De ahí los vectores l(a xb) y ( l a) x B colineal. Evidentemente, sus direcciones coinciden. Tienen la misma longitud:

Es por eso l(a хb) = l a xb. Se puede probar de manera similar para l<0.

3. Dos vectores distintos de cero ay B colineal si y solo si su producto cruzado es igual al vector cero, es decir, a || b<=>a xb = 0.

En particular, i * i = j * j = k * k = 0.

4. El producto vectorial tiene la propiedad de distribución:

(a + b) xc = a xc + B xc.

Lo aceptaremos sin prueba.

7.3. Expresión del producto cruzado en términos de coordenadas

Usaremos la tabla de productos cruzados de los vectores i, j y k:

si la dirección del camino más corto desde el primer vector al segundo coincide con la dirección de la flecha, entonces el producto es igual al tercer vector, si no, el tercer vector se toma con un signo menos.

Sean dos vectores a = a x i + a y j+ una z k y b = b x I+ por j+ b z k... Encontremos el producto cruzado de estos vectores, multiplicándolos como polinomios (según las propiedades del producto cruzado):

La fórmula resultante se puede escribir aún más corta:

dado que el lado derecho de la igualdad (7.1) corresponde a la expansión del determinante de tercer orden en términos de los elementos de la primera fila, la igualdad (7.2) es fácil de recordar.

7.4. Algunas aplicaciones del trabajo vectorial

Establecer vectores colineales

Hallar el área de un paralelogramo y un triángulo

Según la definición del vector producto de vectores a y B | a xb | =| a | * | b | sen g, es decir, S pares = | a x b |. Y, por tanto, D S = 1/2 | a x b |.

Determinación del momento de fuerza relativo a un punto.

Deje que se aplique una fuerza en el punto A F = AB Déjalo ir O- algún punto en el espacio (ver Fig. 20).

Se sabe por la física que momento de fuerza F relativo al punto O se llama vector METRO, que pasa por el punto O y:

1) perpendicular al plano que pasa por los puntos O, A, B;

2) numéricamente igual al producto de la fuerza por hombro

3) forma un triplete recto con los vectores OA y AB.

Por lo tanto, M = OA x F.

Encontrar la velocidad lineal de rotación

Velocidad v punto M de un cuerpo rígido que gira con una velocidad angular w alrededor de un eje fijo, se determina mediante la fórmula de Euler v = w хr, donde r = ОМ, donde О es algún punto fijo del eje (ver Fig. 21).

Usando el producto vectorial de VECTORES

para calcular el área

algunas formas geométricas

Trabajo de investigación en matemáticas

Alumno 10 grado B

MOU SOSH №73

Perevoznikov Mikhail

Líderes:

Maestra de matemáticas MOU escuela secundaria No. 73 Dragunova Svetlana Nikolaevna

Asistente del Departamento análisis matemático de la Facultad de Mecánica y Matemáticas de SSU que lleva el nombre N.G. Chernyshevsky Berdnikov Gleb Sergeevich

Saratov, 2015

Introducción.

1. Revisión teórica.

1.1. Vectores y cálculos con vectores.

1.2. Usar el producto escalar de los vectores en la resolución de problemas

1.3 Producto escalar de vectores en coordenadas

1.4. Producto vectorial de vectores en el espacio euclidiano tridimensional: definición del concepto.

1.5. Coordenadas vectoriales productos de vectores.

2. La parte práctica.

2.1. Relación del producto vectorial con el área de un triángulo y un paralelogramo. Derivación de la fórmula y el significado geométrico del vector producto de vectores.

2.2. Conociendo solo las coordenadas de los puntos, calcula el área del triángulo. Prueba del teorema

2.3. Comprobación de la exactitud de la fórmula mediante ejemplos.

2.4. Uso práctico de álgebra vectorial y producto vectorial.

Conclusión

Introducción

Como sabe, muchos problemas geométricos tienen dos formas clave de resolución: gráfica y analítica. El método gráfico está asociado con la construcción de gráficos y dibujos, y el método analítico implica la resolución de problemas utilizando principalmente acciones algebraicas. En el último caso, el algoritmo de resolución de problemas está asociado a la geometría analítica. La geometría analítica es un campo de las matemáticas, o más bien del álgebra lineal, que considera la solución de problemas geométricos mediante el álgebra basada en el método de coordenadas en un plano y en el espacio. La geometría analítica le permite analizar imágenes geométricas, líneas y superficies que son importantes para aplicaciones prácticas. Además, en esta ciencia, para ampliar la comprensión espacial de las figuras, además, a veces se utiliza el producto vectorial de los vectores.

Debido al uso generalizado de tecnologías espaciales tridimensionales, el estudio de las propiedades de algunas figuras geométricas utilizando un producto vectorial parece ser relevante.

Al respecto, se indicó el objetivo de este proyecto: el uso del producto vectorial de vectores para calcular el área de algunas formas geométricas.

En relación con este objetivo, se resolvieron las siguientes tareas:

1. Estudiar teóricamente los fundamentos necesarios del álgebra vectorial y definir el producto vectorial de los vectores en un sistema de coordenadas;

2. Analizar la conexión entre el producto vectorial y el área del triángulo y el paralelogramo;

3. Derive la fórmula para el área de un triángulo y un paralelogramo en coordenadas;

4. Verifique en ejemplos específicos la exactitud de la fórmula derivada.

1. Revisión teórica.

Un vector es un segmento dirigido, para el cual se indican su inicio y final:

En este caso, el comienzo del segmento es el punto A, el final del segmento es el punto V... El vector en sí se denota por
o ... Para encontrar las coordenadas de un vector
, conociendo las coordenadas de su punto inicial A y punto final B, es necesario restar las coordenadas correspondientes del punto inicial de las coordenadas del punto final:

= { B X - A X ; B y - A y }

Los vectores colineales son vectores que se encuentran en líneas paralelas o en una línea recta. En este caso, el vector es un segmento caracterizado por longitud y dirección.

La longitud del segmento direccional determina el valor numérico del vector y se denomina longitud del vector o módulo del vector.

Longitud del vector || en coordenadas cartesianas rectangulares es igual a la raíz cuadrada de la suma de los cuadrados de sus coordenadas.

Puede realizar varias acciones con vectores.

Por ejemplo, suma. Para agregarlos, primero debe dibujar el segundo vector desde el final del primero y luego conectar el comienzo del primero al final del segundo (Fig. 1). La suma de los vectores es otro vector con nuevas coordenadas.

Suma de vectores = {a X ; a y) y = {B X ; B y) se puede encontrar utilizando la siguiente fórmula:

+ = (un X + b X ; a y + b y }

Arroz. 1. Acciones con vectores

Restando vectores, primero debes dibujarlos de un punto y luego conectar el final del segundo con el final del primero.

Vectores de diferencia = {a X ; a y) y = {B X ; B y } se puede encontrar mediante la fórmula:

- = { a X - B X ; a y - B y }

Además, los vectores se pueden multiplicar por un número. El resultado también será un vector k veces más grande (o más pequeño) que el dado. Su dirección dependerá del signo de k: para k positivo, los vectores están codirigidos y para negativos, opuestos.

Producto de un vector = {a X ; a y } y los números k se pueden encontrar usando la siguiente fórmula:

k = (k A X ; k a y }

¿Es posible multiplicar un vector por un vector? Por supuesto, ¡e incluso dos opciones!

La primera opción es el producto escalar.

Arroz. 2. Producto escalar en coordenadas

Para encontrar el producto de los vectores, puede usar el ángulo  entre estos vectores, que se muestra en la Figura 3.

De la fórmula se deduce que el producto escalar es igual al producto de las longitudes de estos vectores por el coseno del ángulo entre ellos, su resultado es un número. Es importante que si los vectores son perpendiculares, entonces su producto escalar es igual a cero, porque el coseno del ángulo recto entre ellos es cero.

En el plano de coordenadas, el vector también tiene coordenadas. V Los vectores, sus coordenadas y el producto escalar son algunos de los métodos más convenientes para calcular el ángulo entre líneas rectas (o sus segmentos de línea) si se ingresa un sistema de coordenadas.Y si las coordenadas
, entonces su producto escalar es igual a:

En el espacio tridimensional, hay 3 ejes y, en consecuencia, los puntos y vectores en dicho sistema tendrán 3 coordenadas, y el producto escalar de los vectores se calcula mediante la fórmula:

1.2. Producto vectorial de vectores en espacio tridimensional.

La segunda opción para calcular el producto de vectores es el producto cruzado. Pero para definirlo ya no se requiere un plano, sino un espacio tridimensional, en el que el principio y el final del vector tienen 3 coordenadas.

En contraste con el producto escalar de vectores en el espacio tridimensional, la operación de "multiplicación de vectores" sobre vectores conduce a un resultado diferente. Si en el caso anterior de la multiplicación escalar de dos vectores el resultado fue un número, entonces en el caso de la multiplicación vectorial de vectores el resultado será otro vector perpendicular a ambos vectores entrando en el producto. Por lo tanto, este producto de vectores se denomina producto vectorial.

Obviamente, al construir el vector resultante , perpendicular a los dos que entraron en la obra - y, se pueden elegir dos direcciones opuestas. En este caso, la dirección del vector resultante está determinada por la regla de la mano derecha, o la regla del cardán. Si dibujamos vectores de modo que sus orígenes coincidan y rotamos el primer factor vectorial de la forma más corta posible al segundo factor vectorial, y cuatro dedos del La mano derecha mostró la dirección de rotación (como si cubriera un cilindro giratorio), luego el pulgar que sobresale mostrará la dirección del vector del producto (fig. 7).

Arroz. 7. Regla de la mano derecha

1.3. Propiedades del producto vectorial de vectores.

La longitud del vector resultante está determinada por la fórmula

Donde
producto cruzado. Como se mencionó anteriormente, el vector resultante será perpendicular
, y su dirección está determinada por la regla de la mano derecha.

El producto vectorial depende del orden de los factores, a saber:

El producto cruzado de vectores distintos de cero es 0, si son colineales, entonces el seno del ángulo entre ellos será 0.

Las coordenadas de los vectores en el espacio tridimensional se expresan de la siguiente manera: Luego, las coordenadas del vector resultante se encuentran mediante la fórmula

La longitud del vector resultante se encuentra mediante la fórmula:

2. La parte práctica.

2.1. Relación del producto vectorial con el área de un triángulo y un paralelogramo en un plano. El significado geométrico del producto vectorial de vectores.

Démosle un triángulo ABC (Fig. 8). Se sabe que .

Si representamos los lados del triángulo AB y AC en forma de dos vectores, entonces en la fórmula para el área del triángulo encontramos la expresión del producto vectorial de vectores:

A partir de lo anterior, puede determinar el significado geométrico del producto vectorial (Fig.9):

la longitud del producto vectorial de vectores es igual al área duplicada de un triángulo que tiene vectores y lados, si se apartan de un punto.

En otras palabras, la longitud del vector producto de vectores y es igual al área del paralelogramo,construido en vectores y , con lados y y el ángulo entre ellos, igual.

Arroz. 9. El significado geométrico del producto vectorial de vectores.

En este sentido, podemos dar una definición más del producto vectorial de vectores. :

Producto de vector de vector en un vector se llama vector , cuya longitud es numéricamente igual al área del paralelogramo construido sobre los vectores y, perpendicular al plano de estos vectores y dirigido de modo que la mínima rotación desde k alrededor del vector se llevó a cabo en sentido antihorario, visto desde el final del vector (Fig. 10).

Arroz. 10. Determinación del producto vectorial de vectores.

usando un paralelogramo

2.2. Derivación de la fórmula para encontrar el área de un triángulo en coordenadas.

Entonces, se nos da un triángulo ABC en el plano y las coordenadas de sus vértices. Encontremos el área de este triángulo (fig. 11).

Arroz. 11. Un ejemplo de cómo resolver el problema de encontrar el área de un triángulo por las coordenadas de sus vértices.

Solución.

Para empezar, considere las coordenadas de los vértices en el espacio y calcule las coordenadas de los vectores AB y AC.

Usando la fórmula dada arriba, calculamos las coordenadas de su producto cruzado. La longitud de este vector es igual a 2 áreas del triángulo ABC. El área del triángulo es 10.

Además, si consideramos un triángulo en el plano, entonces las 2 primeras coordenadas del producto vectorial siempre serán cero, por lo que podemos formular el siguiente teorema.

Teorema: Sea un triángulo ABC y las coordenadas de sus vértices (Fig. 12).

Luego .

Arroz. 12. Prueba del teorema

Prueba.

Considere puntos en el espacio y calcule las coordenadas de los vectores BC y VA. ... Usando la fórmula dada anteriormente, calculamos las coordenadas del producto vectorial de estos vectores. Tenga en cuenta que todos los términos que contienenz 1 o z 2 son iguales a 0, porque z 1 y z 2 = 0. QUITAR !!!

Asi que, por lo tanto

2.3. Comprobación de la exactitud de la fórmula mediante ejemplos

Encuentra el área de un triángulo formado por vectores a = (-1; 2; -2) yb = (2; 1; -1).

Solución: Encontremos el producto cruzado de estos vectores:

a × b =

Yo (2 (-1) - (-2) 1) - j ((- 1) (-1) - (-2) 2) + k ((- 1) 1-2 2) =

Yo (-2 + 2) - j (1 + 4) + k (-1 - 4) = -5 j - 5 k = (0; -5; -5)

De las propiedades del producto vectorial:

SΔ =

| a × b | =

√ 02 + 52 + 52 =

√ 25 + 25 =

√ 50 =

5√ 2

Respuesta: SΔ = 2.5√2.

Conclusión

2.4. Aplicaciones de álgebra vectorial

y producto escalar y vectorial de vectores.

¿Dónde se necesitan los vectores? El espacio vectorial y los vectores no solo son teóricos, sino que también tienen una aplicación práctica muy real en el mundo moderno.

En mecánica y física, muchas cantidades no solo tienen un valor numérico, sino también una dirección. Estas cantidades se denominan vector. Junto al uso de conceptos mecánicos elementales, en función de su significado físico, muchas cantidades se consideran vectores deslizantes, y sus propiedades se describen tanto mediante axiomas, como es habitual en la mecánica teórica, como mediante las propiedades matemáticas de los vectores. Los ejemplos más llamativos de cantidades vectoriales son la velocidad, el momento y la fuerza (Fig. 12). Por ejemplo, el momento angular y la fuerza de Lorentz se escriben matemáticamente usando vectores.

En física, no solo los vectores en sí son importantes, sino que también lo son sus productos, que ayudan a calcular ciertas cantidades. El producto vectorial es útil para determinar la colinealidad de los vectores, el módulo del producto vectorial de dos vectores es igual al producto de sus módulos si son perpendiculares y disminuye a cero si los vectores están codirigidos o son opuestos.

Otro ejemplo: el producto escalar se usa para calcular el trabajo usando la fórmula siguiente, donde F es el vector de fuerza y s es el vector de desplazamiento.

Un ejemplo de uso del producto de vectores es el momento de fuerza igual al producto del vector de radio dibujado desde el eje de rotación hasta el punto de aplicación de la fuerza por el vector de esta fuerza.

Gran parte de lo que se calcula en física de acuerdo con la regla de la mano derecha es un producto vectorial. Encuentra confirmación, da ejemplos.

También vale la pena señalar que el espacio bidimensional y tridimensional no agota las posibles variantes de los espacios vectoriales. Las matemáticas superiores consideran espacios de dimensión superior, en los que también se definen análogos de fórmulas para productos escalares y vectoriales. A pesar de que los espacios de mayor dimensión que 3, la conciencia humana es incapaz de representar visualmente, sorprendentemente encuentran aplicaciones en muchas áreas de la ciencia y la industria.

Al mismo tiempo, el resultado del vector producto de vectores en el espacio euclidiano tridimensional no es un número, sino el vector resultante con sus coordenadas, dirección y longitud.

La dirección del vector resultante está determinada por la regla de la mano derecha, que es uno de los puntos más sorprendentes de la geometría analítica.

El producto vectorial de vectores se puede usar para encontrar el área de un triángulo o paralelogramo para las coordenadas dadas de los vértices, lo cual se confirmó al derivar una fórmula, probar un teorema y resolver problemas prácticos.

Los vectores se utilizan ampliamente en física, donde indicadores como la velocidad, el momento y la fuerza se pueden representar como cantidades vectoriales y se calculan geométricamente.

Lista de fuentes utilizadas

Atanasyan L.S., Butuzov V.F., Kadomtsev S. B. et al. Geometry. 7-9 grados: un libro de texto para organizaciones educativas. M .:, 2013.383 pág.

Atanasyan L.S., Butuzov V.F., Kadomtsev S. B. et al. Geometry. 10-11 grados: un libro de texto para organizaciones educativas: niveles básico y de perfil. M .:, 2013.255 s.

Bugrov Y.S., Nikolsky S.M. Matemáticas avanzadas. Volumen uno: Elementos de álgebra lineal y geometría analítica.

D. V. Kletenik Colección de problemas en geometría analítica. Moscú: Nauka, Fizmatlit, 1998.

Geometría analítica.

Matemáticas. Trébol.

Aprenda matemáticas en línea.

http://ru.onlinemschool.com/math/library/vector/multiply1/

Sitio web de V. Glaznev.

http://glaznev.sibcity.ru/1kurs/analit/common/html/anlek7.htm

Wikipedia.

https://ru.wikipedia.org/wiki/%C2%E5%EA%F2%EE%F0%ED%EE%E5_%EF%F0%EE%E8%E7%E2%E5%E4%E5%ED % E8% E5