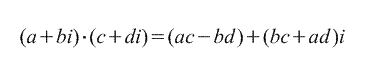
Représentation d'un nombre complexe sous forme trigonométrique. Multiplication de nombres complexes. Question. Plan complexe. Module et arguments des nombres complexes
Le produit de deux nombres complexes est semblable au produit de deux nombres réels, à savoir : le produit est considéré comme un nombre constitué d'un multiplicande, tout comme un facteur est constitué d'une unité. Le vecteur correspondant à un nombre complexe de module r et d'argument j peut être obtenu à partir de vecteur unitaire, dont la longueur est égale à l'unité et dont la direction coïncide avec la direction positive de l'axe OX, en l'allongeant r fois et en le faisant tourner dans le sens positif d'un angle j. Le produit d'un certain vecteur a 1 par un vecteur a 2 est le vecteur obtenu si l'on applique un allongement et une rotation au vecteur a 1, à l'aide duquel le vecteur a 2 est obtenu à partir d'un vecteur unitaire, et ce dernier correspond évidemment à une unité réelle. Si (r 1 , ? 1), (r 2 , ? 2) sont les modules et arguments de nombres complexes correspondant aux vecteurs a 1 et a 2, alors le produit de ces vecteurs correspondra évidemment à un nombre complexe de module r 1 r 2 et argument (j 1 + j 2). Ainsi, le produit de deux nombres complexes est un nombre complexe dont le module est égal au produit des modules des facteurs et dont l'argument est égal à la somme des arguments des facteurs.
Dans le cas où les nombres complexes sont écrits forme trigonométrique, aura
r 1 (cos ? 1 + je péché ? 1) * r 2 (cos ? 2 + je péché ? 2) = r 1 r 2.
Dans le cas (a 1 + b 1 i)(a 2 + b 2 i) = x + yi, en utilisant la notation des modules et des arguments des facteurs, on peut écrire :
une 1 = r 1 cos ? 1 ; b 1 = r 1 péché ? 1 ; une 2 = r 2 cos ? 2 ; b 2 = r 2 péché ? 2 ;
selon la définition de la multiplication :
x = r 1 r 2 cos(? 1 + ? 2); y = r 1 r 2 péché(? 1 + ? 2),
x = r 1 r 2 (cos ? 1 cos ? 2 - péché ? 1 péché ? 2) = = r 1 cos ? 1 r 2 parce que ? 2 - r 1 péché ? 1 r 2 péché ? 2 = une 1 une 2 - b 1 b 2
y = r 1 r 2 (péché ? 1 cos ? 2 + cos ? 1 péché ? 2) = = r 1 péché ? 1 r 2 parce que ? 2 + r 1 parce que ? 1 r 2 péché ? 2 = b 1 une 2 + une 1 b 2,
et finalement on obtient :
(une 1 + b 1 je)(une 2 + b 2 je) = (une 1 une 2 - b 1 b 2) + (b 1 une 2 + une 1 b 2)je.
Dans le cas b 1 = b 2 = 0, les facteurs sont des nombres réels a 1 et a 2 et le produit se réduit au produit a 1 a 2 de ces nombres. Quand
une 1 = une 2 = 0 et b 1 = b 2 = 1,
égalité (a 1 + b 1 i)(a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (b 1 a 2 + a 1 b 2)I donne : i???i = je 2 = -1, c'est-à-dire le carré de l'unité imaginaire est -1. En calculant séquentiellement les puissances entières positives i, on obtient :
je 2 = -1 ; je 3 = -je; je 4 = 1; je 5 = je; je 6 = -1; ...
et, en général, pour tout k positif :
je 4k = 1 ; je 4k+1 = je; je 4k+2 = -1 ; je 4k+3 = -je
La règle de multiplication exprimée par l'égalité (a 1 + b 1 i)(a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (b 1 a 2 + a 1 b 2)I peut être formulé comme suit : les nombres complexes doivent être multipliés comme des polynômes alphabétiques, en comptant i 2 = -1.
Des formules ci-dessus, il résulte immédiatement que l'addition et la multiplication de nombres complexes obéissent à la loi commutative, c'est-à-dire la somme ne dépend pas de l'ordre des termes, et le produit ne dépend pas de l'ordre des facteurs. Il n'est pas difficile de vérifier la validité des lois combinatoires et distributives, exprimées par les identités suivantes :
(? 1 + ? 2) + ? 3 = ? 1 + (? 2 + ? 3); (? 1 ? 2)? 3 = ? 1 (? 2 ? 3); (? 1 + ? 2)? = ? 1 ? + ? 2 ? .
Le produit de plusieurs facteurs aura un module égal au produit des modules des facteurs, et un argument égal à la somme des arguments des facteurs. Ainsi, le produit de nombres complexes sera égal à zéro si et seulement si au moins un des facteurs est égal à zéro.
Exemple : étant donnés les nombres complexes z 1 = 2 + 3i, z 2 = 5 - 7i. Trouver:
a) z 1 + z 2 ; b) z 1 - z 2 ; c) z 1 z 2 .
a) z 1 + z 2 = (2 + 3i) + (5 - 7i) = 2 + 3i + 5 - 7i = (2 + 5) + (3i - 7i) = 7 - 4i ; b) z 1 - z 2 = (2 + 3i) - (5 - 7i) = 2 + 3i - 5 + 7i = (2 - 5) + (3i + 7i) = - 3 + 10i ; c) z 1 z 2 = (2 + 3i)(5 - 7i) = 10 - 17i + 15i - 21i 2 = 10 - 14i + 15i + 21 = (10 + 21) + (- 14i + 15i) = 31 + je (ici on prend en compte que je 2 = - 1).
Exemple : suivez ces étapes :
une) (2 + 3i) 2 ; b) (3-5i) 2 ; c) (5 + 3i) 3 .
a) (2 + 3i) 2 = 4 + 2Х2Ч3i + 9i 2 = 4 + 12i - 9 = - 5 + 12i ; b) (3 - 5i) 2 = 9 - 2Х3Ч5i + 25i 2 = 9 - 30i - 25 = - 16 - 30i ; c) (5 + 3i) 3 = 125 + 3Х25Ч3i + 3Ч5Ч9i 2 + 27i 3 ; puisque i 2 = - 1, et i 3 = - i, nous obtenons (5 + 3i) 3 = 125 + 225i - 135 - - 27i = - 10 + 198i.
Exemple : effectuer des actions
une) (5 + 3i)(5 - 3i); b) (2 + 5i)(2 - 5i); c) (1 + je)(1 - je).
a) (5 + 3i)(5 - 3i) = 5 2 - (3i) 2 = 25 - 9i 2 = 25 + 9 = 34 ; b) (2 + 5i)(2 - 5i) = 2 2 - (5i) 2 = 4 + 25 = 29 ; c) (1 + je)(1 - je) = 1 2 - je 2 = 1 + 1 = 2.
Les nombres complexes sont l’extension minimale de l’ensemble des nombres réels que nous connaissons. Leur différence fondamentale est qu'un élément apparaît qui, lorsqu'il est au carré, donne -1, c'est-à-dire je, ou .
Tout nombre complexe se compose de deux parties : réel et imaginaire:
Ainsi, il est clair que l’ensemble des nombres réels coïncide avec l’ensemble des nombres complexes ayant une partie imaginaire nulle.
Le modèle le plus populaire pour l’ensemble des nombres complexes est le plan ordinaire. La première coordonnée de chaque point sera sa partie réelle, et la seconde sa partie imaginaire. Ensuite, le rôle des nombres complexes eux-mêmes sera celui de vecteurs commençant au point (0,0).
Opérations sur les nombres complexes.
En effet, si l'on prend en compte le modèle de l'ensemble des nombres complexes, il est intuitivement clair que l'addition (soustraction) et la multiplication de deux nombres complexes s'effectuent de la même manière que les opérations correspondantes sur les vecteurs. Et cela signifie produit vectoriel vecteurs, car le résultat de cette opération est à nouveau un vecteur.
1.1 Ajout.
(Comme vu, cette opération correspond exactement)
1.2 Soustraction, de même, est produit selon la règle suivante :
2. Multiplications.
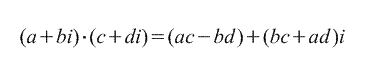
3. Division.
Défini simplement comme opération inverseà la multiplication.

Forme trigonométrique.
Le module d'un nombre complexe z est la quantité suivante :
 ,
,
évidemment, il ne s'agit, encore une fois, que du module (longueur) du vecteur (a,b).
Le plus souvent, le module d'un nombre complexe est noté ρ.
Il se trouve que
z = ρ(cosφ+isinφ).

Ce qui suit découle directement de la forme trigonométrique d’écriture d’un nombre complexe : formules :

La dernière formule s'appelle La formule de Moivre. La formule en dérive directement racine nième d'un nombre complexe:

ainsi, il y a n nièmes racines du nombre complexe z.
Un nombre complexe est un nombre de la forme , où et sont des nombres réels, appelés unité imaginaire. Le numéro est appelé partie réelle() nombre complexe, le nombre s'appelle partie imaginaire () nombre complexe.
Les nombres complexes sont représentés par plan complexe:

Comme mentionné ci-dessus, une lettre désigne généralement un ensemble de nombres réels. Un tas de même nombres complexes généralement désigné par une lettre « gras » ou épaissie. Par conséquent, la lettre doit être placée sur le dessin, indiquant que nous avons un plan complexe.
Forme algébrique d'un nombre complexe. Addition, soustraction, multiplication et division de nombres complexes
Ajout de nombres complexes
Pour additionner deux nombres complexes, vous devez additionner leurs parties réelle et imaginaire :
z 1 + z 2 = (une 1 + une 2) + je*(b 1 + b 2).
Pour les nombres complexes, la règle de la première classe est valable : z 1 + z 2 = z 2 + z 1 – la somme ne change pas en réorganisant les termes.
Soustraire des nombres complexes
L'action est similaire à l'addition, la seule particularité est que le sous-trahend doit être mis entre parenthèses, puis les parenthèses doivent être ouvertes de la manière standard avec un changement de signe :
z 1 + z 2 = (une 1 – une 2) + je*(b 1 – b 2)
Multiplier des nombres complexes
Égalité fondamentale des nombres complexes :
Produit de nombres complexes :
z 1 * z 2 = (a 1 + i*b 1)*(a 2 + i*b 2) = a 1 *a 2 + a 1 *i*b 2 + a 2 *i*b 1 + i 2 *b 1 *b 2 = a 1 *a 2 - b 1 *b 2 +i*(a 1 *b 2 +a 2 *b 1).
Comme la somme, le produit de nombres complexes est commutable, c'est-à-dire que l'égalité est vraie : .
Division de nombres complexes
La division des nombres s'effectue en multipliant le dénominateur et le numérateur par l'expression conjuguée du dénominateur.
2 Question. Plan complexe. Module et arguments des nombres complexes
Chaque nombre complexe z = a + i*b peut être associé à un point de coordonnées (a;b), et vice versa, chaque point de coordonnées (c;d) peut être associé à un nombre complexe w = c + i* d. Ainsi, une correspondance biunivoque s'établit entre les points du plan et l'ensemble des nombres complexes. Les nombres complexes peuvent donc être représentés comme des points sur un plan. Le plan sur lequel les nombres complexes sont représentés est généralement appelé plan complexe.

Cependant, le plus souvent, les nombres complexes sont représentés comme un vecteur commençant au point O, à savoir, le nombre complexe z = a + i*b est représenté comme un rayon vecteur d'un point de coordonnées (a;b). Dans ce cas, l'image des nombres complexes de l'exemple précédent ressemblera à ceci : 
L'image de la somme de deux nombres complexes est un vecteur égal à la somme des vecteurs représentant les nombres et . En d’autres termes, lorsque des nombres complexes sont ajoutés, les vecteurs qui les représentent sont également ajoutés.

Soit le nombre complexe z = a + i*b représenté par un rayon vecteur. Alors la longueur de ce vecteur s’appelle module numéro z et est noté |z| .
|
|

L'angle formé par le rayon vecteur d'un nombre avec l'axe s'appelle argument nombres et est noté arg z. L'argument du nombre n'est pas déterminé de manière unique, mais à un multiple près de . Cependant, l'argument est généralement spécifié dans la plage de 0 ou dans la plage de -à. De plus, number a un argument non défini.
En utilisant cette relation, vous pouvez trouver l'argument d'un nombre complexe :
De plus, la première formule est valable si l'image du nombre est au premier ou au quatrième quartier, et la seconde, si elle est au deuxième ou au troisième. Si , alors le nombre complexe est représenté par un vecteur sur l'axe Oy et son argument est égal à /2 ou 3*/2.
Prenons-en un autre formule utile. Soit z = a + i*b. Alors ,
On définit le produit de deux nombres complexes de la même manière que le produit de nombres réels, à savoir : le produit est considéré comme un nombre constitué d'un multiplicande, tout comme un facteur est constitué d'une unité.
Le vecteur correspondant à un nombre complexe avec module et argument peut être obtenu à partir d'un vecteur unitaire dont la longueur est égale à un et dont la direction coïncide avec la direction positive de l'axe OX, en l'allongeant d'un facteur et en le faisant tourner dans le sens positif d'un angle
Le produit d'un certain vecteur par un vecteur est le vecteur qui sera obtenu si l'on applique au vecteur l'allongement et la rotation mentionnés ci-dessus, à l'aide desquels le vecteur est obtenu à partir d'un vecteur unitaire, et ce dernier correspond évidemment à une véritable unité.
Si les modules et arguments sont des nombres complexes correspondant à des vecteurs, alors le produit de ces vecteurs correspondra évidemment à un nombre complexe de module et d'argument . On arrive ainsi à la définition suivante du produit de nombres complexes :
Le produit de deux nombres complexes est un nombre complexe dont le module est égal au produit des modules des facteurs et dont l'argument est égal à la somme des arguments des facteurs.
Ainsi, dans le cas où les nombres complexes sont écrits sous forme trigonométrique, on aura
Dérivons maintenant la règle de composition d'un produit pour le cas où les nombres complexes ne sont pas donnés sous forme trigonométrique :
En utilisant la notation ci-dessus pour les modules et les arguments des facteurs, nous pouvons écrire
selon la définition de la multiplication (6) :

et finalement nous obtenons
Dans le cas où les facteurs sont des nombres réels et le produit est réduit au produit aag de ces nombres. Dans le cas d'égalité (7) donne
![]()
c'est-à-dire que le carré de l'unité imaginaire est égal à
En calculant séquentiellement les puissances entières positives, on obtient
et en général, avec tout positif global
La règle de multiplication exprimée par l'égalité (7) peut être formulée ainsi : les nombres complexes doivent être multipliés comme les polynômes de lettres, en comptant
Si a est un nombre complexe, alors le nombre complexe est dit conjugué à a et est noté a. D'après les formules (3) on a de l'égalité (7) il s'ensuit
et par conséquent,
c'est-à-dire que le produit des nombres complexes conjugués est égal au carré du module de chacun d'eux.
Notons aussi des formules évidentes
Des formules (4) et (7), il résulte immédiatement que l'addition et la multiplication de nombres complexes obéissent à la loi commutative, c'est-à-dire que la somme ne dépend pas de l'ordre des termes, et le produit ne dépend pas de l'ordre des facteurs. Il n'est pas difficile de vérifier la validité des lois combinatoires et distributives, exprimées par les identités suivantes :
Nous laissons le soin au lecteur de le faire.
Notons enfin que le produit de plusieurs facteurs aura un module égal au produit des modules des facteurs, et un argument égal à la somme des arguments des facteurs. Ainsi, le produit de nombres complexes sera égal à zéro si et seulement si au moins un des facteurs est égal à zéro.
