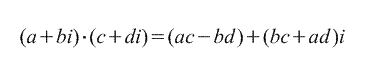
Znázornenie komplexného čísla v trigonometrickom tvare. Násobenie komplexných čísel. Otázka. Komplexná rovina. Modul a argumenty komplexných čísel
Súčin dvoch komplexných čísel je podobný súčinu dvoch reálnych čísel, a to: súčin sa považuje za číslo zložené z násobku, rovnako ako činiteľ sa skladá z jednotky. Vektor zodpovedajúci komplexnému číslu s modulom r a argumentom j možno získať z jednotkový vektor, ktorej dĺžka sa rovná jednotke a ktorej smer sa zhoduje s kladným smerom osi OX, a to jej predĺžením r-krát a otočením v kladnom smere o uhol j. Súčin určitého vektora a 1 s vektorom a 2 je vektor, ktorý získame, ak na vektor a 1 aplikujeme predĺženie a rotáciu, pomocou ktorej sa vektor a 2 získa z jednotkového vektora a ten zjavne zodpovedá skutočnej jednotke. Ak (r 1 , ? 1), (r 2 , ? 2) sú moduly a argumenty komplexných čísel zodpovedajúcich vektorom a 1 a a 2, potom súčin týchto vektorov bude zjavne zodpovedať komplexnému číslu s modulom r 1 r 2 a argument (j 1 + j 2). Súčin dvoch komplexných čísel je teda komplexné číslo, ktorého modul sa rovná súčinu modulov faktorov a ktorého argument sa rovná súčtu argumentov faktorov.
V prípade, že sú zapísané komplexné čísla trigonometrická forma, bude mať
r 1 (cos? 1 + i hriech? 1) * r 2 (cos? 2 + i hriech? 2) = r 1 r 2.
V prípade (a 1 + b 1 i)(a 2 + b 2 i) = x + yi pomocou zápisu modulov a argumentov faktorov môžeme napísať:
a 1 = r 1 cos? 1; b 1 = r 1 hriech? 1; a 2 = r 2 čos? 2; b 2 = r 2 hriech? 2;
podľa definície násobenia:
x = r1r2cos(a 1 + > 2); y = r 1 r 2 sin(? 1 + ? 2),
x = r 1 r 2 (cos? 1 cos? 2 - hriech? 1 hriech? 2) = = r 1 cos? 1 r 2 čo? 2 - r 1 hriech? 1 r 2 hriech? 2 = a 1 a 2 - b 1 b 2
y = r 1 r 2 (hriech? 1 cos? 2 + cos? 1 hriech? 2) = = r 1 hriech? 1 r 2 čo? 2 + r 1 čo? 1 r 2 hriech? 2 = b 1 a 2 + a 1 b 2,
a nakoniec dostaneme:
(a 1 + b 1 i) (a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (b 1 a 2 + a 1 b 2)i.
V prípade b 1 = b 2 = 0 sú činiteľmi reálne čísla a 1 a a 2 a súčin sa redukuje na súčin a 1 a 2 týchto čísel. Kedy
a 1 = a 2 = 0 a b 1 = b 2 = 1,
rovnosť (a 1 + b 1 i)(a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (b 1 a 2 + a 1 b 2)I dáva: i???i = i2 = -1, t.j. druhá mocnina imaginárnej jednotky je -1. Postupným výpočtom kladných celých mocnín i dostaneme:
i2 = -1; i3 = -i; i4 = 1; i5 = i; i6 = -1; ...
a vo všeobecnosti pre každé kladné k:
i4k = 1; i4k+1 = i; i4k+2 = -1; i 4k+3 = -i
Pravidlo násobenia vyjadrené rovnosťou (a 1 + b 1 i)(a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (b 1 a 2 + a 1 b 2)I môže byť formulované takto: komplexné čísla sa musia násobiť ako abecedné polynómy, pričom sa počíta i 2 = -1.
Z vyššie uvedených vzorcov okamžite vyplýva, že sčítanie a násobenie komplexných čísel sa riadi komutatívnym zákonom, t.j. súčet nezávisí od poradia výrazov a súčin nezávisí od poradia faktorov. Nie je ťažké overiť platnosť kombinačných a distributívnych zákonov, vyjadrených nasledujúcimi identitami:
(? 1 + ? 2) + ? 3 = ? 1 + (? 2 + ? 3); (? 1 ? 2)? 3 = ? 1 (? 2 ? 3); (? 1 + ? 2)? = ? 1 ? + ? 2 ? .
Súčin niekoľkých faktorov bude mať modul rovný súčinu modulov faktorov a argument rovný súčtu argumentov faktorov. Súčin komplexných čísel sa teda bude rovnať nule vtedy a len vtedy, ak sa aspoň jeden z faktorov rovná nule.
Príklad: dané komplexné čísla z 1 = 2 + 3i, z 2 = 5 - 7i. Nájsť:
a) zi + z2; b) zi - z2; c) z 1 z 2 .
a) zi + z2 = (2 + 3i) + (5 - 7i) = 2 + 3i + 5 - 7i = (2 + 5) + (3i - 7i) = 7 - 4i; b) zi - z2 = (2 + 3i) - (5 - 7i) = 2 + 3i - 5 + 7i = (2 - 5) + (3i + 7i) = - 3 + 10i; c) z 1 z 2 = (2 + 3i) (5 - 7i) = 10 - 17i + 15i - 21i 2 = 10 - 14i + 15i + 21 = (10 + 21) + (- 14i + 15i) = 31 + i (tu sa berie do úvahy, že i 2 = - 1).
Príklad: postupujte podľa týchto krokov:
a) (2 + 3i)2; b) (3-5i)2; c) (5 + 3i)3.
a) (2 + 3i) 2 = 4 + 2H203i + 9i 2 = 4 + 12i - 9 = - 5 + 12i; b) (3 - 5i) 2 = 9 - 2H305i + 25i 2 = 9 - 30i - 25 = -16 - 30i; c) (5 + 3i)3 = 125 + 3Х25Ч3i + 3Ч5Ч9i2 + 27i3; keďže i 2 = - 1 a i 3 = - i, dostaneme (5 + 3i) 3 = 125 + 225i - 135 - - 27i = - 10 + 198i.
Príklad: vykonávať akcie
a) (5 + 3i) (5 - 3i); b) (2 + 5i) (2 - 5i); c) (1 + i) (1 - i).
a) (5 + 3i) (5 - 3i) = 52 - (3i)2 = 25 - 9i 2 = 25 + 9 = 34; b) (2 + 5i) (2 - 5i) = 22 - (5i)2 = 4 + 25 = 29; c) (1 + i) (1 - i) = 12 - i2 = 1 + 1 = 2.
Komplexné čísla sú minimálnym rozšírením množiny reálnych čísel, ktoré poznáme. ich zásadný rozdiel je, že sa objaví prvok, ktorý pri odmocnení dáva -1, t.j. ja alebo .
Každé komplexné číslo sa skladá z dvoch častí: skutočné a vymyslené:
Je teda zrejmé, že množina reálnych čísel sa zhoduje s množinou komplexných čísel s nulovou imaginárnou časťou.
Najpopulárnejším modelom pre množinu komplexných čísel je obyčajná rovina. Prvá súradnica každého bodu bude jeho skutočnou časťou a druhá bude jeho imaginárnou časťou. Potom úlohou samotných komplexných čísel budú vektory so začiatkom v bode (0,0).
Operácie s komplexnými číslami.
V skutočnosti, ak vezmeme do úvahy model množiny komplexných čísel, je intuitívne jasné, že sčítanie (odčítanie) a násobenie dvoch komplexných čísel sa vykonáva rovnakým spôsobom ako zodpovedajúce operácie s vektormi. A toto znamená vektorový produkt vektory, pretože výsledkom tejto operácie je opäť vektor.
1.1 Doplnenie.
(Ako je vidieť, túto operáciu presne sa zhoduje)
1.2 Odčítanie, podobne sa vyrába podľa nasledujúceho pravidla:
2. Násobenie.
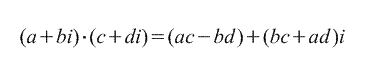
3. Rozdelenie.
Definované jednoducho ako spätný chod k množeniu.

Trigonometrická forma.
Modul komplexného čísla z je nasledujúca veličina:
 ,
,
samozrejme, toto je opäť len modul (dĺžka) vektora (a,b).
Najčastejšie sa modul komplexného čísla označuje ako ρ.
Ukazuje sa, že
z = ρ(cosφ+isinφ).

Priamo z trigonometrickej formy zápisu komplexného čísla vyplýva: vzorce :

Posledný vzorec je tzv Moivreov vzorec. Vzorec je odvodený priamo od neho n-tá odmocnina komplexného čísla:

teda existujú n-té korene komplexného čísla z.
Komplexné číslo je číslo tvaru , kde a sú reálne čísla, tzv pomyselná jednotka. Číslo sa volá skutočná časť () komplexné číslo, číslo sa volá imaginárnu časť () komplexné číslo.
Komplexné čísla sú reprezentované komplexná rovina:

Ako je uvedené vyššie, písmeno zvyčajne označuje množinu reálnych čísel. Kopa rovnaký komplexné čísla zvyčajne označené „tučným“ alebo zhrubnutým písmenom. Preto by malo byť písmeno umiestnené na výkrese, čo naznačuje skutočnosť, že máme zložitú rovinu.
Algebraický tvar komplexného čísla. Sčítanie, odčítanie, násobenie a delenie komplexných čísel
Sčítanie komplexných čísel
Ak chcete pridať dve komplexné čísla, musíte pridať ich skutočnú a imaginárnu časť:
zi + z2 = (ai + a2) + i*(b1 + b2).
Pre komplexné čísla platí pravidlo prvej triedy: z 1 + z 2 = z 2 + z 1 – súčet sa preskupením pojmov nemení.
Odčítanie komplexných čísel
Akcia je podobná ako pri sčítaní, jedinou zvláštnosťou je, že subtrahend musí byť uvedený v zátvorkách a potom musia byť zátvorky otvorené štandardným spôsobom so zmenou znamienka:
z 1 + z 2 = (a 1 – a 2) + i* (b 1 – b 2)
Násobenie komplexných čísel
Základná rovnosť komplexných čísel:
Súčin komplexných čísel:
z 1 * z 2 = (a 1 + i*b 1)*(a 2 + i*b 2) = a 1 *a 2 + a 1 *i*b 2 + a 2 *i*b 1 + i 2 *b1*b2 = a1*a2-b1*b2+i*(a1*b2+a2*b1).
Rovnako ako súčet, súčin komplexných čísel je zameniteľný, to znamená, že rovnosť platí: .
Delenie komplexných čísel
Rozdelenie čísel sa vykonáva vynásobením menovateľa a čitateľa konjugovaným vyjadrením menovateľa.
2 Otázka. Komplexná rovina. Modul a argumenty komplexných čísel
Každé komplexné číslo z = a + i*b môže byť spojené s bodom so súradnicami (a;b) a naopak, každý bod so súradnicami (c;d) môže byť spojený s komplexným číslom w = c + i* d. Takto sa vytvorí korešpondencia jedna ku jednej medzi bodmi roviny a množinou komplexných čísel. Preto môžu byť komplexné čísla reprezentované ako body v rovine. Rovina, na ktorej sú zobrazené komplexné čísla, sa zvyčajne nazýva komplexná rovina.

Častejšie sa však komplexné čísla zobrazujú ako vektor so začiatkom v bode O, konkrétne komplexné číslo z = a + i*b je znázornené ako vektor polomeru bodu so súradnicami (a;b). V tomto prípade bude obraz komplexných čísel z predchádzajúceho príkladu takýto: 
Obraz súčtu dvoch komplexných čísel je vektor rovný súčtu vektorov reprezentujúcich čísla a . Inými slovami, keď sa sčítajú komplexné čísla, pridajú sa aj vektory, ktoré ich reprezentujú.

Nech je komplexné číslo z = a + i*b reprezentované polomerovým vektorom. Potom sa nazýva dĺžka tohto vektora modulčíslo z a označuje sa |z| .
|
|

Uhol, ktorý zviera polomer vektora čísla s osou, sa nazýva argumentčísla a označuje sa arg z. Argument čísla nie je určený jednoznačne, ale v rámci násobku . Zvyčajne je však argument uvedený v rozsahu od 0 alebo v rozsahu od -do. Okrem toho má číslo nedefinovaný argument.
Pomocou tohto vzťahu môžete nájsť argument komplexného čísla:
Prvý vzorec je navyše platný, ak je obrázok čísla v prvej alebo štvrtej štvrtine, a druhý, ak je v druhej alebo tretej štvrtine. Ak , potom je komplexné číslo reprezentované vektorom na osi Oy a jeho argument sa rovná /2 alebo 3*/2.
Dajme si ďalšiu užitočný vzorec. Nech z = a + i*b. potom ,
Súčin dvoch komplexných čísel definujeme podobne ako súčin reálnych čísel, a to: súčin považujeme za číslo zložené z násobku, tak ako súčin tvorený jednotkou.
Vektor zodpovedajúci komplexnému číslu s modulom a argumentom možno získať z jednotkového vektora, ktorého dĺžka sa rovná jednej a ktorého smer sa zhoduje s kladným smerom osi OX, jeho predĺžením o faktor a otočením v kladnom smere o uhol
Súčin určitého vektora vektorom je vektor, ktorý sa získa, ak sa na vektor aplikuje vyššie uvedené predĺženie a rotácia, pomocou ktorej sa vektor získa z jednotkového vektora a ten zjavne zodpovedá skutočná jednotka.
Ak sú moduly a argumenty komplexné čísla zodpovedajúce vektorom, potom súčin týchto vektorov bude zjavne zodpovedať komplexnému číslu s modulom a argumentom . Dostávame sa teda k nasledujúcej definícii súčinu komplexných čísel:
Súčin dvoch komplexných čísel je komplexné číslo, ktorého modul sa rovná súčinu modulov faktorov a ktorého argument sa rovná súčtu argumentov faktorov.
Teda v prípade, keď sú komplexné čísla napísané v goniometrickom tvare, budeme mať
Odvoďme teraz pravidlo na skladanie súčinu pre prípad, keď komplexné čísla nie sú zadané v trigonometrickom tvare:
Pomocou vyššie uvedeného zápisu modulov a argumentov faktorov môžeme písať
podľa definície násobenia (6):

a nakoniec dostaneme
V prípade, že faktory sú reálne čísla a súčin sa redukuje na súčin aag týchto čísel. V prípade rovnosti (7) dáva
![]()
t.j. druhá mocnina imaginárnej jednotky sa rovná
Postupným výpočtom kladných celočíselných mocnín dostaneme
a vo všeobecnosti s akýmkoľvek celkovo pozitívnym
Pravidlo násobenia vyjadrené rovnosťou (7) možno formulovať takto: komplexné čísla sa musia násobiť ako písmenové polynómy, počítať
Ak a je komplexné číslo, potom sa o komplexnom čísle hovorí, že je konjugované s a, a označuje sa a. Podľa vzorcov (3) máme z rovnosti (7) to vyplýva
a následne,
to znamená, že súčin konjugovaných komplexných čísel sa rovná druhej mocnine modulu každého z nich.
Všimnime si tiež zrejmé vzorce
Zo vzorcov (4) a (7) okamžite vyplýva, že sčítanie a násobenie komplexných čísel sa riadi komutatívnym zákonom, to znamená, že súčet nezávisí od poradia členov a súčin nezávisí od poradia prvkov. faktory. Nie je ťažké overiť platnosť kombinačných a distributívnych zákonov, vyjadrených nasledujúcimi identitami:
Necháme na čitateľa, ako to urobí.
Všimnite si nakoniec, že súčin niekoľkých faktorov bude mať modul rovný súčinu modulov faktorov a argument rovný súčtu argumentov faktorov. Súčin komplexných čísel sa teda bude rovnať nule vtedy a len vtedy, ak sa aspoň jeden z faktorov rovná nule.
