
Le point est le point du maximum local. Extrema, plus grandes et plus petites valeurs de fonctions
Le changement d'une fonction à un certain point est défini comme la limite de l'incrément de fonction à l'incrément d'argument, qui tend vers zéro. Pour le trouver, utilisez le tableau des dérivées. Par exemple, la dérivée de la fonction y = x3 sera égale à y '= x2.
Mettre cette dérivée à zéro (dans ce cas, x2 = 0).
Trouver la valeur de la variable donnée. Ce seront les valeurs lorsque la dérivée donnée est égale à 0. Pour ce faire, substituez des chiffres arbitraires dans l'expression au lieu de x, auquel l'expression entière devient zéro. Par exemple:
2-2x2 = 0
(1-x) (1 + x) = 0
x1 = 1, x2 = -1
Tracez les valeurs obtenues sur la ligne de coordonnées et calculez le signe de la dérivée pour chacune des valeurs obtenues. Les points sont marqués sur la ligne de coordonnées, qui sont prises comme origine. Pour calculer la valeur dans les intervalles, substituez des valeurs arbitraires qui correspondent aux critères. Par exemple, pour la fonction précédente, jusqu'à -1, vous pouvez choisir une valeur de -2. De -1 à 1, vous pouvez choisir 0, et pour les valeurs supérieures à 1, choisissez 2. Remplacez ces nombres dans la dérivée et découvrez le signe de la dérivée. Dans ce cas, la dérivée avec x = -2 sera de -0,24, c'est-à-dire négatif et il y aura un signe moins sur cet intervalle. Si x = 0, alors la valeur sera égale à 2, et un signe est placé sur cet intervalle. Si x = 1, alors la dérivée sera également de -0,24 et moins est mis.
Si, en passant par un point sur la ligne de coordonnées, la dérivée change de signe de moins en plus, alors c'est le point minimum, et si de plus en moins, alors c'est le point maximum.
Vidéos connexes
Pour trouver la dérivée, il existe des services en ligne qui calculent les valeurs requises et affichent le résultat. Sur de tels sites, vous pouvez trouver un dérivé jusqu'au 5ème ordre.
Sources:
- Un des services de calcul des dérivés
- point de fonction maximal
Les points maximum d'une fonction, ainsi que les points minimum, sont appelés points extremum. À ces points, la fonction change de comportement. Les extrema sont déterminés à des intervalles numériques limités et sont toujours locaux.
Instructions
Le processus de recherche des extrema locaux s'appelle une fonction et est effectué en analysant les dérivées première et seconde de la fonction. Assurez-vous que la plage spécifiée de valeurs d'argument est des valeurs valides avant d'examiner. Par exemple, pour la fonction F = 1 / x, la valeur de l'argument x = 0 est invalide. Ou, pour la fonction Y = tg (x), l'argument ne peut pas avoir la valeur x = 90 °.
Assurez-vous que la fonction Y est dérivable sur l'ensemble du segment donné. Trouvez la dérivée première Y". Évidemment, avant d'atteindre le point de maximum local, la fonction augmente, et en passant par le maximum, la fonction devient décroissante. La dérivée première à sa manière sens physique caractérise le taux de changement de la fonction. Alors que la fonction augmente, le taux de ce processus est positif. En passant par le maximum local, la fonction commence à décroître et la vitesse du processus de changement de fonction devient négative. La transition du taux de variation de la fonction par zéro se produit au point du maximum local.
$ E \ subset \ mathbb (R) ^ (n) $. $ F $ est dit avoir maximum local au point $ x_ (0) \ dans E $, s'il existe un voisinage $ U $ du point $ x_ (0) $ tel que pour tout $ x \ dans U $ l'inégalité $ f \ left (x \ right ) \ leqslant f \ left (x_ (0) \ right) $.
Le maximum local est appelé strict si le voisinage $ U $ peut être choisi de telle sorte que pour tout $ x \ dans U $ autre que $ x_ (0) $, il y ait $ f \ left (x \ right)< f\left(x_{0}\right)$.
Définition
Soit $ f $ une fonction réelle sur l'ouvert $ E \ subset \ mathbb (R) ^ (n) $. $ F $ est dit avoir minimum local au point $ x_ (0) \ dans E $, s'il existe un voisinage $ U $ du point $ x_ (0) $ tel que pour tout $ x \ dans U $ l'inégalité $ f \ left (x \ right ) \ geqslant f \ left (x_ (0) \ right) $.
Un minimum local est dit strict si le voisinage $ U $ peut être choisi de telle sorte que pour tout $ x \ in U $ autre que $ x_ (0) $, $ f \ left (x \ right)> f \ left (x_ ( 0) \ à droite) $.
L'extremum local combine les concepts de minimum local et de maximum local.
Théorème ( condition nécessaire extremum de fonction différentiable)
Soit $ f $ une fonction réelle sur l'ouvert $ E \ subset \ mathbb (R) ^ (n) $. Si au point $ x_ (0) \ dans E $ la fonction $ f $ a un extremum local en ce point, alors $$ \ text (d) f \ left (x_ (0) \ right) = 0. $$ L'égalité à zéro différentiel équivaut au fait que tous sont égaux à zéro, c'est-à-dire $$ \ displaystyle \ frac (\ partial f) (\ partial x_ (i)) \ left (x_ (0) \ right) = 0. $$
Dans le cas unidimensionnel, c'est le cas. On note $ \ phi \ left (t \ right) = f \ left (x_ (0) + th \ right) $, où $ h $ est un vecteur arbitraire. La fonction $\phi $ est définie pour des valeurs suffisamment petites de $ t $ en valeur absolue. De plus, par, il est dérivable, et $ (\ phi) '\ left (t \ right) = \ text (d) f \ left (x_ (0) + th \ right) h $.
Soit $ f $ avoir un maximum local au point x $ 0 $. Par conséquent, la fonction $ \ phi $ pour $ t = 0 $ a un maximum local et, par le théorème de Fermat, $ (\ phi) '\ left (0 \ right) = 0 $.
Donc, nous avons que $ df \ left (x_ (0) \ right) = 0 $, c'est-à-dire de la fonction $ f $ au point $ x_ (0) $ est égal à zéro sur tout vecteur $ h $.
Définition
Points auxquels le différentiel est nul, c'est-à-dire celles dans lesquelles toutes les dérivées partielles sont égales à zéro sont appelées stationnaires. Points critiques la fonction $ f $ est appelée de tels points auxquels $ f $ n'est pas dérivable, ou est égal à zéro. Si le point est stationnaire, cela ne signifie pas encore que la fonction a un extremum en ce point.
Exemple 1.
Soit $ f \ left (x, y \ right) = x ^ (3) + y ^ (3) $. Alors $ \ displaystyle \ frac (\ partial f) (\ partial x) = 3 \ cdot x ^ (2) $, $ \ displaystyle \ frac (\ partial f) (\ partial y) = 3 \ cdot y ^ (2 ) $, donc $ \ left (0,0 \ right) $ est un point stationnaire, mais à ce point la fonction n'a pas d'extremum. En effet, $ f \ left (0,0 \ right) = 0 $, mais il est facile de voir qu'à n'importe quel voisinage du point $ \ left (0,0 \ right) $ la fonction prend à la fois des valeurs positives et négatives.
Exemple 2.
La fonction $ f \ left (x, y \ right) = x ^ (2) - y ^ (2) $ a pour origine un point stationnaire, mais il est clair qu'il n'y a pas d'extremum en ce point.
Théorème (condition suffisante pour un extremum).
Soit la fonction $ f $ dérivable deux fois continûment sur l'ouvert $ E \ subset \ mathbb (R) ^ (n) $. Soit $ x_ (0) \ in E $ un point stationnaire et $$ \ displaystyle Q_ (x_ (0)) \ left (h \ right) \ equiv \ sum_ (i = 1) ^ n \ sum_ (j = 1 ) ^ n \ frac (\ partiel ^ (2) f) (\ partiel x_ (i) \ partiel x_ (j)) \ gauche (x_ (0) \ droite) h ^ (i) h ^ (j). $ $ puis
- si $ Q_ (x_ (0)) $ -, alors la fonction $ f $ au point $ x_ (0) $ a un extremum local, à savoir, un minimum si la forme est définie positive, et un maximum si la forme est défini négatif;
- si la forme quadratique $ Q_ (x_ (0)) $ n'est pas définie, alors la fonction $ f $ au point $ x_ (0) $ n'a pas d'extremum.
Utilisons le développement selon la formule de Taylor (12.7 p. 292). En tenant compte du fait que les dérivées partielles du premier ordre au point $ x_ (0) $ sont égales à zéro, on obtient $$ \ displaystyle f \ left (x_ (0) + h \ right) −f \ left (x_ (0) \ right) = \ frac (1) (2) \ sum_ (i = 1) ^ n \ sum_ (j = 1) ^ n \ frac (\ partial ^ (2) f) (\ partial x_ (i ) \ partiel x_ (j)) \ gauche (x_ (0) + \ thêta h \ droite) h ^ (i) h ^ (j), $$ où $ 0<\theta<1$. Обозначим $\displaystyle a_{ij}=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right)$. В силу теоремы Шварца (12.6 стр. 289-290) , $a_{ij}=a_{ji}$. Обозначим $$\displaystyle \alpha_{ij} \left(h\right)=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}+\theta h\right)−\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right).$$ По предположению, все непрерывны и поэтому $$\lim_{h \rightarrow 0} \alpha_{ij} \left(h\right)=0. \left(1\right)$$ Получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left.$$ Обозначим $$\displaystyle \epsilon \left(h\right)=\frac{1}{|h|^{2}}\sum_{i=1}^n \sum_{j=1}^n \alpha_{ij} \left(h\right)h_{i}h_{j}.$$ Тогда $$|\epsilon \left(h\right)| \leq \sum_{i=1}^n \sum_{j=1}^n |\alpha_{ij} \left(h\right)|$$ и, в силу соотношения $\left(1\right)$, имеем $\epsilon \left(h\right) \rightarrow 0$ при $h \rightarrow 0$. Окончательно получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left. \left(2\right)$$ Предположим, что $Q_{x_{0}}$ – положительноопределенная форма. Согласно лемме о положительноопределённой квадратичной форме (12.8.1 стр. 295, Лемма 1) , существует такое положительное число $\lambda$, что $Q_{x_{0}} \left(h\right) \geqslant \lambda|h|^{2}$ при любом $h$. Поэтому $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right) \geq \frac{1}{2}|h|^{2} \left(λ+\epsilon \left(h\right)\right).$$ Так как $\lambda>0 $, et $\epsilon\left(h\right)\rightarrow 0 $ pour $h\rightarrow 0$, alors le membre de droite sera positif pour tout vecteur $h$ de longueur suffisamment petite.
Ainsi, nous sommes arrivés à la conclusion que dans un voisinage du point $ x_ (0) $ l'inégalité $ f \ left (x \ right)> f \ left (x_ (0) \ right) $ est vraie, si seulement $ x \neq x_ (0) $ (on met $ x = x_ (0) + h $ \ right). Cela signifie qu'au point $ x_ (0) $ la fonction a un strict minimum local, et donc la première partie de notre théorème est prouvée.
Supposons maintenant que $ Q_ (x_ (0)) $ est une forme indéfinie. Alors il existe des vecteurs $ h_ (1) $, $ h_ (2) $ tels que $ Q_ (x_ (0)) \ left (h_ (1) \ right) = \ lambda_ (1)> 0 $, $ Q_ ( x_ (0)) \ gauche (h_ (2) \ droite) = \ lambda_ (2)<0$. В соотношении $\left(2\right)$ $h=th_{1}$ $t>0 $. On obtient alors $$ f \ left (x_ (0) + th_ (1) \ right) −f \ left (x_ (0) \ right) = \ frac (1) (2) \ left [t ^ (2) \ lambda_ (1) + t ^ (2) | h_ (1) | ^ (2) \ epsilon \ gauche (th_ (1) \ droite) \ droite] = \ frac (1) (2) t ^ (2) \ left [\ lambda_ (1) + | h_ (1) | ^ (2) \ epsilon \ left (th_ (1) \ right) \ right]. $$ Pour suffisamment petit $ t> 0 $ le côté droit est positif. Cela signifie que dans n'importe quel voisinage du point $ x_ (0) $ la fonction $ f $ prend des valeurs $ f \ left (x \ right) $ qui sont supérieures à $ f \ left (x_ (0) \ right) $.
De même, on obtient qu'en tout voisinage du point $ x_ (0) $ la fonction $ f $ prend des valeurs inférieures à $ f \ left (x_ (0) \ right) $. Ceci, avec le précédent, signifie qu'au point $ x_ (0) $ la fonction $ f $ n'a pas d'extremum.
Envisager cas particulier de ce théorème pour la fonction $ f \ left (x, y \ right) $ de deux variables, définies dans un voisinage du point $ \ left (x_ (0), y_ (0) \ right) $ et ayant des partiels continus dérivées du premier et du deuxième ordre. Supposons que $ \ left (x_ (0), y_ (0) \ right) $ est un point stationnaire, et notons $$ \ displaystyle a_ (11) = \ frac (\ partial ^ (2) f) (\ partial x ^ (2)) \ gauche (x_ (0), y_ (0) \ droite), a_ (12) = \ frac (\ partiel ^ (2) f) (\ partiel x \ partiel y) \ gauche (x_ ( 0 ), y_ (0) \ droite), a_ (22) = \ frac (\ partiel ^ (2) f) (\ partiel y ^ (2)) \ gauche (x_ (0), y_ (0) \ droite ) $$ Alors le théorème précédent prend la forme suivante.
Théorème
Soit $ \ Delta = a_ (11) \ cdot a_ (22) - a_ (12) ^ 2 $. Puis:
- si $ \ Delta> 0 $, alors la fonction $ f $ a un extremum local au point $ \ left (x_ (0), y_ (0) \ right) $, à savoir, un minimum si $ a_ (11)> 0 $ , et maximum si $ a_ (11)<0$;
- si $ \ Delta<0$, то экстремума в точке $\left(x_{0},y_{0}\right)$ нет. Как и в одномерном случае, при $\Delta=0$ экстремум может быть, а может и не быть.
Exemples de résolution de problèmes
Algorithme pour trouver l'extremum d'une fonction de plusieurs variables :
- Trouver des points fixes ;
- Trouver le différentiel du 2ème ordre à tous les points stationnaires
- En utilisant la condition suffisante pour l'extremum d'une fonction de plusieurs variables, on considère la différentielle du second ordre en chaque point stationnaire
- Examinez la fonction pour l'extremum $ f \ left (x, y \ right) = x ^ (3) + 8 \ cdot y ^ (3) + 18 \ cdot x - 30 \ cdot y $.
SolutionTrouvez les dérivées partielles du 1er ordre : $$ \ displaystyle \ frac (\ partial f) (\ partial x) = 3 \ cdot x ^ (2) - 6 \ cdot y; $$ $$ \ displaystyle \ frac (\ partial f ) (\ partial y) = 24 \ cdot y ^ (2) - 6 \ cdot x. $$ Composons et résolvons le système : $$ \ displaystyle \ begin (cases) \ frac (\ partial f) (\ partial x ) = 0 \\\ frac (\ partial f) (\ partial y) = 0 \ end (cases) \ Rightarrow \ begin (cases) 3 \ cdot x ^ (2) - 6 \ cdot y = 0 \\ 24 \ cdot y ^ (2) - 6 \ cdot x = 0 \ end (cases) \ Rightarrow \ begin (cases) x ^ (2) - 2 \ cdot y = 0 \\ 4 \ cdot y ^ (2) - x = 0 \ end (cases) $$ A partir de la 2ème équation, exprimez $ x = 4 \ cdot y ^ (2) $ - remplacez dans la 1ère équation : $$ \ displaystyle \ left (4 \ cdot y ^ (2) \ right ) ^ (2) -2 \ cdot y = 0 $$ $$ 16 \ cdot y ^ (4) - 2 \ cdot y = 0 $$ $$ 8 \ cdot y ^ (4) - y = 0 $$ $ $ y \ left (8 \ cdot y ^ (3) -1 \ right) = 0 $$ En conséquence, on obtient 2 points stationnaires :
1) $ y = 0 \ Rightarrow x = 0, M_ (1) = \ left (0, 0 \ right) $;
2) $ \ displaystyle 8 \ cdot y ^ (3) -1 = 0 \ Rightarrow y ^ (3) = \ frac (1) (8) \ Rightarrow y = \ frac (1) (2) \ Rightarrow x = 1 , M_ (2) = \ gauche (\ frac (1) (2), 1 \ droite) $
Vérifions la réalisation de la condition suffisante pour un extremum :
$$ \ displaystyle \ frac (\ partial ^ (2) f) (\ partial x ^ (2)) = 6 \ cdot x; \ frac (\ partiel ^ (2) f) (\ partiel x \ partiel y) = - 6; \ frac (\ partiel ^ (2) f) (\ partiel y ^ (2)) = 48 \ cdot y $$
1) Pour le point $ M_ (1) = \ gauche (0,0 \ droite) $ :
$$ \ displaystyle A_ (1) = \ frac (\ partial ^ (2) f) (\ partial x ^ (2)) \ left (0,0 \ right) = 0; B_ (1) = \ frac (\ partiel ^ (2) f) (\ partiel x \ partiel y) \ gauche (0,0 \ droite) = - 6; C_ (1) = \ frac (\ partiel ^ (2) f) (\ partiel y ^ (2)) \ gauche (0,0 \ droite) = 0; $$
$ A_ (1) \ cdot B_ (1) - C_ (1) ^ (2) = -36<0$ , значит, в точке $M_{1}$ нет экстремума.
2) Pour le point $ M_ (2) $ :
$$ \ displaystyle A_ (2) = \ frac (\ partial ^ (2) f) (\ partial x ^ (2)) \ left (1, \ frac (1) (2) \ right) = 6; B_ (2) = \ frac (\ partiel ^ (2) f) (\ partiel x \ partiel y) \ gauche (1, \ frac (1) (2) \ droite) = - 6; C_ (2) = \ frac (\ partiel ^ (2) f) (\ partiel y ^ (2)) \ gauche (1, \ frac (1) (2) \ droite) = 24; $$
$ A_ (2) \ cdot B_ (2) - C_ (2) ^ (2) = 108> 0 $, donc il y a un extremum au point $ M_ (2) $, et puisque $ A_ (2)> 0 $, alors c'est le minimum.
Réponse : Le point $ \ displaystyle M_ (2) \ left (1, \ frac (1) (2) \ right) $ est le point minimum de la fonction $ f $. - Examinez la fonction pour l'extremum $ f = y ^ (2) + 2 \ cdot x \ cdot y - 4 \ cdot x - 2 \ cdot y - 3 $.
SolutionTrouver des points stationnaires : $$ \ displaystyle \ frac (\ partial f) (\ partial x) = 2 \ cdot y - 4; $$ $$ \ displaystyle \ frac (\ partial f) (\ partial y) = 2 \ cdot y + 2 \ cdot x - 2. $$
Composons et résolvons le système : $$ \ displaystyle \ begin (cases) \ frac (\ partial f) (\ partial x) = 0 \\\ frac (\ partial f) (\ partial y) = 0 \ end (cases ) \ Rightarrow \ begin (cases) 2 \ cdot y - 4 = 0 \\ 2 \ cdot y + 2 \ cdot x - 2 = 0 \ end (cases) \ Rightarrow \ begin (cases) y = 2 \\ y + x = 1 \ end (cases) \ Rightarrow x = -1 $$
$ M_ (0) \ left (-1, 2 \ right) $ est un point stationnaire.
Vérifions que la condition extremum suffisante est satisfaite : $$ \ displaystyle A = \ frac (\ partial ^ (2) f) (\ partial x ^ (2)) \ left (-1,2 \ right) = 0; B = \ frac (\ partiel ^ (2) f) (\ partiel x \ partiel y) \ gauche (-1,2 \ droite) = 2; C = \ frac (\ partiel ^ (2) f) (\ partiel y ^ (2)) \ gauche (-1,2 \ droite) = 2; $$
$ A \ cdot B - C ^ (2) = -4<0$ , значит, в точке $M_{0}$ нет экстремума.
Réponse : il n'y a pas d'extrêmes.
Limite de temps : 0
Navigation (numéros de tâche uniquement)
0 des 4 questions terminées
Information
Répondez à ce quiz pour tester vos connaissances sur le sujet que vous venez de lire, « Extrema local des fonctions de nombreuses variables ».
Vous avez déjà fait le test auparavant. Vous ne pouvez pas le redémarrer.
Le test est en cours de chargement...
Vous devez vous connecter ou vous inscrire pour commencer le test.
Vous devez effectuer les tests suivants pour démarrer celui-ci :
résultats
Bonnes réponses : 0 sur 4
Ton temps:
Temps est révolu
Vous avez marqué 0 points sur 0 (0)
Votre résultat a été enregistré dans le classement
- Avec la réponse
- Marqué comme vu
Question 2 sur 4
2 .
Points : 1Est-ce que la fonction $ f = 4 + \ sqrt ((x ^ (2) + y ^ (2)) ^ (2)) $
Tâche 1 sur 4
1 .
Points : 1Examinez la fonction $ f $ pour les extrema : $ f = e ^ (x + y) (x ^ (2) -2 \ cdot y ^ (2)) $
À droite
Pas correctement
Le point extremum d'une fonction est un point dans le domaine d'une fonction auquel la valeur d'une fonction prend une valeur minimale ou maximale. Les valeurs de la fonction à ces points sont appelées les extrema (minimum et maximum) de la fonction.
Définition... Point X1 domaine de fonction F(X) est appelé point maximum de la fonction , si la valeur de la fonction en ce point est supérieure aux valeurs de la fonction en des points suffisamment proches d'elle, situés à droite et à gauche de celle-ci (c'est-à-dire l'inégalité F(X0 ) > F(X 0 + Δ X) X1 maximum.
Définition... Point X2 domaine de fonction F(X) est appelé le point minimum de la fonction, si la valeur de la fonction en ce point est inférieure aux valeurs de la fonction en des points suffisamment proches d'elle, situés à droite et à gauche de celle-ci (c'est-à-dire l'inégalité F(X0 ) < F(X 0 + Δ X) ). Dans ce cas, on dit que la fonction a au point X2 le minimum.
disons point X1 est le point maximum de la fonction F(X). Puis dans l'intervalle jusqu'à X1 la fonction augmente, donc la dérivée de la fonction est supérieure à zéro ( F "(X)> 0), et dans l'intervalle après X1 la fonction diminue donc et dérivée d'une fonction moins que zéro ( F "(X) < 0 ). Тогда в точке X1
Supposons également que le point X2 est le point minimum de la fonction F(X). Puis dans l'intervalle jusqu'à X2 la fonction diminue et la dérivée de la fonction est inférieure à zéro ( F "(X) < 0 ), а в интервале после X2 la fonction augmente et la dérivée de la fonction est supérieure à zéro ( F "(X)> 0). Dans ce cas, également au point X2 la dérivée de la fonction est nulle ou n'existe pas.
Théorème de Fermat (un critère nécessaire à l'existence d'un extremum d'une fonction)... Si point X0 est le point extremum de la fonction F(X), alors à ce stade la dérivée de la fonction est égale à zéro ( F "(X) = 0) ou n'existe pas.
Définition... Les points auxquels la dérivée d'une fonction est nulle ou n'existe pas sont appelés points critiques .

Exemple 1. Considérons une fonction.
À ce point X= 0, la dérivée de la fonction est égale à zéro, donc le point X= 0 est le point critique. Cependant, comme on peut le voir sur le graphe de la fonction, elle augmente sur tout le domaine de définition, donc le point X= 0 n'est pas le point extremum de cette fonction.
Ainsi, les conditions selon lesquelles la dérivée d'une fonction en un point est égale à zéro ou n'existe pas sont des conditions nécessaires pour un extremum, mais pas suffisantes, car d'autres exemples de fonctions pour lesquelles ces conditions sont satisfaites, mais la fonction n'a pas un extremum au point correspondant, peut être donné. Alors vous devez avoir suffisamment de signes, permettant de juger s'il y a un extremum à un point critique particulier et lequel est un maximum ou un minimum.
Théorème (le premier critère suffisant pour l'existence d'un extremum d'une fonction). Point critique X0 F(X), si la dérivée de la fonction change de signe en passant par ce point, et si le signe passe de "plus" à "moins", alors le point maximum, et si de "moins" à "plus", alors le point minimum .
Si près du point X0 , à gauche et à droite de celui-ci, la dérivée conserve le signe, alors cela signifie que la fonction ne décroît ou n'augmente que dans un certain voisinage du point X0 ... Dans ce cas, au point X0 il n'y a pas d'extrême.
Alors, pour déterminer les points extremum de la fonction, vous devez faire ce qui suit :
- Trouvez la dérivée de la fonction.
- Mettre la dérivée à zéro et déterminer les points critiques.
- Mentalement ou sur papier, marquer les points critiques sur l'axe numérique et déterminer les signes de la dérivée de la fonction dans les intervalles obtenus. Si le signe de la dérivée passe de "plus" à "moins", alors le point critique est le point maximum, et si de "moins" à "plus", alors le point minimum.
- Calculer la valeur de la fonction aux points extremum.

Exemple 2. Trouver les extrema d'une fonction ![]() .
.
Solution. Trouvons la dérivée de la fonction :
Mettons la dérivée à zéro pour trouver les points critiques :
![]() .
.
Étant donné que pour toutes les valeurs du "x", le dénominateur n'est pas nul, alors nous assimilons le numérateur à zéro :
Vous avez un point de basculement X= 3. Déterminons le signe de la dérivée dans les intervalles délimités par ce point :
dans la plage de moins l'infini à 3 - le signe moins, c'est-à-dire que la fonction diminue,
dans la plage de 3 à plus l'infini - le signe plus, c'est-à-dire que la fonction augmente.
c'est-à-dire point X= 3 est le point minimum.
Trouvons la valeur de la fonction au point minimum :
Ainsi, on trouve le point extremum de la fonction : (3 ; 0), et c'est le point minimum.
Théorème (le deuxième critère suffisant pour l'existence d'un extremum d'une fonction). Point critique X0 est le point extremum de la fonction F(X) si la dérivée seconde de la fonction en ce point n'est pas nulle ( F ""(X) ≠ 0), et si la dérivée seconde est supérieure à zéro ( F ""(X)> 0), alors le point maximum, et si la dérivée seconde est inférieure à zéro ( F ""(X) < 0 ), то точкой минимума.
Remarque 1. Si au point X0 les dérivées première et seconde disparaissent, alors à ce stade il est impossible de juger de la présence d'un extremum sur la base du second critère suffisant. Dans ce cas, il faut utiliser le premier indicateur suffisant de l'extremum de la fonction.
Remarque 2. Le second critère suffisant pour l'extremum d'une fonction est également inapplicable si la dérivée première n'existe pas au point stationnaire (alors la dérivée seconde n'existe pas non plus). Dans ce cas, il faut aussi utiliser le premier indicateur suffisant de l'extremum de la fonction.
Le caractère local des extrema de la fonction
Des définitions ci-dessus, il s'ensuit que l'extremum de la fonction a un caractère local - c'est le plus grand et plus petite valeur fonction par rapport aux valeurs voisines.
Supposons que vous examiniez vos revenus sur une période d'un an. Si vous avez gagné 45 000 roubles en mai, 42 000 roubles en avril et 39 000 roubles en juin, les gains de mai sont le maximum de la fonction de gains par rapport aux valeurs les plus proches. Mais en octobre, vous avez gagné 71 000 roubles, en septembre 75 000 roubles et en novembre 74 000 roubles, les gains d'octobre sont donc le minimum de la fonction de gains par rapport aux valeurs voisines. Et vous pouvez facilement voir que le maximum parmi les valeurs d'avril-mai-juin est inférieur au minimum de septembre-octobre-novembre.
D'une manière générale, sur l'intervalle, une fonction peut avoir plusieurs extrema, et il peut s'avérer que tout minimum de la fonction est supérieur à tout maximum. Ainsi, pour la fonction illustrée dans la figure ci-dessus,.
C'est-à-dire qu'il ne faut pas penser que le maximum et le minimum d'une fonction sont respectivement ses valeurs les plus grandes et les plus petites sur tout l'intervalle considéré. Au point maximum, la fonction n'a la plus grande valeur que par rapport aux valeurs qu'elle a en tous points suffisamment proches du point maximum, et au point minimum - la plus petite valeur uniquement par rapport aux valeurs qui il est en tout point assez proche du point minimum.
Par conséquent, il est possible de clarifier le concept ci-dessus de points extremum d'une fonction et d'appeler les points minimaux points minimaux locaux et points maximaux - points maximaux locaux.
À la recherche d'extrema d'une fonction ensemble

Exemple 3.
Solution : La fonction est définie et continue sur toute la droite numérique. Son dérivé ![]() existe aussi sur toute la droite numérique. Par conséquent, dans ce cas, les points critiques sont uniquement ceux auxquels, c'est-à-dire , d'où et. Points critiques et diviser l'ensemble du domaine de la fonction en trois intervalles de monotonie :. Choisissons un point de contrôle dans chacun d'eux et trouvons le signe de la dérivée en ce point.
existe aussi sur toute la droite numérique. Par conséquent, dans ce cas, les points critiques sont uniquement ceux auxquels, c'est-à-dire , d'où et. Points critiques et diviser l'ensemble du domaine de la fonction en trois intervalles de monotonie :. Choisissons un point de contrôle dans chacun d'eux et trouvons le signe de la dérivée en ce point.
Pour l'intervalle, le point de contrôle peut être : find. En prenant un point dans l'intervalle, nous obtenons, et en prenant un point dans l'intervalle, nous avons. Donc, dans les intervalles et, et dans l'intervalle. Selon le premier critère suffisant pour un extremum, il n'y a pas d'extremum au point (puisque la dérivée conserve son signe dans l'intervalle), et au point la fonction a un minimum (puisque la dérivée change de signe de moins à plus en passant à travers ce point). Retrouvons les valeurs correspondantes de la fonction :, a. Dans l'intervalle, la fonction diminue, comme dans cet intervalle, et dans l'intervalle, elle augmente, comme dans cet intervalle.
Pour clarifier la construction du graphe, nous allons trouver les points de son intersection avec les axes de coordonnées. Car, on obtient une équation dont on trouve les racines et, c'est-à-dire deux points (0; 0) et (4; 0) du graphe de la fonction. En utilisant toutes les informations obtenues, nous construisons un graphe (voir au début de l'exemple).

Exemple 4. Trouvez les extrema de la fonction et construisez son graphe.
Le domaine de la fonction est la droite numérique entière, à l'exception du point, c'est-à-dire ...
Pour raccourcir la recherche, vous pouvez utiliser le fait que cette fonction est paire, puisque  ... Son graphe est donc symétrique par rapport à l'axe Oy et l'exploration ne peut être effectuée que pour un intervalle.
... Son graphe est donc symétrique par rapport à l'axe Oy et l'exploration ne peut être effectuée que pour un intervalle.
Trouver la dérivée ![]() et les points critiques de la fonction :
et les points critiques de la fonction :
1) 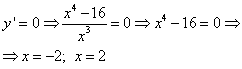 ;
;
2) ![]() ,
,
mais la fonction s'interrompt à ce stade, il ne peut donc pas s'agir d'un point extremum.
Ainsi, la fonction donnée a deux points critiques : et. Compte tenu de la parité de la fonction, vérifions uniquement le point par le deuxième critère suffisant de l'extremum. Pour ce faire, on trouve la dérivée seconde ![]() et définissez son signe à : nous obtenons. Puisque et, alors est le point minimum de la fonction, tandis que
et définissez son signe à : nous obtenons. Puisque et, alors est le point minimum de la fonction, tandis que ![]() .
.
Pour avoir une image plus complète du graphe d'une fonction, découvrons son comportement aux frontières du domaine de définition :

(ici le symbole désigne le désir Xà zéro à droite, et X reste positif; signifie également aspiration Xà zéro à gauche, et X reste négatif). Ainsi, si, alors. De plus, nous trouvons
 ,
,
celles. si donc.
Le graphique de la fonction n'a pas de points d'intersection avec les axes. L'image est au début de l'exemple.
Nous continuons à rechercher ensemble les extrema de la fonction
Exemple 8. Trouvez les extrema de la fonction.

Solution. Trouvons le domaine de la fonction. Puisque l'inégalité doit être vérifiée, nous obtenons de.
Trouvons la dérivée première de la fonction :

Trouvons les points critiques de la fonction.
$ E \ subset \ mathbb (R) ^ (n) $. $ F $ est dit avoir maximum local au point $ x_ (0) \ dans E $, s'il existe un voisinage $ U $ du point $ x_ (0) $ tel que pour tout $ x \ dans U $ l'inégalité $ f \ left (x \ right ) \ leqslant f \ left (x_ (0) \ right) $.
Le maximum local est appelé strict si le voisinage $ U $ peut être choisi de telle sorte que pour tout $ x \ dans U $ autre que $ x_ (0) $, il y ait $ f \ left (x \ right)< f\left(x_{0}\right)$.
Définition
Soit $ f $ une fonction réelle sur l'ouvert $ E \ subset \ mathbb (R) ^ (n) $. $ F $ est dit avoir minimum local au point $ x_ (0) \ dans E $, s'il existe un voisinage $ U $ du point $ x_ (0) $ tel que pour tout $ x \ dans U $ l'inégalité $ f \ left (x \ right ) \ geqslant f \ left (x_ (0) \ right) $.
Un minimum local est dit strict si le voisinage $ U $ peut être choisi de telle sorte que pour tout $ x \ in U $ autre que $ x_ (0) $, $ f \ left (x \ right)> f \ left (x_ ( 0) \ à droite) $.
L'extremum local combine les concepts de minimum local et de maximum local.
Théorème (condition nécessaire pour l'extremum d'une fonction dérivable)
Soit $ f $ une fonction réelle sur l'ouvert $ E \ subset \ mathbb (R) ^ (n) $. Si au point $ x_ (0) \ dans E $ la fonction $ f $ a un extremum local en ce point, alors $$ \ text (d) f \ left (x_ (0) \ right) = 0. $$ L'égalité à zéro différentiel équivaut au fait que tous sont égaux à zéro, c'est-à-dire $$ \ displaystyle \ frac (\ partial f) (\ partial x_ (i)) \ left (x_ (0) \ right) = 0. $$
Dans le cas unidimensionnel, c'est le cas. On note $ \ phi \ left (t \ right) = f \ left (x_ (0) + th \ right) $, où $ h $ est un vecteur arbitraire. La fonction $\phi $ est définie pour des valeurs suffisamment petites de $ t $ en valeur absolue. De plus, par, il est dérivable, et $ (\ phi) '\ left (t \ right) = \ text (d) f \ left (x_ (0) + th \ right) h $.
Soit $ f $ avoir un maximum local au point x $ 0 $. Par conséquent, la fonction $ \ phi $ pour $ t = 0 $ a un maximum local et, par le théorème de Fermat, $ (\ phi) '\ left (0 \ right) = 0 $.
Donc, nous avons que $ df \ left (x_ (0) \ right) = 0 $, c'est-à-dire de la fonction $ f $ au point $ x_ (0) $ est égal à zéro sur tout vecteur $ h $.
Définition
Points auxquels le différentiel est nul, c'est-à-dire celles dans lesquelles toutes les dérivées partielles sont égales à zéro sont appelées stationnaires. Points critiques la fonction $ f $ est appelée de tels points auxquels $ f $ n'est pas dérivable, ou est égal à zéro. Si le point est stationnaire, cela ne signifie pas encore que la fonction a un extremum en ce point.
Exemple 1.
Soit $ f \ left (x, y \ right) = x ^ (3) + y ^ (3) $. Alors $ \ displaystyle \ frac (\ partial f) (\ partial x) = 3 \ cdot x ^ (2) $, $ \ displaystyle \ frac (\ partial f) (\ partial y) = 3 \ cdot y ^ (2 ) $, donc $ \ left (0,0 \ right) $ est un point stationnaire, mais à ce point la fonction n'a pas d'extremum. En effet, $ f \ left (0,0 \ right) = 0 $, mais il est facile de voir qu'à n'importe quel voisinage du point $ \ left (0,0 \ right) $ la fonction prend à la fois des valeurs positives et négatives.
Exemple 2.
La fonction $ f \ left (x, y \ right) = x ^ (2) - y ^ (2) $ a pour origine un point stationnaire, mais il est clair qu'il n'y a pas d'extremum en ce point.
Théorème (condition suffisante pour un extremum).
Soit la fonction $ f $ dérivable deux fois continûment sur l'ouvert $ E \ subset \ mathbb (R) ^ (n) $. Soit $ x_ (0) \ in E $ un point stationnaire et $$ \ displaystyle Q_ (x_ (0)) \ left (h \ right) \ equiv \ sum_ (i = 1) ^ n \ sum_ (j = 1 ) ^ n \ frac (\ partiel ^ (2) f) (\ partiel x_ (i) \ partiel x_ (j)) \ gauche (x_ (0) \ droite) h ^ (i) h ^ (j). $ $ puis
- si $ Q_ (x_ (0)) $ -, alors la fonction $ f $ au point $ x_ (0) $ a un extremum local, à savoir, un minimum si la forme est définie positive, et un maximum si la forme est défini négatif;
- si la forme quadratique $ Q_ (x_ (0)) $ n'est pas définie, alors la fonction $ f $ au point $ x_ (0) $ n'a pas d'extremum.
Utilisons le développement selon la formule de Taylor (12.7 p. 292). En tenant compte du fait que les dérivées partielles du premier ordre au point $ x_ (0) $ sont égales à zéro, on obtient $$ \ displaystyle f \ left (x_ (0) + h \ right) −f \ left (x_ (0) \ right) = \ frac (1) (2) \ sum_ (i = 1) ^ n \ sum_ (j = 1) ^ n \ frac (\ partial ^ (2) f) (\ partial x_ (i ) \ partiel x_ (j)) \ gauche (x_ (0) + \ thêta h \ droite) h ^ (i) h ^ (j), $$ où $ 0<\theta<1$. Обозначим $\displaystyle a_{ij}=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right)$. В силу теоремы Шварца (12.6 стр. 289-290) , $a_{ij}=a_{ji}$. Обозначим $$\displaystyle \alpha_{ij} \left(h\right)=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}+\theta h\right)−\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right).$$ По предположению, все непрерывны и поэтому $$\lim_{h \rightarrow 0} \alpha_{ij} \left(h\right)=0. \left(1\right)$$ Получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left.$$ Обозначим $$\displaystyle \epsilon \left(h\right)=\frac{1}{|h|^{2}}\sum_{i=1}^n \sum_{j=1}^n \alpha_{ij} \left(h\right)h_{i}h_{j}.$$ Тогда $$|\epsilon \left(h\right)| \leq \sum_{i=1}^n \sum_{j=1}^n |\alpha_{ij} \left(h\right)|$$ и, в силу соотношения $\left(1\right)$, имеем $\epsilon \left(h\right) \rightarrow 0$ при $h \rightarrow 0$. Окончательно получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left. \left(2\right)$$ Предположим, что $Q_{x_{0}}$ – положительноопределенная форма. Согласно лемме о положительноопределённой квадратичной форме (12.8.1 стр. 295, Лемма 1) , существует такое положительное число $\lambda$, что $Q_{x_{0}} \left(h\right) \geqslant \lambda|h|^{2}$ при любом $h$. Поэтому $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right) \geq \frac{1}{2}|h|^{2} \left(λ+\epsilon \left(h\right)\right).$$ Так как $\lambda>0 $, et $\epsilon\left(h\right)\rightarrow 0 $ pour $h\rightarrow 0$, alors le membre de droite sera positif pour tout vecteur $h$ de longueur suffisamment petite.
Ainsi, nous sommes arrivés à la conclusion que dans un voisinage du point $ x_ (0) $ l'inégalité $ f \ left (x \ right)> f \ left (x_ (0) \ right) $ est vraie, si seulement $ x \neq x_ (0) $ (on met $ x = x_ (0) + h $ \ right). Cela signifie qu'au point $ x_ (0) $ la fonction a un strict minimum local, et donc la première partie de notre théorème est prouvée.
Supposons maintenant que $ Q_ (x_ (0)) $ est une forme indéfinie. Alors il existe des vecteurs $ h_ (1) $, $ h_ (2) $ tels que $ Q_ (x_ (0)) \ left (h_ (1) \ right) = \ lambda_ (1)> 0 $, $ Q_ ( x_ (0)) \ gauche (h_ (2) \ droite) = \ lambda_ (2)<0$. В соотношении $\left(2\right)$ $h=th_{1}$ $t>0 $. On obtient alors $$ f \ left (x_ (0) + th_ (1) \ right) −f \ left (x_ (0) \ right) = \ frac (1) (2) \ left [t ^ (2) \ lambda_ (1) + t ^ (2) | h_ (1) | ^ (2) \ epsilon \ gauche (th_ (1) \ droite) \ droite] = \ frac (1) (2) t ^ (2) \ left [\ lambda_ (1) + | h_ (1) | ^ (2) \ epsilon \ left (th_ (1) \ right) \ right]. $$ Pour suffisamment petit $ t> 0 $ le côté droit est positif. Cela signifie que dans n'importe quel voisinage du point $ x_ (0) $ la fonction $ f $ prend des valeurs $ f \ left (x \ right) $ qui sont supérieures à $ f \ left (x_ (0) \ right) $.
De même, on obtient qu'en tout voisinage du point $ x_ (0) $ la fonction $ f $ prend des valeurs inférieures à $ f \ left (x_ (0) \ right) $. Ceci, avec le précédent, signifie qu'au point $ x_ (0) $ la fonction $ f $ n'a pas d'extremum.
Considérons un cas particulier de ce théorème pour la fonction $ f \ left (x, y \ right) $ de deux variables, définies dans un voisinage du point $ \ left (x_ (0), y_ (0) \ right) $ et ayant des dérivées partielles continues des premier et deuxième ordres. Supposons que $ \ left (x_ (0), y_ (0) \ right) $ est un point stationnaire, et notons $$ \ displaystyle a_ (11) = \ frac (\ partial ^ (2) f) (\ partial x ^ (2)) \ gauche (x_ (0), y_ (0) \ droite), a_ (12) = \ frac (\ partiel ^ (2) f) (\ partiel x \ partiel y) \ gauche (x_ ( 0 ), y_ (0) \ droite), a_ (22) = \ frac (\ partiel ^ (2) f) (\ partiel y ^ (2)) \ gauche (x_ (0), y_ (0) \ droite ) $$ Alors le théorème précédent prend la forme suivante.
Théorème
Soit $ \ Delta = a_ (11) \ cdot a_ (22) - a_ (12) ^ 2 $. Puis:
- si $ \ Delta> 0 $, alors la fonction $ f $ a un extremum local au point $ \ left (x_ (0), y_ (0) \ right) $, à savoir, un minimum si $ a_ (11)> 0 $ , et maximum si $ a_ (11)<0$;
- si $ \ Delta<0$, то экстремума в точке $\left(x_{0},y_{0}\right)$ нет. Как и в одномерном случае, при $\Delta=0$ экстремум может быть, а может и не быть.
Exemples de résolution de problèmes
Algorithme pour trouver l'extremum d'une fonction de plusieurs variables :
- Trouver des points fixes ;
- Trouver le différentiel du 2ème ordre à tous les points stationnaires
- En utilisant la condition suffisante pour l'extremum d'une fonction de plusieurs variables, on considère la différentielle du second ordre en chaque point stationnaire
- Examinez la fonction pour l'extremum $ f \ left (x, y \ right) = x ^ (3) + 8 \ cdot y ^ (3) + 18 \ cdot x - 30 \ cdot y $.
SolutionTrouvez les dérivées partielles du 1er ordre : $$ \ displaystyle \ frac (\ partial f) (\ partial x) = 3 \ cdot x ^ (2) - 6 \ cdot y; $$ $$ \ displaystyle \ frac (\ partial f ) (\ partial y) = 24 \ cdot y ^ (2) - 6 \ cdot x. $$ Composons et résolvons le système : $$ \ displaystyle \ begin (cases) \ frac (\ partial f) (\ partial x ) = 0 \\\ frac (\ partial f) (\ partial y) = 0 \ end (cases) \ Rightarrow \ begin (cases) 3 \ cdot x ^ (2) - 6 \ cdot y = 0 \\ 24 \ cdot y ^ (2) - 6 \ cdot x = 0 \ end (cases) \ Rightarrow \ begin (cases) x ^ (2) - 2 \ cdot y = 0 \\ 4 \ cdot y ^ (2) - x = 0 \ end (cases) $$ A partir de la 2ème équation, exprimez $ x = 4 \ cdot y ^ (2) $ - remplacez dans la 1ère équation : $$ \ displaystyle \ left (4 \ cdot y ^ (2) \ right ) ^ (2) -2 \ cdot y = 0 $$ $$ 16 \ cdot y ^ (4) - 2 \ cdot y = 0 $$ $$ 8 \ cdot y ^ (4) - y = 0 $$ $ $ y \ left (8 \ cdot y ^ (3) -1 \ right) = 0 $$ En conséquence, on obtient 2 points stationnaires :
1) $ y = 0 \ Rightarrow x = 0, M_ (1) = \ left (0, 0 \ right) $;
2) $ \ displaystyle 8 \ cdot y ^ (3) -1 = 0 \ Rightarrow y ^ (3) = \ frac (1) (8) \ Rightarrow y = \ frac (1) (2) \ Rightarrow x = 1 , M_ (2) = \ gauche (\ frac (1) (2), 1 \ droite) $
Vérifions la réalisation de la condition suffisante pour un extremum :
$$ \ displaystyle \ frac (\ partial ^ (2) f) (\ partial x ^ (2)) = 6 \ cdot x; \ frac (\ partiel ^ (2) f) (\ partiel x \ partiel y) = - 6; \ frac (\ partiel ^ (2) f) (\ partiel y ^ (2)) = 48 \ cdot y $$
1) Pour le point $ M_ (1) = \ gauche (0,0 \ droite) $ :
$$ \ displaystyle A_ (1) = \ frac (\ partial ^ (2) f) (\ partial x ^ (2)) \ left (0,0 \ right) = 0; B_ (1) = \ frac (\ partiel ^ (2) f) (\ partiel x \ partiel y) \ gauche (0,0 \ droite) = - 6; C_ (1) = \ frac (\ partiel ^ (2) f) (\ partiel y ^ (2)) \ gauche (0,0 \ droite) = 0; $$
$ A_ (1) \ cdot B_ (1) - C_ (1) ^ (2) = -36<0$ , значит, в точке $M_{1}$ нет экстремума.
2) Pour le point $ M_ (2) $ :
$$ \ displaystyle A_ (2) = \ frac (\ partial ^ (2) f) (\ partial x ^ (2)) \ left (1, \ frac (1) (2) \ right) = 6; B_ (2) = \ frac (\ partiel ^ (2) f) (\ partiel x \ partiel y) \ gauche (1, \ frac (1) (2) \ droite) = - 6; C_ (2) = \ frac (\ partiel ^ (2) f) (\ partiel y ^ (2)) \ gauche (1, \ frac (1) (2) \ droite) = 24; $$
$ A_ (2) \ cdot B_ (2) - C_ (2) ^ (2) = 108> 0 $, donc il y a un extremum au point $ M_ (2) $, et puisque $ A_ (2)> 0 $, alors c'est le minimum.
Réponse : Le point $ \ displaystyle M_ (2) \ left (1, \ frac (1) (2) \ right) $ est le point minimum de la fonction $ f $. - Examinez la fonction pour l'extremum $ f = y ^ (2) + 2 \ cdot x \ cdot y - 4 \ cdot x - 2 \ cdot y - 3 $.
SolutionTrouver des points stationnaires : $$ \ displaystyle \ frac (\ partial f) (\ partial x) = 2 \ cdot y - 4; $$ $$ \ displaystyle \ frac (\ partial f) (\ partial y) = 2 \ cdot y + 2 \ cdot x - 2. $$
Composons et résolvons le système : $$ \ displaystyle \ begin (cases) \ frac (\ partial f) (\ partial x) = 0 \\\ frac (\ partial f) (\ partial y) = 0 \ end (cases ) \ Rightarrow \ begin (cases) 2 \ cdot y - 4 = 0 \\ 2 \ cdot y + 2 \ cdot x - 2 = 0 \ end (cases) \ Rightarrow \ begin (cases) y = 2 \\ y + x = 1 \ end (cases) \ Rightarrow x = -1 $$
$ M_ (0) \ left (-1, 2 \ right) $ est un point stationnaire.
Vérifions que la condition extremum suffisante est satisfaite : $$ \ displaystyle A = \ frac (\ partial ^ (2) f) (\ partial x ^ (2)) \ left (-1,2 \ right) = 0; B = \ frac (\ partiel ^ (2) f) (\ partiel x \ partiel y) \ gauche (-1,2 \ droite) = 2; C = \ frac (\ partiel ^ (2) f) (\ partiel y ^ (2)) \ gauche (-1,2 \ droite) = 2; $$
$ A \ cdot B - C ^ (2) = -4<0$ , значит, в точке $M_{0}$ нет экстремума.
Réponse : il n'y a pas d'extrêmes.
Limite de temps : 0
Navigation (numéros de tâche uniquement)
0 des 4 questions terminées
Information
Répondez à ce quiz pour tester vos connaissances sur le sujet que vous venez de lire, « Extrema local des fonctions de nombreuses variables ».
Vous avez déjà fait le test auparavant. Vous ne pouvez pas le redémarrer.
Le test est en cours de chargement...
Vous devez vous connecter ou vous inscrire pour commencer le test.
Vous devez effectuer les tests suivants pour démarrer celui-ci :
résultats
Bonnes réponses : 0 sur 4
Ton temps:
Temps est révolu
Vous avez marqué 0 points sur 0 (0)
Votre résultat a été enregistré dans le classement
- Avec la réponse
- Marqué comme vu
Question 2 sur 4
2 .
Points : 1Est-ce que la fonction $ f = 4 + \ sqrt ((x ^ (2) + y ^ (2)) ^ (2)) $
Tâche 1 sur 4
1 .
Points : 1Examinez la fonction $ f $ pour les extrema : $ f = e ^ (x + y) (x ^ (2) -2 \ cdot y ^ (2)) $
À droite
Pas correctement
Définition: Le point x0 est appelé le point du maximum (ou minimum) local de la fonction si dans un certain voisinage du point x0 la fonction prend la valeur la plus grande (ou la plus petite), c'est-à-dire pour tout х à partir d'un voisinage du point х0, la condition f (x) f (x0) (ou f (x) f (x0)) est satisfaite.
Les points du maximum ou du minimum local sont réunis par un nom commun - les points de l'extremum local de la fonction.
Notez qu'aux points d'un extremum local, la fonction n'atteint sa valeur maximale ou minimale que dans une certaine zone locale. Il existe des cas où la valeur de maxуmin.
Un critère nécessaire à l'existence d'un extremum local d'une fonction
Théorème ... Si une fonction continue y = f (x) a un extremum local en un point x0, alors à ce point la dérivée première s'annule ou n'existe pas, c'est-à-dire un extremum local se produit aux points critiques du premier type.
Aux points de l'extremum local, soit la tangente est parallèle à l'axe 0x, soit il y a deux tangentes (voir figure). Notez que les points critiques sont une condition nécessaire mais insuffisante pour un extremum local. Un extremum local n'a lieu qu'aux points critiques du premier type, mais tous les points critiques n'ont pas d'extremum local.
Par exemple : une parabole cubique y = x3, a un point critique x0 = 0, dans lequel la dérivéeу / (0) = 0, mais le point critique х0 = 0 n'est pas un point extremum, mais il existe un point d'inflexion (voir ci-dessous).
Un critère suffisant pour l'existence d'un extremum local d'une fonction
Théorème ... Si, lorsque l'argument passe par un point critique du premier genre de gauche à droite, la dérivée première y / (x)
change de signe de « + » à « - », alors la fonction continue y (x) en ce point critique a un maximum local ;
change de signe de "-" à "+", alors la fonction continue y (x) a un minimum local en ce point critique
ne change pas de signe, alors à ce point critique il n'y a pas d'extremum local, ici il y a un point d'inflexion.
Pour un maximum local, la région de fonction croissante (y/0) est remplacée par la région de fonction décroissante (y/0). Pour un minimum local, la région de fonction décroissante (y/0) est remplacée par la région de fonction croissante (y/0).
Exemple : examinez la fonction y = x3 + 9x2 + 15x - 9 pour la monotonie, l'extremum et construisez un graphique de la fonction.
Trouvons les points critiques du premier type en déterminant la dérivée (y/) et en l'équivalant à zéro : y/ = 3x2 + 18x + 15 = 3 (x2 + 6x + 5) = 0
Résolvons le trinôme carré en utilisant le discriminant :
x2 + 6x + 5 = 0 (a = 1, b = 6, c = 5) D =, x1k = -5, x2k = -1.
2) Nous divisons l'axe numérique par des points critiques en 3 régions et déterminons les signes de la dérivée (y /) en eux. A l'aide de ces signes, nous trouverons des zones de monotonie (augmentation et diminution) des fonctions, et à partir du changement de signes, nous déterminerons les points d'extremum locaux (maximum et minimum).
Les résultats de la recherche seront présentés sous la forme d'un tableau, à partir duquel on peut tirer les conclusions suivantes :
- 1. Sur l'intervalle у / (- 10) 0, la fonction croît de façon monotone (le signe de la dérivée у a été estimé à partir du point de contrôle x = -10, pris dans cet intervalle) ;
- 2. Sur l'intervalle (-5 ; -1) y / (- 2) 0, la fonction décroît de façon monotone (le signe de la dérivée y a été estimé à partir du point de contrôle x = -2 pris dans cet intervalle) ;
- 3. Sur l'intervalle у / (0) 0, la fonction croît de façon monotone (le signe de la dérivée у a été estimé à partir du point de contrôle x = 0 pris dans cet intervalle) ;
- 4. En passant par le point critique х1к = -5, la dérivée change de signe de "+" à "-", donc ce point est un point de maximum local
- (ymax (-5) = (-5) 3 + 9 (-5) 2 +15 (-5) -9 = -125 + 225 - 75 - 9 = 16);
- 5. En passant par le point critique х2к = -1, la dérivée change de signe de "-" à "+", donc ce point est un point de minimum local
- (ymin (-1) = -1 + 9 - 15 - 9 = - 16).
x -5 (-5; -1) -1
3) Nous construirons un graphique en fonction des résultats de l'étude avec l'implication de calculs supplémentaires des valeurs de la fonction aux points de contrôle :
construire un système de coordonnées rectangulaires Oxy ;
montrer par les coordonnées des points maximum (-5; 16) et minimum (-1; -16);
pour affiner le graphique, on calcule la valeur de la fonction aux points de contrôle, en les choisissant à gauche et à droite des points maximum et minimum et dans l'intervalle moyen, par exemple : y (-6) = (- 6) 3 +9 (-6) 2 + 15 (-6 ) -9 = 9; y (-3) = (- 3) 3 + 9 (-3) 2 + 15 (-3) -9 = 0 ;
y (0) = -9 (-6; 9); (-3; 0) et (0; -9) - points de contrôle calculés qui sont tracés pour construire un graphique ;
nous montrons le graphique sous la forme d'une courbe avec un renflement vers le haut au point maximum et un renflement vers le bas au point minimum et passant par les points de contrôle calculés.