
Logarithmic function of the inequality equation. Logarithmic inequalities. Basic logarithmic identity
Logarithmic equations and inequalities V USE options dedicated to mathematics task C3 . Every student should learn how to solve tasks C3 from the Unified State Examination in mathematics if he wants to pass the upcoming exam as “good” or “excellent”. This article presents short review frequently encountered logarithmic equations and inequalities, as well as the main methods for solving them.
So let's take a look at some examples today. logarithmic equations and inequalities, which were offered to students in the USE variants in mathematics of past years. But he will begin with a brief summary of the main theoretical points that we will need to solve them.
logarithmic function
Definition
View function
0,\, a\ne 1 \]" title="Rendered by QuickLaTeX.com">!}
called logarithmic function.
Basic properties
Basic properties of the logarithmic function y= log a x:
The plot of the logarithmic function is logarithmic curve:
Properties of logarithms
Logarithm of the product two positive numbers is equal to the sum of the logarithms of these numbers:
Title="Rendered by QuickLaTeX.com">!}
Logarithm of the quotient two positive numbers is equal to the difference of the logarithms of these numbers:
Title="Rendered by QuickLaTeX.com">!}
If a And b a≠ 1, then for any number r fair equality:
Title="Rendered by QuickLaTeX.com">!}
Equality log a t= log a s, Where a > 0, a ≠ 1, t > 0, s> 0 is true if and only if t = s.
If a, b, c are positive numbers, and a And c are different from unity, then the equality ( conversion formula to the new base of the logarithm):
Title="Rendered by QuickLaTeX.com">!}
Theorem 1. If f(x) > 0 and g(x) > 0, then logarithmic equation log a f(x) = log a g(x) (Where a > 0, a≠ 1) is equivalent to the equation f(x) = g(x).
Solving logarithmic equations and inequalities
Example 1 Solve the equation:
Solution. The range of acceptable values includes only those x, for which the expression under the sign of the logarithm is greater than zero. These values are determined next system inequalities:
Title="Rendered by QuickLaTeX.com">!}

Taking into account the fact that
Title="Rendered by QuickLaTeX.com">!}
we obtain an interval that determines the area of admissible values of this logarithmic equation:
![]()
Based on Theorem 1, all the conditions of which are satisfied here, we pass to the following equivalent quadratic equation:
Only the first root is included in the range of acceptable values.
Answer: x=7.
Example 2 Solve the equation:
Solution. The range of admissible values of the equation is determined by the system of inequalities:
ql-right-eqno">
Solution. The range of admissible values of the equation is easily defined here: x > 0.
We use substitution:
The equation takes the form:

Back substitution:

Both response enter the range of admissible values of the equation, since they are positive numbers.
Example 4 Solve the equation:
Solution. Let's start the solution again by determining the range of admissible values of the equation. It is defined by the following system of inequalities:
ql-right-eqno">
The bases of the logarithms are the same, so in the range of valid values, you can go to the following quadratic equation:
The first root is not included in the range of admissible values of the equation, the second one is included.
Answer: x = -1.
Example 5 Solve the equation:
![]()
Solution. We will look for solutions in the interval x > 0, x≠1. Let's transform the equation to an equivalent one:
Both response are within the range of admissible values of the equation.
Example 6 Solve the equation:
Solution. The system of inequalities that defines the range of admissible values of the equation, this time has the form:
Title="Rendered by QuickLaTeX.com">!}
Using the properties of the logarithm, we transform the equation to an equivalent equation in the range of permissible values:
![]()
Using the formula for the transition to a new base of the logarithm, we get:
Only one is within the allowed range. answer: x = 4.
Let's move on to logarithmic inequalities . This is exactly what you will have to deal with on the exam in mathematics. To solve further examples, we need the following theorem:
Theorem 2. If f(x) > 0 and g(x) > 0, then:
at a> 1 logarithmic inequality log a f(x) > log a g(x) is equivalent to an inequality of the same meaning: f(x) > g(x);
at 0< a < 1 логарифмическое неравенство log a f(x) > log a g(x) is equivalent to an inequality of the opposite meaning: f(x) < g(x).
Example 7 Solve the inequality:
Solution. Let's start by defining the range of acceptable values of inequality. The expression under the sign of the logarithmic function must take only positive values. This means that the desired range of acceptable values is determined by the following system of inequalities:
Title="Rendered by QuickLaTeX.com">!}
Since the base of the logarithm is a number less than one, the corresponding logarithmic function will be decreasing, and therefore, according to Theorem 2, the transition to the following quadratic inequality will be equivalent:
Finally, taking into account the range of permissible values, we obtain answer:
Example 8 Solve the inequality:
Solution. Let's start again by defining the range of acceptable values:
Title="Rendered by QuickLaTeX.com">!}
On the set of admissible values of the inequality, we carry out equivalent transformations:

After reduction and transition to an inequality equivalent by Theorem 2, we obtain:
Taking into account the range of permissible values, we obtain the final answer:
Example 9 Solve the logarithmic inequality:
Solution. The range of acceptable values of inequality is determined by the following system:
Title="Rendered by QuickLaTeX.com">!}
It can be seen that in the region of admissible values, the expression at the base of the logarithm is always greater than one, and therefore, according to Theorem 2, the transition to the following inequality will be equivalent:

Taking into account the range of acceptable values, we obtain the final answer:

Example 10 Solve the inequality:

Solution.
The area of acceptable values of inequality is determined by the system of inequalities:
Title="Rendered by QuickLaTeX.com">!}
I way. Let us use the formula for the transition to a new base of the logarithm and proceed to an inequality that is equivalent in the region of admissible values.
Solving logarithmic inequalities, we use the monotonicity property of the logarithmic function. We also use the definition of the logarithm and basic logarithmic formulas.
Let's recap what logarithms are:
Logarithm a positive number in the base is an indicator of the power to which you need to raise to get .
Wherein
Basic logarithmic identity:
Basic formulas for logarithms:
(The logarithm of the product is equal to the sum of the logarithms)
(The logarithm of the quotient is equal to the difference of the logarithms)
(Formula for the logarithm of the degree)
The formula for moving to a new base is:
Algorithm for solving logarithmic inequalities
We can say that logarithmic inequalities are solved according to a certain algorithm. We need to write down the range of acceptable values (ODV) of the inequality. Bring the inequality to the form The sign here can be any: It is important that the left and right in the inequality were logarithms in the same base.
And after that we “discard” the logarithms! Moreover, if the base of the degree is , the inequality sign remains the same. If the base is such that the sign of the inequality is reversed.
Of course, we don't just "knock out" logarithms. We use the monotonicity property of the logarithmic function. If the base of the logarithm is greater than one, the logarithmic function is monotonically increasing, and then greater value x corresponds to the greater value of the expression .
If the base is greater than zero and less than one, the logarithmic function decreases monotonically. A larger value of the argument x will correspond to a smaller value
Important note: it is best to write the solution as a chain of equivalent transitions.
Let's move on to practice. As always, we start with the simplest inequalities.
1. Consider the inequality log 3 x > log 3 5.
Since logarithms are only defined for positive numbers, x must be positive. The condition x > 0 is called the range of acceptable values (ODV) of the given inequality. Only for such x does the inequality make sense.
Well, this wording sounds famously and is easy to remember. But why can we still do it?
We are human, we are intelligent. Our mind is arranged in such a way that everything logical, understandable, having internal structure is remembered and applied much better than random and unrelated facts. That is why it is important not to memorize the rules mechanically, like a trained mathematician dog, but to act consciously.
So why do we still "discard logarithms"?
The answer is simple: if the base is greater than one (as in our case), the logarithmic function is monotonically increasing, which means that a larger value of x corresponds to a larger value of y, and from the inequality log 3 x 1 > log 3 x 2 it follows that x 1 > x 2. 
Please note that we have switched to an algebraic inequality, and the inequality sign is preserved at the same time.
So x > 5.
The following logarithmic inequality is also simple.
2. log 5 (15 + 3x) > log 5 2x
Let's start with the range of acceptable values. Logarithms are only defined for positive numbers, so
Solving this system, we get: x > 0.
Now let's move on from the logarithmic inequality to the algebraic one - we "discard" the logarithms. Since the base of the logarithm is greater than one, the inequality sign is preserved.
15 + 3x > 2x.
We get: x > −15.
Answer: x > 0.
But what happens if the base of the logarithm is less than one? It is easy to guess that in this case, when passing to an algebraic inequality, the inequality sign will change.
Let's take an example.
Let's write the ODZ. The expressions from which logarithms are taken must be positive, that is,
Solving this system, we get: x > 4.5.
Since , the base logarithmic function decreases monotonically. And this means that a larger value of the function corresponds to a smaller value of the argument: 
And if , then
2x − 9 ≤ x.
We get that x ≤ 9.
Given that x > 4.5, we write the answer:
In the following problem, the exponential inequality is reduced to a quadratic one. So we recommend repeating the topic “square inequalities”.
Now more complex inequalities:
4. Solve the inequality

5. Solve the inequality
If , then . We were lucky! We know that the base of the logarithm is greater than one for all x values in the DPV.
Let's make a replacement

Note that we first completely solve the inequality with respect to the new variable t. And only after that we return to the variable x. Remember this and do not make mistakes on the exam!
Let's remember the rule: if there are roots, fractions or logarithms in the equation or inequality, the solution must start from the range of acceptable values. Since the base of the logarithm must be positive and not equal to one, we get a system of conditions:
Let's simplify this system:
This is the range of acceptable values for inequality.
We see that the variable is contained in the base of the logarithm. Let's move on to the permanent base. Recall that
In this case, it is convenient to go to base 4.
Let's make a replacement
Simplify the inequality and solve it using the interval method:

Back to the variable x:

We have added a condition x> 0 (from ODZ).
7. The following problem is also solved using the interval method
As always, we start the solution of the logarithmic inequality from the range of acceptable values. In this case
This condition must necessarily be fulfilled, and we will return to it. Let's take a look at the inequality itself. Let's write the left side as a base 3 logarithm:
The right side can also be written as a logarithm to base 3, and then go to the algebraic inequality:
We see that the condition (that is, the ODZ) is now automatically fulfilled. Well, this simplifies the solution of the inequality.
We solve the inequality by the interval method:
 Answer:
Answer:
Happened? Well, let's increase the difficulty level:
8. Solve the inequality:
The inequality is equivalent to the system:
9. Solve the inequality:
Expression 5 - x 2 is obsessively repeated in the condition of the problem. And this means that you can make a replacement:
Because the exponential function takes only positive values, t> 0. Then
The inequality will take the form:
Already better. Let us find the range of admissible values of the inequality. We have already said that t> 0. In addition, ( t− 3) (5 9 t − 1) > 0
If this condition is satisfied, then the quotient will also be positive.
And the expression under the logarithm on the right side of the inequality must be positive, that is, (625 t − 2) 2 .
This means that 625 t− 2 ≠ 0, i.e.
Carefully write down the ODZ
and solve the resulting system using the interval method.
 So,
So,
Well, half the battle is done - we figured out the ODZ. Let's solve the inequality. The sum of the logarithms on the left side is represented as the logarithm of the product.
Logarithmic inequalities
In previous lessons, we got acquainted with logarithmic equations and now we know what they are and how to solve them. And today's lesson will be devoted to the study of logarithmic inequalities. What are these inequalities and what is the difference between solving a logarithmic equation and inequalities?
Logarithmic inequalities are inequalities that have a variable under the sign of the logarithm or at its base.
Or, one can also say that a logarithmic inequality is an inequality in which its unknown value, as in the logarithmic equation, will be under the sign of the logarithm.
The simplest logarithmic inequalities look like this:
where f(x) and g(x) are some expressions that depend on x.
Let's look at this using the following example: f(x)=1+2x+x2, g(x)=3x−1.
Solving logarithmic inequalities
Before solving logarithmic inequalities, it is worth noting that when they are solved, they are similar to exponential inequalities, namely:
First, when moving from logarithms to expressions under the sign of the logarithm, we also need to compare the base of the logarithm with one;
Secondly, when solving a logarithmic inequality using a change of variables, we need to solve inequalities with respect to the change until we get the simplest inequality.
But it was we who considered the similar moments of solving logarithmic inequalities. Now let's look at a rather significant difference. You and I know that the logarithmic function has a limited domain of definition, so when moving from logarithms to expressions that are under the sign of the logarithm, you need to take into account the range of acceptable values (ODV).
That is, it should be borne in mind that when solving a logarithmic equation, we can first find the roots of the equation, and then check this solution. But solving the logarithmic inequality will not work this way, since moving from logarithms to expressions under the sign of the logarithm, it will be necessary to write down the ODZ of the inequality.
In addition, it is worth remembering that the theory of inequalities consists of real numbers, which are positive and negative numbers, as well as the number 0.
For example, when the number "a" is positive, then the following notation must be used: a > 0. In this case, both the sum and the product of such these numbers will also be positive.
The basic principle of solving an inequality is to replace it with a simpler inequality, but the main thing is that it be equivalent to the given one. Further, we also obtained an inequality and again replaced it with one that has a simpler form, and so on.
Solving inequalities with a variable, you need to find all its solutions. If two inequalities have the same variable x, then such inequalities are equivalent, provided that their solutions are the same.
When performing tasks for solving logarithmic inequalities, it is necessary to remember that when a > 1, then the logarithmic function increases, and when 0< a < 1, то такая функция имеет свойство убывать. Эти свойства вам будут необходимы при решении логарифмических неравенств, поэтому вы их должны хорошо знать и помнить.
Ways to solve logarithmic inequalities
Now let's look at some of the methods that take place when solving logarithmic inequalities. For a better understanding and assimilation, we will try to understand them using specific examples.
We know that the simplest logarithmic inequality has the following form:
In this inequality, V - is one of such inequality signs as:<,>, ≤ or ≥.
When the base of this logarithm is greater than one (a>1), making the transition from logarithms to expressions under the sign of the logarithm, then in this version the inequality sign is preserved, and the inequality will look like this:
which is equivalent to the following system:

In the case when the base of the logarithm is greater than zero and less than one (0 This is equivalent to this system: Let's look at more examples of solving the simplest logarithmic inequalities shown in the picture below: Exercise. Let's try to solve this inequality: The decision of the area of admissible values. Now let's try to multiply its right side by: Let's see what we can do: Now, let's move on to the transformation of sublogarithmic expressions. Since the base of the logarithm is 0< 1/4 <1, то от сюда следует, что знак неравенства изменится на противоположный: 3x - 8 > 16; And from this it follows that the interval that we have obtained belongs entirely to the ODZ and is a solution to such an inequality. Here is the answer we got: Now let's try to analyze what we need to successfully solve logarithmic inequalities? First, focus all your attention and try not to make mistakes when performing the transformations that are given in this inequality. Also, it should be remembered that when solving such inequalities, it is necessary to prevent expansions and narrowings of the ODZ inequality, which can lead to the loss or acquisition of extraneous solutions. Secondly, when solving logarithmic inequalities, you need to learn to think logically and understand the difference between such concepts as a system of inequalities and a set of inequalities, so that you can easily select solutions to an inequality, while being guided by its DHS. Thirdly, in order to successfully solve such inequalities, each of you must know perfectly all the properties elementary functions and clearly understand their meaning. Such functions include not only logarithmic, but also rational, power, trigonometric, etc., in a word, all those that you studied throughout schooling algebra. As you can see, having studied the topic of logarithmic inequalities, there is nothing difficult in solving these inequalities, provided that you are attentive and persistent in achieving your goals. In order to avoid any problems in solving inequalities, you need to train as much as possible, solving various tasks and at the same time memorize the main ways of solving such inequalities and their systems. With unsuccessful solutions to logarithmic inequalities, you should carefully analyze your mistakes so that you do not return to them again in the future. For better assimilation of the topic and consolidation of the material covered, solve the following inequalities: With them are inside logarithms. Examples: \(\log_3x≥\log_39\) Any logarithmic inequality should be reduced to the form \(\log_a(f(x)) ˅ \log_a(g(x))\) (symbol \(˅\) means any of ). This form allows us to get rid of logarithms and their bases by passing to the inequality of expressions under logarithms, that is, to the form \(f(x) ˅ g(x)\). But when making this transition, there is one very important subtlety: \(\log_2((8-x))<1\) Solution: \(\log\)\(_(0.5)\) \((2x-4)\)≥\(\log\)\(_(0.5)\) \(((x+ 1))\) Solution: Very important! In any inequality, the transition from the form \(\log_a(f(x)) ˅ \log_a(g(x))\) to comparing expressions under logarithms can only be done if: Example
. Solve the inequality: \(\log\)\(≤-1\) Solution:
\(\log\) \(_(\frac(1)(3))(\frac(3x-2)(2x-3))\)\(≤-1\) Let's write out the ODZ. ODZ: \(\frac(3x-2)(2x-3)\) \(>0\) \(\frac(3x-2-3(2x-3))(2x-3)\)\(≥\) \(0\) We open the brackets, give . \(\frac(-3x+7)(2x-3)\) \(≥\) \(0\) We multiply the inequality by \(-1\), remembering to reverse the comparison sign. \(\frac(3x-7)(2x-3)\) \(≤\) \(0\) \(\frac(3(x-\frac(7)(3)))(2(x-\frac(3)(2)))\)\(≤\) \(0\) Let's build a number line and mark the points \(\frac(7)(3)\) and \(\frac(3)(2)\) on it. Note that the point from the denominator is punctured, despite the fact that the inequality is not strict. The fact is that this point will not be a solution, since when substituting into an inequality, it will lead us to division by zero. Now we plot the ODZ on the same numerical axis and write down in response the interval that falls into the ODZ. Write down the final answer. Example
. Solve the inequality: \(\log^2_3x-\log_3x-2>0\) Solution:
\(\log^2_3x-\log_3x-2>0\) Let's write out the ODZ. ODZ: \(x>0\) Let's get to the decision. Solution: \(\log^2_3x-\log_3x-2>0\) Before us is a typical square-logarithmic inequality. We do. \(t=\log_3x\) \(D=1+8=9\) Now you need to return to the original variable - x. To do this, we pass to , which has the same solution, and make the reverse substitution. \(\left[ \begin(gathered) t>2 \\ t<-1 \end{gathered} \right.\) \(\Leftrightarrow\) \(\left[ \begin{gathered} \log_3x>2 \\ \log_3x<-1 \end{gathered} \right.\) Transform \(2=\log_39\), \(-1=\log_3\frac(1)(3)\). \(\left[ \begin(gathered) \log_3x>\log_39 \\ \log_3x<\log_3\frac{1}{3} \end{gathered} \right.\) Let's move on to comparing arguments. The bases of logarithms are greater than \(1\), so the sign of the inequalities does not change. \(\left[ \begin(gathered) x>9 \\ x<\frac{1}{3} \end{gathered} \right.\) Let's combine the solution of the inequality and the ODZ in one figure. Let's write down the answer. LOGARITHMIC INEQUALITIES IN THE USE
Sechin Mikhail Alexandrovich Small Academy of Sciences for Students of the Republic of Kazakhstan "Seeker" MBOU "Soviet secondary school No. 1", grade 11, town. Sovietsky Soviet District Gunko Lyudmila Dmitrievna, teacher of MBOU "Soviet secondary school No. 1" Sovietsky district Goal of the work: study of the mechanism for solving C3 logarithmic inequalities using non-standard methods, revealing interesting facts about the logarithm. Subject of study:
3) Learn to solve specific logarithmic C3 inequalities using non-standard methods. Results:
Content
Introduction…………………………………………………………………………….4
Chapter 1. Background………………………………………………………...5
Chapter 2. Collection of logarithmic inequalities ………………………… 7
2.1. Equivalent transitions and the generalized method of intervals…………… 7 2.2. Rationalization method …………………………………………………… 15 2.3. Non-standard substitution…………………………………………………………………………………………………. ..... 22 2.4. Tasks with traps……………………………………………………… 27 Conclusion…………………………………………………………………… 30
Literature……………………………………………………………………. 31
Introduction
I am in the 11th grade and I plan to enter a university where mathematics is a core subject. And that's why I work a lot with the tasks of part C. In task C3, you need to solve a non-standard inequality or a system of inequalities, usually associated with logarithms. While preparing for the exam, I encountered the problem of the lack of methods and techniques for solving the examination logarithmic inequalities offered in C3. The methods that are studied in the school curriculum on this topic do not provide a basis for solving tasks C3. The math teacher suggested that I work with the C3 assignments on my own under her guidance. In addition, I was interested in the question: are there logarithms in our life? With this in mind, the theme was chosen: "Logarithmic inequalities in the exam"
Goal of the work: study of the mechanism for solving C3 problems using non-standard methods, revealing interesting facts about the logarithm. Subject of study:
1) Find the necessary information about non-standard methods for solving logarithmic inequalities. 2) Find additional information about logarithms. 3) Learn to solve specific C3 problems using non-standard methods. Results:
The practical significance lies in the expansion of the apparatus for solving problems C3. This material can be used in some lessons, for conducting circles, optional classes in mathematics. The project product will be the collection "Logarithmic C3 inequalities with solutions". Chapter 1. Background
During the 16th century, the number of approximate calculations increased rapidly, primarily in astronomy. The improvement of instruments, the study of planetary movements, and other work required colossal, sometimes many years, calculations. Astronomy was in real danger of drowning in unfulfilled calculations. Difficulties also arose in other areas, for example, in the insurance business, tables of compound interest were needed for various percentage values. The main difficulty was multiplication, division of multi-digit numbers, especially trigonometric quantities. The discovery of logarithms was based on the well-known properties of progressions by the end of the 16th century. Archimedes spoke about the connection between the members of the geometric progression q, q2, q3, ... and the arithmetic progression of their indicators 1, 2, 3, ... in the Psalmite. Another prerequisite was the extension of the concept of degree to negative and fractional exponents. Many authors have pointed out that multiplication, division, raising to a power, and extracting a root exponentially correspond in arithmetic - in the same order - addition, subtraction, multiplication and division. Here was the idea of the logarithm as an exponent. In the history of the development of the doctrine of logarithms, several stages have passed. Stage 1
Logarithms were invented no later than 1594 independently by the Scottish baron Napier (1550-1617) and ten years later by the Swiss mechanic Burgi (1552-1632). Both wanted to provide a new convenient means of arithmetic calculations, although they approached this problem in different ways. Napier kinematically expressed the logarithmic function and thus entered a new field of function theory. Bürgi remained on the basis of consideration of discrete progressions. However, the definition of the logarithm for both is not similar to the modern one. The term "logarithm" (logarithmus) belongs to Napier. It arose from a combination of Greek words: logos - "relationship" and ariqmo - "number", which meant "number of relations". Initially, Napier used a different term: numeri artificiales - "artificial numbers", as opposed to numeri naturalts - "natural numbers". In 1615, in a conversation with Henry Briggs (1561-1631), a professor of mathematics at Gresh College in London, Napier suggested taking zero for the logarithm of one, and 100 for the logarithm of ten, or, what amounts to the same, just 1. This is how decimal logarithms and The first logarithmic tables were printed. Later, the Briggs tables were supplemented by the Dutch bookseller and mathematician Andrian Flakk (1600-1667). Napier and Briggs, although they came to logarithms before anyone else, published their tables later than others - in 1620. The signs log and Log were introduced in 1624 by I. Kepler. The term "natural logarithm" was introduced by Mengoli in 1659, followed by N. Mercator in 1668, and the London teacher John Spadel published tables of natural logarithms of numbers from 1 to 1000 under the name "New Logarithms". In Russian, the first logarithmic tables were published in 1703. But in all logarithmic tables, errors were made in the calculation. The first error-free tables were published in 1857 in Berlin in the processing of the German mathematician K. Bremiker (1804-1877). Stage 2
Further development of the theory of logarithms is associated with a wider application of analytic geometry and infinitesimal calculus. By that time, the connection between the quadrature of an equilateral hyperbola and the natural logarithm was established. The theory of logarithms of this period is associated with the names of a number of mathematicians. German mathematician, astronomer and engineer Nikolaus Mercator in his essay "Logarithmotechnics" (1668) gives a series that gives the expansion of ln(x + 1) in terms of powers x: This expression corresponds exactly to the course of his thought, although, of course, he did not use the signs d, ..., but more cumbersome symbols. With the discovery of the logarithmic series, the technique for calculating logarithms changed: they began to be determined using infinite series. In his lectures "Elementary mathematics from a higher point of view", read in 1907-1908, F. Klein suggested using the formula as a starting point for constructing the theory of logarithms. Stage 3
Definition of a logarithmic function as a function of the inverse exponential, logarithm as an exponent of a given base was not formulated immediately. The work of Leonhard Euler (1707-1783) "Introduction to the analysis of infinitesimals" (1748) served as further development of the theory of the logarithmic function. Thus, 134 years have passed since logarithms were first introduced (counting from 1614) before mathematicians came up with a definition the concept of the logarithm, which is now the basis of the school course. Chapter 2. Collection of logarithmic inequalities
2.1. Equivalent transitions and the generalized method of intervals. Equivalent transitions
Generalized interval method
This method most universal in solving inequalities of almost any type. The solution scheme looks like this: 1. Bring the inequality to such a form, where the function is located on the left side 2. Find the scope of the function 3. Find the zeros of a function 4. Draw the domain of definition and zeros of the function on a real line. 5. Determine the signs of the function 6. Select the intervals where the function takes the necessary values, and write down the answer. Example 1
Solution:
Apply the interval method where For these values, all expressions under the signs of logarithms are positive. Answer:
Example 2
Solution:
1st
way
.
ODZ is determined by the inequality x> 3. Taking logarithms for such x in base 10, we get The last inequality could be solved by applying the decomposition rules, i.e. comparing factors with zero. However, in this case it is easy to determine the intervals of constancy of the function so the interval method can be applied. Function f(x) = 2x(x- 3.5)lgǀ x- 3ǀ is continuous for x> 3 and vanishes at points x 1 = 0, x 2 = 3,5, x 3 = 2, x 4 = 4. Thus, we determine the intervals of constancy of the function f(x):
Answer: 2nd way
.
Let us apply the ideas of the method of intervals directly to the original inequality. For this, we recall that the expressions a b- a c and ( a - 1)(b- 1) have one sign. Then our inequality for x> 3 is equivalent to the inequality or The last inequality is solved by the interval method Answer: Example 3
Solution:
Apply the interval method Answer: Example 4
Solution:
Since 2 x 2 - 3x+ 3 > 0 for all real x, That To solve the second inequality, we use the interval method In the first inequality, we make the change then we arrive at the inequality 2y 2 - y - 1 < 0 и, применив метод интервалов, получаем, что решениями будут те y, which satisfy the inequality -0.5< y < 1.
From where, because we get the inequality which is carried out with x, for which 2 x 2 - 3x - 5 < 0. Вновь применим метод интервалов
Now, taking into account the solution of the second inequality of the system, we finally obtain Answer:
Example 5
Solution:
Inequality is equivalent to a set of systems or Apply the interval method or Answer:
Example 6
Solution:
Inequality is tantamount to a system Let Then y > 0,
and the first inequality system takes the form or, expanding square trinomial for multipliers, Applying the interval method to the last inequality, we see that its solutions satisfying the condition y> 0 will be all y > 4.
Thus, the original inequality is equivalent to the system: So, the solutions of the inequality are all 2.2. rationalization method. Earlier method rationalization of inequality was not solved, it was not known. This is the new modern effective method solutions of exponential and logarithmic inequalities" (quote from the book by Kolesnikova S.I.) "Magic Table"
In other sources
If a >1 and b >1, then log a b >0 and (a -1)(b -1)>0; If a >1 and 0 if 0<a<1 и b
>1, then log a b<0 и (a
-1)(b
-1)<0;
if 0<a<1 и 00 and (a -1)(b -1)>0. The above reasoning is simple, but noticeably simplifies the solution of logarithmic inequalities. Example 4
log x (x 2 -3)<0
Solution:
Example 5
log 2 x (2x 2 -4x +6)≤log 2 x (x 2 +x ) Solution: Example 6
To solve this inequality, we write (x-1-1) (x-1) instead of the denominator, and the product (x-1) (x-3-9 + x) instead of the numerator. Example 7
Example 8
2.3. Non-standard substitution. Example 1
Example 2
Example 3
Example 4
Example 5
Example 6
Example 7
log 4 (3 x -1) log 0.25 Let's make the substitution y=3 x -1; then this inequality takes the form log 4 log 0.25 Because log 0.25 Let's make a replacement t =log 4 y and get the inequality t 2 -2t +≥0, the solution of which is the intervals - Thus, to find the values of y, we have a set of two simplest inequalities Therefore, the original inequality is equivalent to the set of two exponential inequalities, The solution of the first inequality of this set is the interval 0<х≤1, решением второго – промежуток 2≤х<+ Example 8
Solution:
Inequality is tantamount to a system The solution of the second inequality, which determines the ODZ, will be the set of those x,
for which x > 0.
To solve the first inequality, we make the change Then we get the inequality or The set of solutions of the last inequality is found by the method intervals: -1< t < 2. Откуда, возвращаясь к переменной x, we get or Many of those x, which satisfy the last inequality belongs to ODZ ( x> 0), therefore, is a solution to the system, and hence the original inequality. Answer: 2.4. Tasks with traps. Example 1
Solution. The ODZ of the inequality is all x satisfying the condition 0 Example 2
log 2 (2x +1-x 2)>log 2 (2x-1 +1-x)+1. Conclusion
It was not easy to find special methods for solving C3 problems from a large variety of different educational sources. In the course of the work done, I was able to study non-standard methods for solving complex logarithmic inequalities. These are: equivalent transitions and the generalized method of intervals, the method of rationalization ,
non-standard substitution ,
tasks with traps on the ODZ. These methods are absent in the school curriculum. Using different methods, I solved 27 inequalities offered at the USE in part C, namely C3. These inequalities with solutions by methods formed the basis of the collection "Logarithmic C3 Inequalities with Solutions", which became the project product of my activity. The hypothesis I put forward at the beginning of the project was confirmed: C3 problems can be effectively solved if these methods are known. In addition, I discovered interesting facts about logarithms. It was interesting for me to do it. My project products will be useful for both students and teachers. Conclusions:
Thus, the goal of the project is achieved, the problem is solved. And I got the most complete and versatile experience in project activities at all stages of work. In the course of working on the project, my main developmental impact was on mental competence, activities related to logical mental operations, the development of creative competence, personal initiative, responsibility, perseverance, and activity. A guarantee of success when creating a research project for I have become: significant school experience, the ability to extract information from various sources, check its reliability, rank it according to its significance. In addition to directly subject knowledge in mathematics, he expanded his practical skills in the field of computer science, gained new knowledge and experience in the field of psychology, established contacts with classmates, and learned to cooperate with adults. In the course of project activities, organizational, intellectual and communicative general educational skills and abilities were developed. Literature
1. Koryanov A. G., Prokofiev A. A. Systems of inequalities with one variable (typical tasks C3). 2. Malkova A. G. Preparing for the Unified State Examination in Mathematics. 3. S. S. Samarova, Solution of logarithmic inequalities. 4. Mathematics. Collection of training works edited by A.L. Semyonov and I.V. Yashchenko. -M.: MTsNMO, 2009. - 72 p.-


Solution of examples
![]()



3x > 24;
x > 8. ![]()
What is needed to solve logarithmic inequalities?
Homework

\(\log_3 ((x^2-3))< \log_3{(2x)}\)
\(\log_(x+1)((x^2+3x-7))>2\)
\(\lg^2((x+1))+10≤11 \lg((x+1))\)How to solve logarithmic inequalities:
\(-\) if - a number and it is greater than 1 - the inequality sign remains the same during the transition,
\(-\) if the base is a number greater than 0 but less than 1 (between zero and one), then the inequality sign must be reversed, i.e.
ODZ: \(8-x>0\)
\(-x>-8\)
\(x<8\)
\(\log\)\(_2\) \((8-x)<\log\)\(_2\)
\({2}\)
\(8-x\)\(<\)
\(2\)
\(8-2
Answer: \((6;8)\)
ODZ: \(\begin(cases)2x-4>0\\x+1 > 0\end(cases)\)
\(\begin(cases)2x>4\\x > -1\end(cases)\) \(\Leftrightarrow\) \(\begin(cases)x>2\\x > -1\end(cases) \) \(\Leftrightarrow\) \(x\in(2;\infty)\)
\(2x-4\)\(≤\)\(x+1\)
\(2x-x≤4+1\)
\(x≤5\)
Answer: \((2;5]\)
Answer:
\(x∈(\)\(\frac(3)(2)\) \(;\)\(\frac(7)(3)]\)

\(x∈(\)\(\frac(3)(2)\) \(;\)\(\frac(7)(3)]\)

Answer:
\((0; \frac(1)(3))∪(9;∞)\)
\(t^2-t-2>0\) Expand the left side of the inequality into .
\(t_1= \frac(1+3)(2)=2\)
\(t_2=\frac(1-3)(2)=-1\)
\((t+1)(t-2)>0\)

 if a > 1
if a > 1 if 0 <
а <
1
if 0 <
а <
1

 , and 0 on the right.
, and 0 on the right. .
.
 , that is, solve the equation
, that is, solve the equation  (and solving an equation is usually easier than solving an inequality).
(and solving an equation is usually easier than solving an inequality). at the received intervals.
at the received intervals.


![]()

![]()
![]()











![]()



![]()





![]()

![]()
![]()
![]()


![]()
And even if the teacher knew him, there was a fear - but does the USE expert know him, and why don’t they give him at school? There were situations when the teacher said to the student: "Where did you get it? Sit down - 2."
Now the method is being promoted everywhere. And for experts, there are guidelines associated with this method, and in "The most complete editions of standard options ..." in solution C3, this method is used.
THE METHOD IS GREAT!






 Answer. (0; 0.5) U .
Answer. (0; 0.5) U .
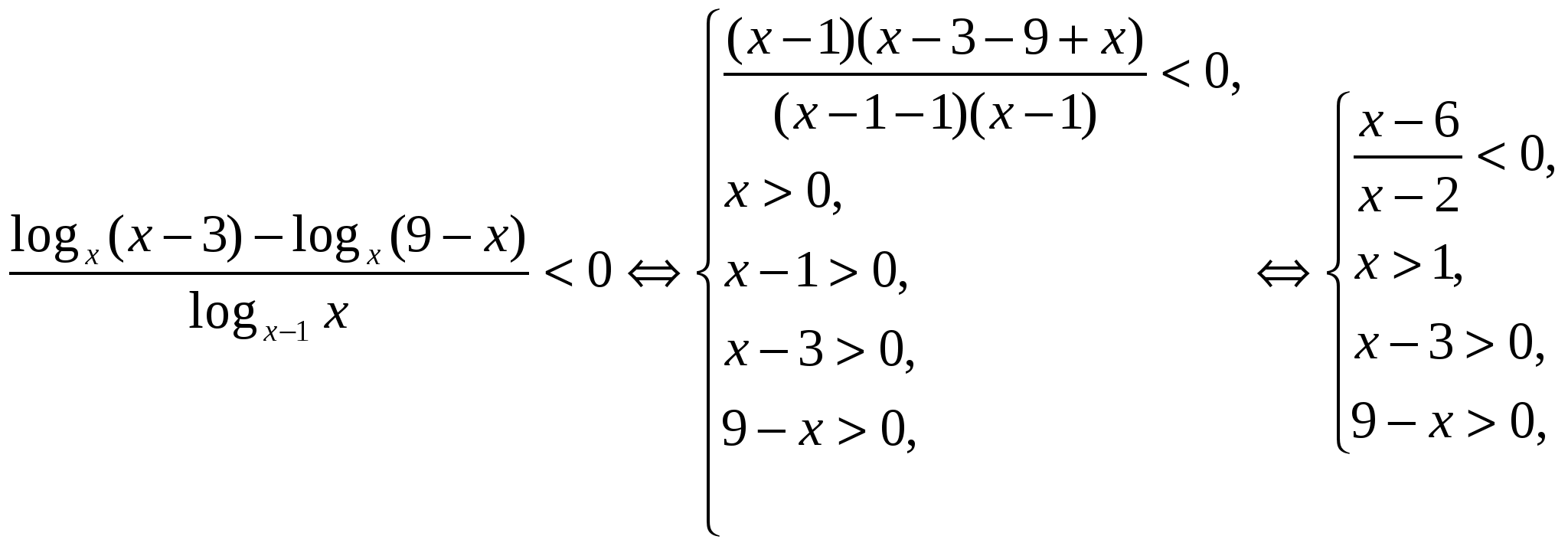

 Answer :
(3;6)
Answer :
(3;6)









 .
.
 = -log 4
= -log 4  = -(log 4 y -log 4 16)=2-log 4 y , then we rewrite the last inequality as 2log 4 y -log 4 2 y ≤.
= -(log 4 y -log 4 16)=2-log 4 y , then we rewrite the last inequality as 2log 4 y -log 4 2 y ≤.
 The solution of this collection is the intervals 0<у≤2 и 8≤у<+
The solution of this collection is the intervals 0<у≤2 и 8≤у<+ .
.
 that is, aggregates
that is, aggregates 
 . Thus, the original inequality holds for all values of x from the intervals 0<х≤1 и 2≤х<+
. Thus, the original inequality holds for all values of x from the intervals 0<х≤1 и 2≤х<+ .
.


![]()
![]()
![]()


 .
.
 . Therefore, all x from the interval 0
. Therefore, all x from the interval 0